摘要:针对集装箱港口提箱过程中的翻箱问题,以最小化翻箱次数为目标,构建基于状态结点的网络图模型,将翻箱问题转化为最短路径问题,并采用最短路径算法进行求解,最后给出一组计算样例。
1.集装箱堆场翻箱问题
在集装箱码头作业过程中,由于船舶抵港时间具有不确定性,可能出现集装箱提箱顺序与初始堆放位置不完全相符的情况,导致需要较早离场集装箱被压在后续离场集装箱下层现象。所以提箱过程中不可避免需要进行翻箱,甚至当被翻箱落箱位置选取不当,会造成后续提箱的二次翻箱;翻箱过程存在如下定义:
(1)目标箱:某一堆存状态下,预最先发箱的集装箱为该堆存状态下的目标箱;
(2)必翻箱:若某集装箱下方存在比其优先取箱的箱子,则该集装箱为相应堆存状态下的必翻箱;
(3)阻塞箱:连续堆存在某集装箱上方的必翻箱,为相应堆存状态下该集装箱的阻塞箱;
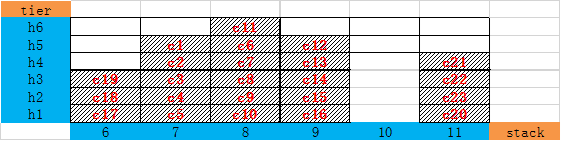
如图1所示为某一贝位内的堆存状态(6*6的贝位,且均为20FT集装箱,底部横轴为栈编号,左侧纵轴为层编号);当提箱顺序为C21->C15->C12时,可知当前堆存状态的目标箱位C21,C12处于栈顶,不存在阻塞箱,可直接发出;而C15作为后续堆存状态的目标箱,其上方还有其他集装箱;此时,定义C12,C13,C14为目标箱C15的阻塞箱,同时C12,C13,C14称为当前堆存状态的必翻箱;
图1 堆存状态
2. 基于状态结点的网络图模型
(1)堆存状态:指某堆存范围内集装箱的堆存情况,如图1所示,即为栈6-11的一组堆存状态;翻箱过程中可行的堆存状态应具有如下特点:
a):集装箱不能悬空放置;
b):不考虑轻压重等重量原则;
c):不允许超过堆存区域既定的最大堆高;
d):集装箱位置不能超过作业机械所能达到的最大堆高;
(2)状态结点:每一个可行的堆存状态即可作为一个状态结点;
(3)结点可达:针对某一目标箱,若状态结点A中的某一集装箱经过翻箱操作后得到的堆存状态与状态结点B一致,则称结点A可达结点B;
(4)权重取值: 且若结点A可达结点B,那么结点A、B间存在方向A->B,且可计算A->B的翻箱次数,并将其作为连接权重;
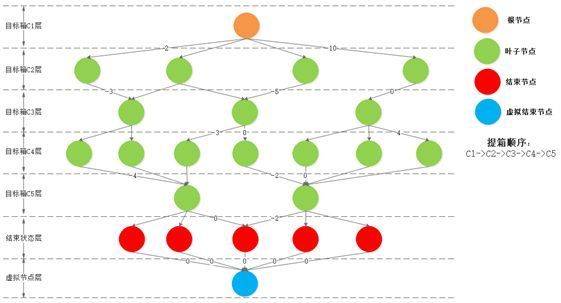
(5)网络图构建原理:以初始堆存状态作为根节点,将目标箱作为层级划分的标识。同时,将提箱过程中各层可能的堆存状态作为该层的叶子节点,完成提箱操作的堆存状态作为结束节点;构造形如图2所示的树状网络图结构,并增加虚拟结束节点:
图2状态结点树状网络图
(4)网络图性质:分析可知,上述构造的堆存状态树状网络图具有以下特征:
特征0:结束状态层中,不存在待提集装箱,此时堆存状态可能为空,也可能包括非待提箱;
特征1:图中入度为0的点和出度为0的点有且仅有一个(分别为根节点和虚拟结束节点);其他节点的出度、入度均大于等于1;
特征2:虚拟节点作为后续节点与所有结束节点相连,且权重均等于0;
特征3:上一层的目标箱在当前堆存状态一定处于栈顶或已被提箱离场;
特征4:由于提箱顺序有优先级要求,结合特征3,因此不存在跨层节点连接;
特征5:由于不涉及预翻箱作业,则中间层每层至少存在一个状态叶子节点,且两两状态之间不可达;
特征6:结合特征4和特征5可知,网络图为有向无环图;
至此,通过构建具有上述特征的树状网络图,可将翻箱问题转化为寻找从根节点到虚拟结束节点的最短路径问题,并采用最短路径问题算法进行精确求解。
3. 计算样例
(1)初始堆存状态Node0;
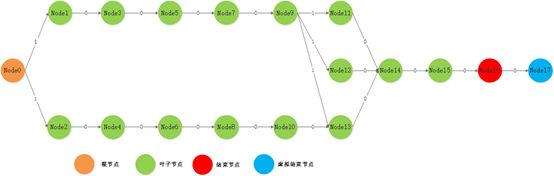
(2)构造树型网络图结构
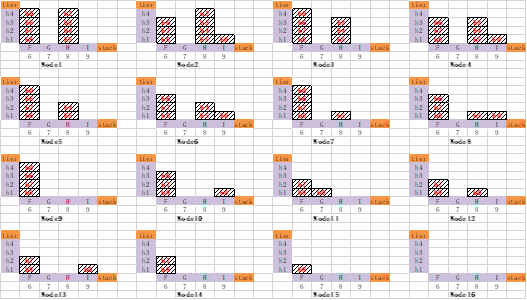
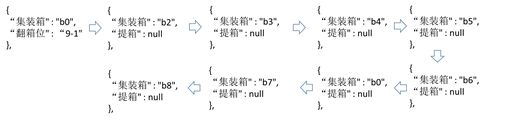
结点信息如下:
(3)最短路径问题求解
当前最短路径支持Dijkstra's 算法(正权有向图)、Floyd算法、0-1整数规划等方式求解;此外,进一步结合特征6可知,上述构建的最短路径问题为有向无环图,因此可采用更为高效的基于拓扑排序的快速求解算法求解;最终得到翻箱方案如下,翻箱次数为1次;
参考文档
- da Silva Firmino A, de Abreu Silva R M, Times V C. An exact approach for the container retrieval problem to reduce crane's trajectory[C]//2016 IEEE 19th international conference on intelligent transportation systems (ITSC). IEEE, 2016: 933-938.
- https://bbs.huaweicloud.com/blogs/211445-有向无环图最短路径问题及其变种问题的快速求解算法.
本文分享自华为云社区《集装箱港口翻箱问题的最短路径求解算法》,原文作者:CKW@10270 。