RRT算法在三维轨迹规划中的MATLAB仿真

RRT二维轨迹规划

关于RRT二维轨迹规划以及matlab实现参考博客：
RRT

RRT算法简单思路分析

1. 生成根节点，并给出终止节点。
2. 随机在空间中找到一点$r$(50%随机点，50%为目标点)，判断$r$与轨迹树中哪一个节点的欧氏距离最小，记该节点为$nod{e}_{best}$。
3. 从$nod{e}_{best}向$$r$延伸步长$stepSize$个单位（用向量实现）。
4. 判断线段$nod{e}_{best}->r$是否触碰到障碍物。若是，放弃该$r$，回到2。
5. 判断$r$是否临近目标点，若是，退出循环，否则将$r$添加到轨迹树，回到2。

算法还可以引入最大错误次数，若在一个迭代过程中超过最大错误次数依旧没有找到不发生碰撞的新子节点，则退出循环，并error一个“无法找到合理轨迹”。

RRT优势与劣势

通过对状态空间中的采样点进行碰撞检测，避免了对空间的建模，能够有效地解决高维空间和复杂约束的路径规划问题。该方法的特点是能够快速有效地搜索高维空间，通过状态空间的随机采样点，把搜索导向空白区域，从而寻找到一条从起始点到目标点的规划路径，适合解决多自由度机器人在复杂环境下和动态环境中的路径规划。与PRM类似，该方法是概率完备且不最优的。

三维轨迹规划MATLAB仿真

二维的见上面给出的博客。
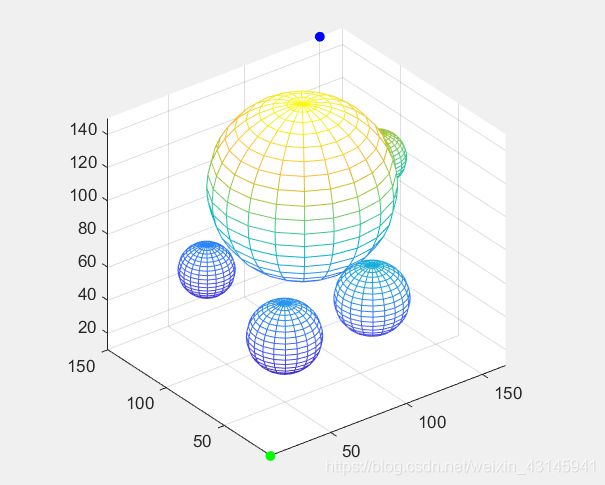
我们将三维障碍物设定为球，这样方便碰撞检测和绘图。

%% 绘制障碍物(以球为例，主要是方便计算)
x0=100; y0=100; z0=100;%球心
circleCenter = [100,100,100;50,50,50;100,40,60;150,100,100;60,130,50];
r=[50;20;20;15;15];%半径
%下面开始画
figure(1);
[x,y,z]=sphere;
for i = 1:length(circleCenter(:,1))
    mesh(r(i)*x+circleCenter(i,1),r(i)*y+circleCenter(i,2),r(i)*z+circleCenter(i,3));hold on;
end
axis equal

把球心和对应的半径填入 circleCenter 和 r 矩阵即可。

给定仿真参数：
goal为目标
source为起始

%% 参数
source=[10 10 10];
goal=[150 150 150];
stepsize = 10;
threshold = 10;
maxFailedAttempts = 10000;
display = true;
searchSize = [250 250 250];      %探索空间六面体

这里的探索空间六面体为随机点所在的空间。

绘制起始点和终止点：

%% 绘制起点和终点
hold on;
scatter3(source(1),source(2),source(3),"filled","g");
scatter3(goal(1),goal(2),goal(3),"filled","b");

主循环：
failedAttempts为最大错误次数，pathFound为是否找到规划路径，RRTree为生成树。

tic;  % tic-toc: Functions for Elapsed Time
RRTree = double([source -1]);
failedAttempts = 0;
pathFound = false;

%% 循环
while failedAttempts <= maxFailedAttempts  % loop to grow RRTs
    %% chooses a random configuration
    if rand < 0.5
        sample = rand(1,3) .* searchSize;   % random sample
    else
        sample = goal; % sample taken as goal to bias tree generation to goal
    end
    %% selects the node in the RRT tree that is closest to qrand
    [A, I] = min( distanceCost(RRTree(:,1:3),sample) ,[],1); % find the minimum value of each column
    closestNode = RRTree(I(1),1:3);
    %% moving from qnearest an incremental distance in the direction of qrand
    movingVec = [sample(1)-closestNode(1),sample(2)-closestNode(2),sample(3)-closestNode(3)];
    movingVec = movingVec/sqrt(sum(movingVec.^2));  %单位化
    newPoint = closestNode + stepsize * movingVec;
    if ~checkPath3(closestNode, newPoint, circleCenter,r) % if extension of closest node in tree to the new point is feasible
        failedAttempts = failedAttempts + 1;
        continue;
    end
    
    if distanceCost(newPoint,goal) < threshold, pathFound = true; break; end % goal reached
    [A, I2] = min( distanceCost(RRTree(:,1:3),newPoint) ,[],1); % check if new node is not already pre-existing in the tree
    if distanceCost(newPoint,RRTree(I2(1),1:3)) < threshold, failedAttempts = failedAttempts + 1; continue; end 
    
    RRTree = [RRTree; newPoint I(1)]; % add node
    failedAttempts = 0;
    if display, plot3([closestNode(1);newPoint(1)],[closestNode(2);newPoint(2)],[closestNode(3);newPoint(3)],'LineWidth',1); end
    pause(0.05);
end

if display && pathFound, plot3([closestNode(1);goal(1)],[closestNode(2);goal(2)],[closestNode(3);goal(3)]); end

if display, disp('click/press any key'); waitforbuttonpress; end
if ~pathFound, error('no path found. maximum attempts reached'); end

回溯规划轨迹：

%% retrieve path from parent information
path = goal;
prev = I(1);
while prev > 0
    path = [RRTree(prev,1:3); path];
    prev = RRTree(prev,4);
end

pathLength = 0;
for i=1:length(path(:,1))-1, pathLength = pathLength + distanceCost(path(i,1:3),path(i+1,1:3)); end % calculate path length
fprintf('processing time=%d \nPath Length=%d \n\n', toc, pathLength); 
figure(2)
for i = 1:length(circleCenter(:,1))
    mesh(r(i)*x+circleCenter(i,1),r(i)*y+circleCenter(i,2),r(i)*z+circleCenter(i,3));hold on;
end
axis equal
hold on;
scatter3(source(1),source(2),source(3),"filled","g");
scatter3(goal(1),goal(2),goal(3),"filled","b");
plot3(path(:,1),path(:,2),path(:,3),'LineWidth',2,'color','r');

运行（还有三个碰撞检测函数的代码放在后面给出）：

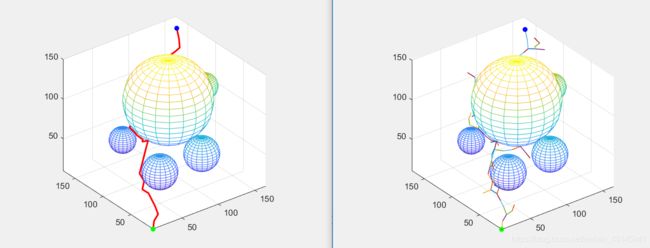
GIF:

命令行打印出时间和路径长：

碰撞检测函数代码

%% checkPath3.m	
function feasible=checkPath3(n,newPos,circleCenter,r)
feasible=true;
movingVec = [newPos(1)-n(1),newPos(2)-n(2),newPos(3)-n(3)];
movingVec = movingVec/sqrt(sum(movingVec.^2)); %单位化
for R=0:0.5:sqrt(sum((n-newPos).^2))
    posCheck=n + R .* movingVec;
    if ~(feasiblePoint3(ceil(posCheck),circleCenter,r) && feasiblePoint3(floor(posCheck),circleCenter,r))
        feasible=false;break;
    end
end
if ~feasiblePoint3(newPos,circleCenter,r), feasible=false; end
end

function h=distanceCost3(a,b)         %% distanceCost.m
	h = sqrt(sum((a-b).^2, 2));
end

%% feasiblePoint3.m
function feasible=feasiblePoint3(point,circleCenter,r)
feasible=true;
% check if collission-free spot and inside maps
for row = 1:length(circleCenter(:,1))
    if sqrt(sum((circleCenter(row,:)-point).^2)) <= r(row)
        feasible = false;break;
    end
end
end

二维规划的补充

利用visio绘制几张障碍图，二值化，使用推荐的博客代码运行：

可以看到RRT算法得到的轨迹不够平滑，可以改进，采用多项式拟合技术，这里就不再深入了，有兴趣的可以与作者讨论。