随机变量生成
这部分包括:
- 采用R语言内建函数的方法;
- 采用基于变换(transformation)的方法;
- 采用接受-拒绝(accept-reject)的方法;
基于R内建函数
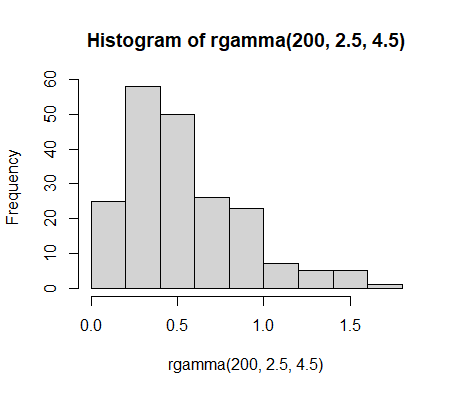
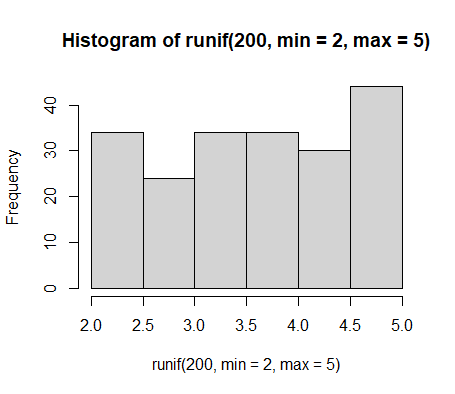
hist(rgamma(200,2.5,4.5)) #按照gamma(2.5,4.5)生成100个样本点并画出hist直方图hist(runif(200,min=2,max=5) )#按照在区间[2,5]上的均匀分布生成200个样本点并画出hist直方图其他一些常见的R语言内建分布如下:
- 高斯分布:rnorm(n,mean=0,std=1)
- 指数分布:rexp(n,rate=1)
- 泊松分布:rpois(n,lambda)
- Weibull分布:rweibull(n,shape,scale=1)
- 柯西分布:rcauchy(n,location=0,scale=1)
- Beta分布:rbeta(n,shape1.shape2)
- t分布:rt(n,df)
- F分布:rf(n,df1,df2)
- 卡方分布:rchisq(n,df)
- 二项分布:rbinom(n,size,prob)
- 超几何分布:rhyper(nn,m,n,k)
- Logistic分布:rlogis(n,location=0,scale=1)
- 负二项分布:rnbinom(n,size,prob)
- Wilcoxon分布:rwilcox(nn,m,n)
- 对数正态分布:rlnorm(n,meanlog=0,sdlog=1)
基于变换(transformation)
基于变换的方法指的是采用先按照简单的容易生成的分布生成样本点,然后利用某种变换关系将服从简单分布的样本服从满足复杂分布的样本。比如先采用R内建函数runif生成100个[0,1]均匀分布的样本点,然后利用变换将其变为服从较复杂的指数分布的样本点。
逆变换法(inverse transformation)
这种方法的流程如下所示:
- 获得想要生成的分布的累积分布函数F(x)并推导出其反函数$F^{-1}(x)$;
- 利用内建函数生成大量服从均匀分布U(0,1)的样本点;
- 对上一步生成的样本点进行$F^{-1}(x)$变换,其结果可以被认为是服从想要生成的F(x)分布。
为了理解这种方法的原理,首先给出如下定理:
若X是一个连续随机变量,其累积分布函数为F(x),则$U=F(x)\sim U(0,1)$。
这个定理可以简单理解如下:累积分布函数F(x)是把一切X的取值一对一地映射到[0,1]区间上。离散来看,可以认为F(x)在数轴[0,1]上每个点均有一个样本,因此“线密度”是均匀的。如果对于$U=F(x)∈[0,1]$进行抽样,抽中每个值的概率均等,因此U=F(x)服从U(0,1)。
文献(Introduction to probability and mathematical statistics / Lee J. Bain, Max Engelhardt)对上面定理给出了如下一个比较严格的证明:
$$ \begin{aligned} F_{u}(U) &=P(U \leq u) \\ &=P(F(X) \leq u)\\ &=P(F^{-1}(F^{}(X)) \leq F^{-1}(u))\\ &=P(X \leq F^{-1}(u))\\ &=F(F^{-1}(u))\\ &=u \end{aligned} $$
因为$F_{u}(U)∈[0,1]$且$F_{u}(U)=u$,显然$U$服从U(0,1)
如果直接利用内建函数生成了$u \sim U(0,1)$,则$F^{-1}(u)$和X同分布可以证明如下:
$$ \begin{aligned} F_{u}(U) &=P(U \leq u) \\ &=P(F^{-1}(X) \leq F^{-1}(x))\\ &=P(F^{}(F^{-1}(X)) \leq F^{}(F^{-1}(x)))\\ &=P(X \leq x) \end{aligned} $$
上式中第一个等号是根据累积分布函数的定义,第二个等号是根据上文关于F(x)的定理,第三个等号是因为F(x)是单调增函数。
实验:利用逆变换方法生成指数分布
指数分布的CDF为$F(x)=1-e^{-x}$,CDF的反函数为$x=-ln(1-F(x))$。R代码如下:
> N=10000 #样本数量
> U=runif(N) #生成的U(0,1)样本
> X=-log(1-U) #进行逆变换
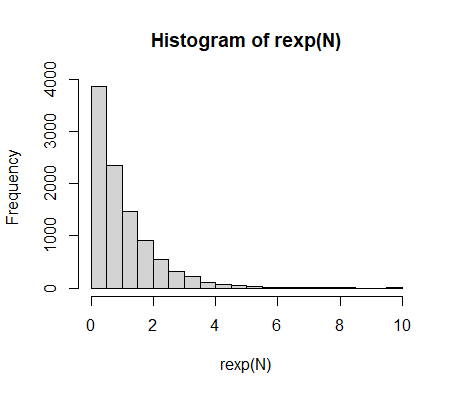
> hist(X) #画出直方图
> hist(rexp(N)) #画出R内建的指数分布直方图其他基于变换的方法
当$X \sim exp(1)$时,可以根据如下公式生成几种常见的分布:
$$ Y=2\sum_{j=1}^{\nu}X_{j} \sim \chi_{2 \nu }^2 \qquad \nu\in\mathbb{N}^{*}\\ Y=\beta\sum_{j=1}^{\alpha}X_{j} \sim \Gamma(\alpha,\beta) \qquad \alpha\in\mathbb{N}^{*}\\ Y=\frac{\sum_{j=1}^{a}X_{j}}{\sum_{j=1}^{a+b}X_{j}} \sim \beta(a,b) \qquad a,b\in\mathbb{N}^{*}\\ $$
Box-Muller算法可以用于生成正态分布,按照以下公式生成的$X_{1}$和$X_{2}$为相互独立的正态分布:
$$ U_{1},U_{2} \sim U(0,1)\\ X_{1}=\sqrt{-2log(U_{1})}cos(2 \pi U_{2})\\ X_{2}=\sqrt{-2log(U_{1})}sin(2 \pi U_{2})\\ $$
混合方法(Mxiture representations)
混合方法指的是按照下式生成概率密度分布$f(x)$的方法:
$$ f(x)=\int_{\gamma}g(x|y)p(y)dy $$
其中$p(y)$和$g(x|y)$均为容易生成的分布。
使用混合方法时,先生成$p(y)$再生成$g(x|y)$,就能够得到$X \sim f(x)$。
实验:采用混合方法生成$X\sim \mathcal{N}eg(6,0.3)$
根据相关理论,$X\sim \mathcal{N}eg(n,p)$可以分解为如下两个分布:
$$ Y \sim \Gamma(n,(1-p)/p)\\ X|y \sim \mathcal{P}(y) $$
按照上式生成X并与R内建函数进行对比的代码如下:
> N=10000
> n=6;p=0.3
> y=rgamma(N,n,rate=p/(1-p))
> x=rpois(N,y)
> par(mfcol=c(1,2))
> hist(x)
> hist(rnbinom(N,n,p))实验结果如下图所示,可以看出按照混合方法生成的样本点和内建函数生成$X\sim \mathcal{N}eg(6,0.3)$的分布非常接近。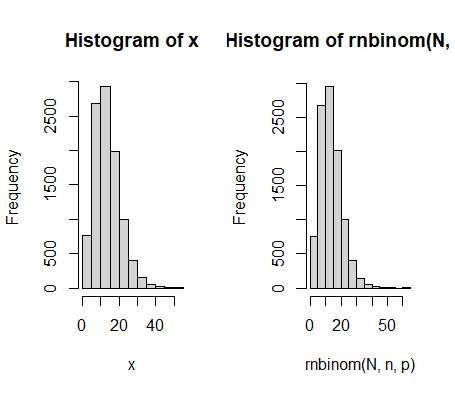
接受-拒绝算法(accept-reject algorithm)
当已经获取想要生成的分布的概率密度分布$f(x)$(称为目标分布,target density)时,还有一种通过简单分布$g(x)$(称为提议分布,candidate density)生成复杂分布的方法:接受-拒绝算法。应用这种算法前必须按照如下步骤先确定$g(x)$和常数M:
- 根据$f(x)$的固有特性,确定一个满足如下条件的$g(x)$:
(1)$g(x)$必须足够容易和方便生成;
(2)当$g(x)>0$时,$f(x)>0$;
(3)存在常数M,使得$M \ge \frac{f(x)}{g(x)}$对任意x均成立;
- 利用数学原理或者数值优化算法得到符合要求的常数M
当$g(x)$和M已经确定后,根据如下步骤生成$X \sim f(x)$:
- 生成N个提议分布$y\sim g(y)$的样本点$Y_{N}$和均匀分布$u\sim U(0,1)$的样本点$U_{N}$;
- 对每个$n\leq N$,当$U_{n} \leq \frac{f(Y_{n})}{Mg(Y_{n})}$时,接受$Y_{n}$作为生成的X样本点,否则拒绝$Y_{n}$。
说明这个算法的有效性等于要证明$f_{y}(y|accepted)=f_{x}(y)$,证明如下:
$$ \begin{aligned} f_{y}(y|accepted) &=\frac{f_{y,accetped}(y,accetped)}{P(accepted)} \\ &=\frac{f_{y,accetped}(y,accepted)}{\int_{y}{f_{accetped}(accetped|y)}f_{y}(y)}\\ &=\frac{g(y) \frac{f_x(y)}{Mg(y)}}{\int_{y}{\frac{f_{x}(y)}{Mg(y)}g(y)dy}}\\ &=\frac{\frac{1}{M}f_{x}(y)}{\frac{1}{M}}\\ &=f_{x}(y) \end{aligned} $$
上述证明中$f_{y}(y)=g(y)$,$f_{x}(y)$其实就是想要生成的$f(x)$,第二个等号处利用了贝叶斯定理。
从上述证明中还可以看出:
$$ \begin{aligned} P(accepted) &=\int_{y}{f_{accetped}(accetped|y)}f_{y}(y) \\ &=\frac{1}{M} \end{aligned} $$
因此,在接受-拒绝算法中如果一次性生成了N个提议分布的样本点,最终能够被接受为X的大约有$\frac{N}{M}$个样本点。
实验:接受-拒绝算法生成$X \sim \beta(2.7,6.3)$
应用接受-拒绝算法生成$X \sim \beta(2.7,6.3)$,采用$y \sim U(0,1)$作为提议分布,在已知$\beta(2.7,6.3)$的概率密度函数情况下,利用优化算法得到M值为2.67。R语言代码如下:
> M=2.67
> N=10000
> u=runif(N,max = M)
> y=runif(N) #生成提议分布
> x=y[u par(mfcol=c(1,2))
> hist(x)
> hist(rbeta(10000,2.7,6.3)) 实验结果如下图所示,可以看出按照接受-拒绝算法生成的样本点和内建函数生成$X \sim \beta(2.7,6.3)$的分布非常接近。另外,生成的X样本点共有3824个,接受率为38.2%,和理论接受率$\frac{1}{M}$即37%十分接近。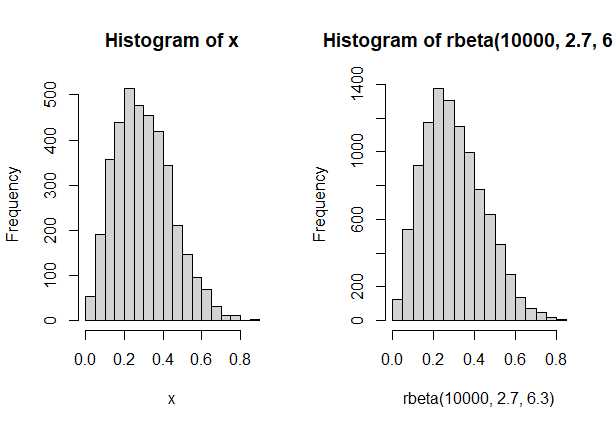
接受-拒绝算法的优化
对于接受-拒绝算法,核心性能指标就是计算效率,即在单位时间内能够生成的$X \sim f(x)$样本点的个数。上文已经提到,接受概率约为$\frac{1}{M}$,当生成N个提议分布的样本点时约$\frac{N}{M}$个被接受。因此,提高接受-拒绝算法的性能可以从两方面下手:
- 提高N,选择效率高的提议分布生成算法;
- 降低M,通过优化算法查找能够满足要求的M最小值,同时也可以将提议分布的搜索限定在某种能够高效生成的分布族里,以最小化M为目标对分布族的参数进行优化计算,最终求得效率最高的提议分布。
- 对以上两点进行平衡,因为第二点中求得的最优提议分布的生成效率可能较低。