剑指offer-leetcode-最大最小问题-思路篇

接

https://blog.csdn.net/MaYingColdPlay/article/details/105905939

字符串问题用动态规划

二叉树路径问题用回溯法

1.无重复字符最长子串

双指针法，用一个left指针，指向最左边，一个cur指针，指向当前，记录两者之间的距离。

用一个列表来记录当前无重复字符。如果有重复的子串，移动left指针。

不用两个指针也可，直接用一个list来判断就行了。list+从左边pop出当前存在的。

2.最小路径和

思路:

拿例子来说，dp[2][2]=min(dp[2][1],dp[1][2])+grid[2][2]，其中等式右边的dp也都是这么求的。

dp[1][2]=min(dp[1][1],dp[0][2])+grid[1][2]  ...动态规划数学方程。

首先对dp赋初始值，初始值就是i=0和j=0的时候。

 

3.最长回文子串

思路:用一个dp来表示从i到j是否为回文子串，首先初始化，dp[i][i]是True。

然后从index为1开始进行遍历，如果s[i]==s[j]，分两种情况，如果是两个挨着的，是True，

如果不是挨着的，等于他上一个状态。

判断是否为最大值，如果是最大值，记录当前的下标i和max_len，从s中进行索引。

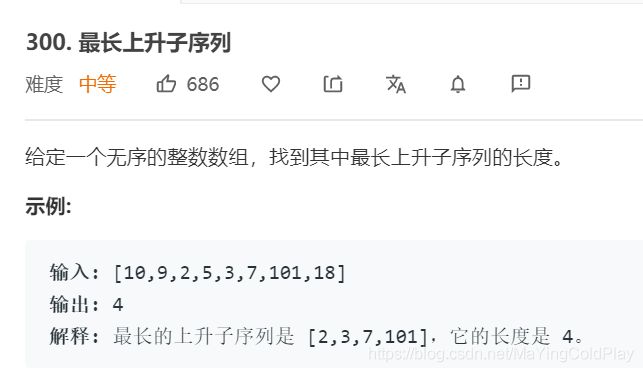
4.最长上升子序列

思路:动态规划，dp[i]表示到位置i时的最长上升子序列，从0遍历到i，如果nums[i]大于nums[j],

dp[i]=dp[j]+1,注意要选择dp[i]与dp[j]+1的最大值。

5.最大子序和

dp[i]表示到i为止的连续子数组最大值。dp[i]=等于max(dp[i-1]+nums[i],num[i])

 

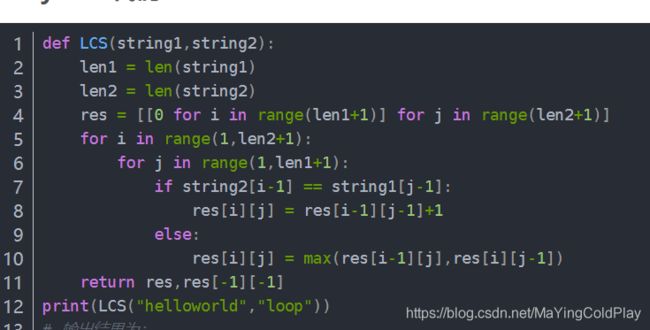
6.最长公共子序列

https://blog.csdn.net/ggdhs/article/details/90713154

在写代码的时候，为了赋初值方便，dp矩阵多增加一维，从字符串前面一位开始算。

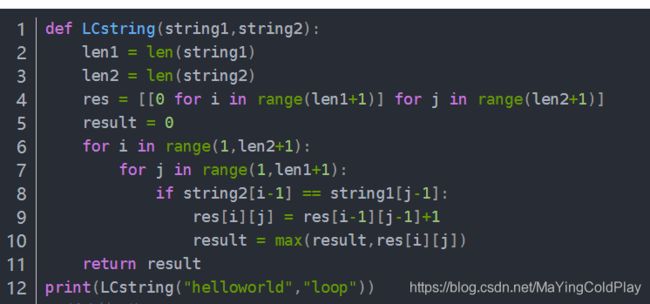
7.最长公共子串

8.二叉搜索树的最近公共祖先

https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof/solution/mian-shi-ti-68-i-er-cha-sou-suo-shu-de-zui-jin-g-7/

9.二叉树的最近公共祖先

9.1递归

https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof/solution/mian-shi-ti-68-ii-er-cha-shu-de-zui-jin-gong-gon-7/

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    #回溯,传入参数是root,path,如果root.val等于节点值，就把路径加入结果中。
    def dfs(self,root,path,res,target):
        path.append(root)
        if root.val==target:
            res.append(list(path))
        if root.left:
            self.dfs(root.left,path,res,target)
        if root.right:
            self.dfs(root.right,path,res,target)
        path.pop()
        return res
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        #找到两个节点的路径，然后取第一个交点。
        path1=[]
        path2=[]
        res1=[]
        res2=[]
        res1=self.dfs(root,path1,res1,p.val)[0]
        res2=self.dfs(root,path2,res2,q.val)[0]
        index1=0
        index2=0
        while index1<=len(res1)-2 and index2<=len(res2)-2:
            if res1[index1+1]!=res2[index2+1]:
                return res1[index1]
            else:
                index1=index1+1
                index2=index2+1
        if index1==len(res1)-1 and index2

9.2 非递归

https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/solution/xiong-mao-shua-ti-python3-hui-su-2tiao-lu-jing-sha/

回溯

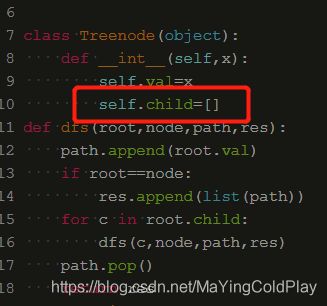
扩展：多叉树的情况

在类里面用一个list来保存多个子节点。

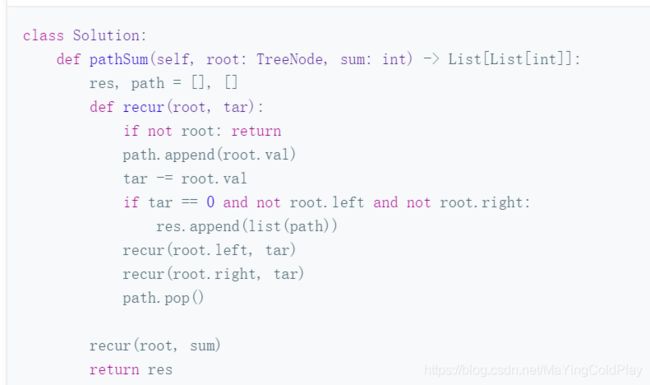
面试题34. 二叉树中和为某一值的路径

https://leetcode-cn.com/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof/solution/mian-shi-ti-34-er-cha-shu-zhong-he-wei-mou-yi-zh-5/

# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):
    #回溯，传入参数为root,res,target(根节点，保存结果的list,sum减去root.val)
    def __init__(self):
        self.res=[]
    def dfs(self,root,target,path):
        if not root:
            return 
        path.append(root.val)
        if target==root.val and not root.left and not root.right:
            self.res.append(list(path))
        if root.left:
            self.dfs(root.left,target-root.val,path)
        if root.right:
            self.dfs(root.right,target-root.val,path)
        path.pop()
    def pathSum(self, root, sum):
        """
        :type root: TreeNode
        :type sum: int
        :rtype: List[List[int]]
        """
        path=[]
        self.dfs(root,sum,path)
        return self.res

if __name__=="__main__":
    #构造二叉树
    n1=TreeNode(5)
    n21=TreeNode(4)
    n22=TreeNode(8)
    n31=TreeNode(11)
    n32=TreeNode(13)
    n33=TreeNode(4)
    n41=TreeNode(7)
    n42=TreeNode(2)
    n43=TreeNode(5)
    n44=TreeNode(1)
    n1.left=n21
    n1.right=n22
    n21.left=n31
    n22.left=n32
    n22.right=n33
    n31.left=n41
    n31.right=n42
    n33.left=n43
    n33.right=n44
    result=Solution().pathSum(n1,22)
    print(result)