机器学习----聚类分析(Kmeans聚类算法)
- 一、什么是聚类分析
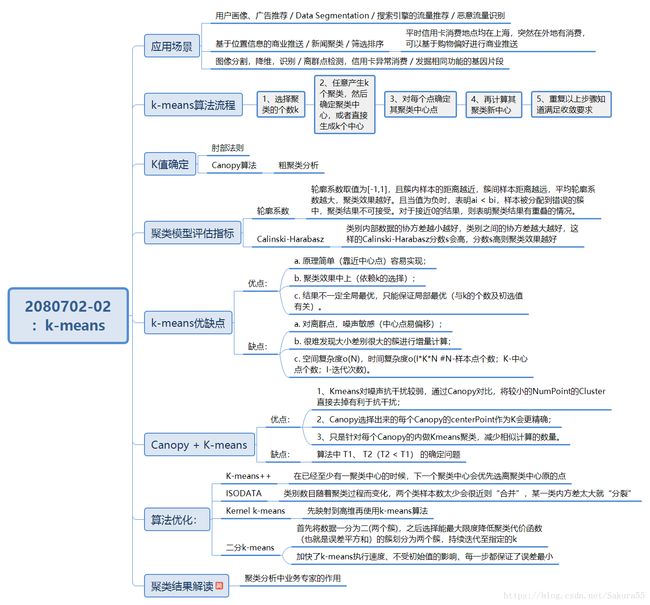
- 二、算法流程
- 三、优缺点
- 四、K值确定
-
- 4.1、肘部法则
- 4.2、肘部法则代码部分
-
- 五、算法效果衡量标准
-
- 5.1、轮廓系数
- 5.2、最近簇
- 5.3、轮廓系数法代码如下
- 5.4、Canopy算法配合初始聚类
- 5.5、优点
- 5.6、Calinski-Harabasz Index
-
- 六、算法优化
-
- 6.1、K-means++
- 6.2、映射到高维(Kernel k-means)
- 6.3、二分法(二分K-means)
- 6.4、Mini Batch K-Means
- 6.5、迭代自组织数据分析算法(ISODATA)
- 6.6、MCMC采样
- 6.7、AFK-MC^2
-
- 七、Sklearn实现
- 八、案例(图像压缩)
- 九、代码链接
一、什么是聚类分析
物以类聚,人以群分
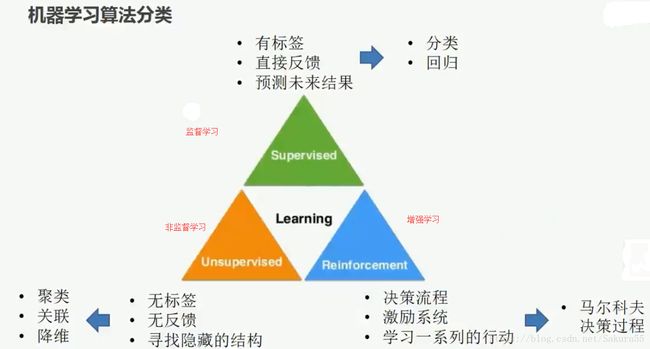
一种典型的无监督学习算法,主要用于将相似的样本自动归到一个类别中。
聚类算法与分类算法最大的区别是:聚类算法是无监督的学习算法,而分类算法属于监督的学习
算法。
在聚类算法中根据样本之间的相似性,将样本划分到不同的类别中,对于不同的相似度计算方法,会得到不同的聚类结果,常用的相似度计算方法有欧式距离法。
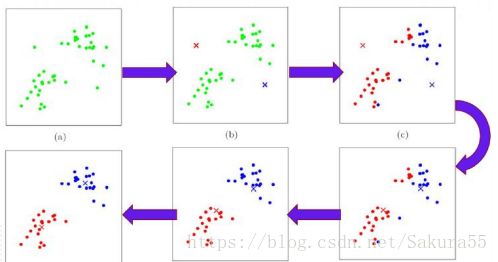
二、算法流程
1.选择聚类的个数k. 2.任意产生k个聚类,然后确定聚类中心,或者直接生成k个中心。
3.对每个点确定其聚类中心点。
4.再计算其聚类新中心。
5.重复以上步骤直到满足收敛要求。(通常就是确定的中心点不再改变。)
三、优缺点
四、K值确定
4.1、肘部法则
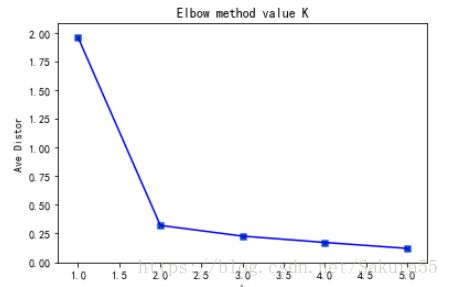
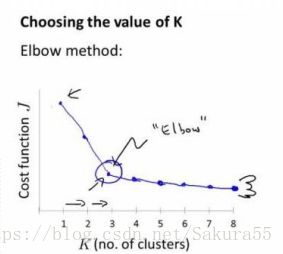
Elbow method就是“肘”方法,对于n个点的数据集,迭代计算k from 1 to n,每次聚类完成后计算每个点到其所属的簇中心的距离的平方和,可以想象到这个平方和是会逐渐变小的,直到k==n时平方和为0,因为每个点都是它所在的簇中心本身。但是在这个平方和变化过程中,会出现一个拐点也即“肘”点,下图可以看到下降率突然变缓时即认为是最佳的k值。
肘方法的核心指标是SSE(sum of the squared errors,误差平方和),Ci是第i个簇,p是Ci中的样本点,mi是Ci的质心(Ci中所有样本的均值),SSE是所有样本的聚类误差,代表了聚类效果的好坏。
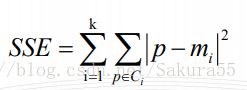
肘方法的核心思想:随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。并且,当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数。这也是该方法被称为肘方法的原因。
4.2、肘部法则代码部分
#K值的确定
import numpy as np
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']= ['SimHei'] #中文注释
plt.rcParams['axes.unicode_minus'] = False #显示正负号
cluster1 = np.random.uniform(0.5,1.5,(2,5))
cluster2 = np.random.uniform(3.5,4.5,(2,5))
X = np.hstack((cluster1,cluster2)).T
# print(X)
K = range(1, 6)
meandistortions = []
for k in K:
kmeans = KMeans(n_clusters=k)
# print(kmeans)
kmeans.fit(X)
# print(X.shape[0])
#找中"心位置,找出每个点到中心点的最小距离,求和,在求平均
###euclidean,欧式距离,固定的写法
meandistortions.append(sum(np.min(cdist(X,kmeans.cluster_centers_,'euclidean'), axis=1)) / X.shape[0])
print("#"*40+"第"+str(k)+"次测试")
print(cdist(X,kmeans.cluster_centers_,'euclidean'))
print("#"*40+"最小值")
print(np.min(cdist(X,kmeans.cluster_centers_,'euclidean'), axis=1))
print(meandistortions)
plt.plot(K, meandistortions,'bx-')
plt.xlabel('k')
# plt.ylabel('平均畸变程度',fontproperties=font)
plt.ylabel('Ave Distor')
# plt.title('用肘部法则来确定最佳的K值',fontproperties=font);
plt.title('Elbow method value K')
plt.scatter(K,meandistortions)
plt.show()>`运行结果如下:`
>########################################第1次测试
[[2.25689903]
[1.91540479]
[1.6724617 ]
[1.65759221]
[2.29541546]
[2.2529662 ]
[2.233567 ]
[1.7942795 ]
[1.90631309]
[1.59251126]]
>########################################最小值
[2.25689903 1.91540479 1.6724617 1.65759221 2.29541546 2.2529662
2.233567 1.7942795 1.90631309 1.59251126]
>########################################第2次测试
[[0.32754273 4.20172309]
[0.45410769 3.8348288 ]
[0.30422595 3.6161136 ]
[0.29081031 3.60350218]
[0.38598195 4.23833185]
[4.18875711 0.42497288]
[4.1691721 0.41257945]
[3.74022813 0.15539011]
[3.85181965 0.07822596]
[3.53695433 0.36974717]]
>########################################最小值
[0.32754273 0.45410769 0.30422595 0.29081031 0.38598195 0.42497288
0.41257945 0.15539011 0.07822596 0.36974717]
>########################################第3次测试
[[0.03759658 4.20172309 0.56450362]
[0.718618 3.8348288 0.37445254]
[0.60378679 3.6161136 0.22807088]
[0.6240233 3.60350218 0.14881965]
[0.03759658 4.23833185 0.62302545]
[4.50532033 0.42497288 3.98141545]
[4.50602853 0.41257945 3.94646646]
[4.0668868 0.15539011 3.52561081]
[4.17719886 0.07822596 3.63808518]
[3.86843718 0.36974717 3.31878573]]
>########################################最小值
[0.03759658 0.37445254 0.22807088 0.14881965 0.03759658 0.42497288
0.41257945 0.15539011 0.07822596 0.36974717]
>########################################第4次测试
[[0.56450362 4.13413228 0.03759658 4.48563964]
[0.37445254 3.77922358 0.718618 4.0758083 ]
[0.22807088 3.54804701 0.60378679 3.90379492]
[0.14881965 3.5373922 0.6240233 3.88411416]
[0.62302545 4.1695207 0.03759658 4.52663785]
[3.98141545 0.42315403 4.50532033 0.6320994 ]
[3.94646646 0.51572431 4.50602853 0. ]
[3.52561081 0.09799663 4.0668868 0.54322586]
[3.63808518 0.02817457 4.17719886 0.49010053]
[3.31878573 0.33995348 3.86843718 0.65883883]]
>########################################最小值
[0.03759658 0.37445254 0.22807088 0.14881965 0.03759658 0.42315403
0. 0.09799663 0.02817457 0.33995348]
>########################################第5次测试
[[4.47645828 0.59247961 4.01857252 0.03759658 0.6813596 ]
[4.10786393 0.56167882 3.65295386 0.718618 0. ]
[3.89079346 0.04503476 3.4330059 0.60378679 0.60192589]
[3.87831098 0.04503476 3.42029705 0.6240233 0.5222142 ]
[4.51293451 0.63379983 4.05527956 0.03759658 0.75590989]
[0.3160497 3.90055608 0.56420538 4.50532033 4.16373073]
[0.3160497 3.89370655 0.5486597 4.50602853 4.0758083 ]
[0.42812517 3.45689634 0.04433331 4.0668868 3.68779776]
[0.32279564 3.56775134 0.15700388 4.17719886 3.80257994]
[0.63887511 3.25686275 0.19915675 3.86843718 3.4697303 ]]
>########################################最小值
[0.03759658 0. 0.04503476 0.04503476 0.03759658 0.3160497
0.3160497 0.04433331 0.15700388 0.19915675]
[1.9577410235796318, 0.3203584185721923, 0.22674517967844238, 0.17158149471342393, 0.11978560249643681]五、算法效果衡量标准
5.1、轮廓系数
轮廓系数法(Silhouette Coefficient)结合了聚类的凝聚度(Cohesion)和分离度
(Separation),用于评估聚类的效果。该值处于-1~1之间,值越大,表示聚类效果
越好。

5.2、最近簇
最近簇的定义: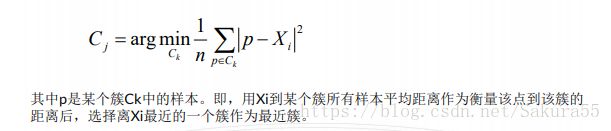
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范
围为[-1,1],且簇内样本的距离越近,簇间样本距离越远,平均轮廓系数越大,聚类效果
越好。
5.3、轮廓系数法代码如下
import numpy as np
from sklearn.cluster import KMeans
from sklearn import metrics
import matplotlib.pyplot as plt
#分割出6个子图,并在1号作图
plt.figure(figsize=(8, 10))
plt.subplot(3, 2, 1)
#初始化原始数字点
x1 = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2) #组合(2,10)
# print(X)
#在1号子图做出原始数据点阵的分布
plt.xlim([0, 10]) #确定
plt.ylim([0, 10])
plt.title('Sample')
plt.scatter(x1, x2)
#点的颜色
colors = ['b','g','r','c','m','y','k','b']
#点的标号
markers = ['o','s','D','v','^','p','*','+']
#簇的个数
tests = [2, 3, 4, 5, 8]
subplot_counter = 1#训练模型
for t in tests:
subplot_counter+= 1
plt.subplot(3, 2, subplot_counter) #从第3个画板开始
kmeans_model = KMeans(n_clusters=t).fit(X)
for i, l in enumerate(kmeans_model.labels_):
plt.plot(x1[i], x2[i], color=colors[l], marker=markers[l],ls='None') #每个画板画点
plt.xlim([0, 10])
plt.ylim([0, 10])
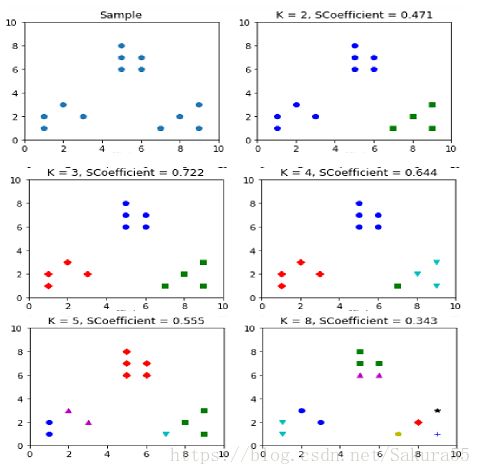
plt.title('K = %s, SCoefficient = %.03f' % (t, metrics.silhouette_score(X,#SCoefficient保留3位小数
kmeans_model.labels_,metric='euclidean')))
#轮廓系数
plt.show()5.4、Canopy算法配合初始聚类
1、聚类最耗费计算的地方是计算对象相似性的时候,Canopy聚类在第一阶段选择简单、计算代价较低的方法计算对象相似性,将相似的对象放在一个子集中,这个子集被叫做Canopy ,通过一系列计算得到若干Canopy,Canopy之间可以是重叠的,但不会存在某个对象不属于任何Canopy的情况,可以把这一阶段看做数据预处理;
2 . 在各个Canopy 内使用传统的聚类方法(如K-means),不属于同一Canopy 的对象
之间不进行相似性计算。(即,根据Canopy算法产生的Canopies代替初始的K个聚类中心点,由于已经将所有数据点进行Canopies有覆盖划分,在计算数据离哪个k- center最近时,不必计算其到所有k-centers的距离,只计算和它在同一个Canopy下的k-centers这样可以提高效率。
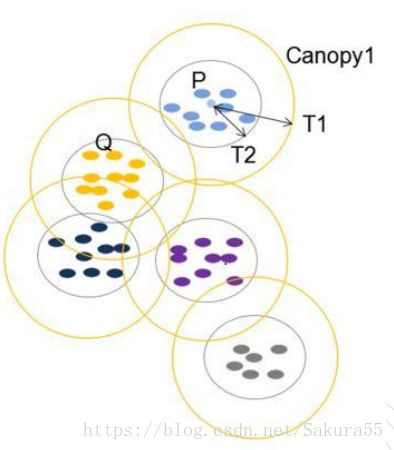
1,首先选择两个距离阈值:T1和T2,其中T1 > T2
2,从list中任取一点P,用低计算成本方法快速计算点P与所有Canopy之间的距(如果当前不存在Canopy,则把点P作为一个Canopy),如果点P与某个Canopy距离在T1以内,则将点P加入到这个Canopy
3,如果点P曾经与某个Canopy的距离在T2以内,则需要把点P从list中删除,这一步是认为点P此时与这个Canopy已经够近了,因此它不可以再做其它Canopy的中心了;
4,重复步骤2、3,直到list为空结束。
5.5、优点
1、Kmeans对噪声抗干扰较弱,通过Canopy对比,将较小的NumPoint的
Cluster直接去掉有利于抗干扰。
2、Canopy选择出来的每个Canopy的centerPoint作为K会更精确。
3、只是针对每个Canopy的内做Kmeans聚类,减少相似计算的数量。
5.6、Calinski-Harabasz Index
六、算法优化
6.1、K-means++
假设已经选取了n个初始聚类中心(在0到K内),则在选取第n+1个聚类中心时:距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心。在选取第一个聚类中心(n=1)时同样通过随机的方法。可以说这也符合我们的直觉:聚类中心当然是互相离得越远越好。
6.2、映射到高维(Kernel k-means)
kernel k-means实际上公式上,就是将每个样本进行一个投射到高维空间的处理,然后再将处理后的数据使用普通的k-means算法思想进行聚类。
6.3、二分法(二分K-means)
首先将所有点作为一个簇,然后将该簇一分为二。之后选择能最大限度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇。以此进行下去,直到簇的数目等于用户给定的数目k为止。
6.4、Mini Batch K-Means
(分批处理)
该算法的迭代步骤有两步:
1:从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心
2:更新质心,适用大数据类型
6.5、迭代自组织数据分析算法(ISODATA)
类别数目随着聚类过程而变化;
对类别数的“合并”:(当聚类结果某一类中样本数太少,或两个类间的距离太近时)
“分裂”(当聚类结果中某一类的类内方差太大,将该类进行分裂)
以下两种方法是拓展
6.6、MCMC采样
MCMC的采样方法,k−MC2就是为了降低 k-means 算法的时间复杂度的改进算法。
使用MCMC采样来近似 D2−sampling 这个过程 在选取候选种子节点时,随机选取一个seeding,然后用MCMC的方法采样出长为M的马尔科夫链,使得马尔科夫链的平稳分布为 p(x) ,从而马尔科夫链达到平稳状态后的那些状态就可以看作是以p(x) 进行采样的样本点。
k-MC^2 算法有一个缺点:
即由于在MCMC过程中,算法使用的提案分布 q(x) 为均匀分布,这导致了潜在的缺点,就是那些样本数较小的聚类中可能不会被选中为候选节点。
6.7、AFK-MC^2
AFK-MC^2关键之处:
在于它使用马尔科夫链对k-Means++进行近似处理,也就是将数据点看做状态点。第一个状态是随机采样的数据点,通过一个随机过程来决定链的状态是否要转移到其他的随机数据点。
状态是否转移与所有点的初始距离是相互独立的(马尔科夫链的稳定状态与初始状态无关), 并且初始距离作为预处理的一部分只计算一次。与k-Means++不同的是,AFK-MC2算法只需要遍历一次数据集。
迭代自组织数据分析算法(ISODATA)的代码演示:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
# X为样本特征,Y为样本簇类别, 共1000个样本,每个样本4个特征,共4个簇,
#簇中心在[-1,-1], [0,0],[1,1], [2,2], 簇方差分别为[0.4, 0.2, 0.2]
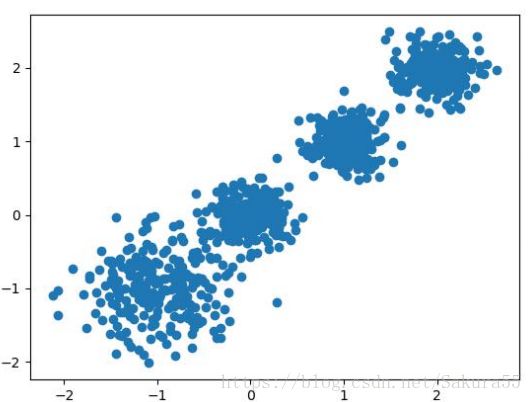
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state =9)
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
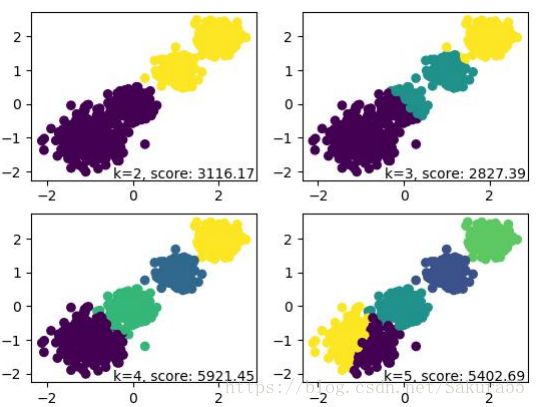
for index, k in enumerate((2,3,4,5)):
plt.subplot(2,2,index+1)
y_pred = MiniBatchKMeans(n_clusters=k, batch_size = 200,random_state=9).fit_predict(X)
score= metrics.calinski_harabaz_score(X, y_pred)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.text(.99, .01, ('k=%d, score: %.2f' % (k,score)),
transform=plt.gca().transAxes, size=10,
horizontalalignment='right')
'''
make_blobs函数是为聚类产生数据集
产生一个数据集和相应的标签
n_samples:表示数据样本点个数,默认值100
n_features:表示数据的维度,默认值是2
centers:产生数据的中心点,默认值3
cluster_std:数据集的标准差,浮点数或者浮点数序列,默认值1.0
center_box:中心确定之后的数据边界,默认值(-10.0, 10.0)
shuffle :洗乱,默认值是True
random_state:官网解释是随机生成器的种子
'''
plt.show()七、Sklearn实现
在sklearn中处理kmeans聚类问题,用到的是 sklearn.cluster.KMeans 这个类
八、案例(图像压缩)
# print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances_argmin
from sklearn.datasets import load_sample_image
from sklearn.utils import shuffle
from time import time
n_colors = 64
# 加载本地数据库里面的图片
china = load_sample_image("china.jpg")
# 转换为浮点数而不是默认的8位整数编码。
# 每一行有255个颜色分类
# 在[0-1]范围内
china = np.array(china, dtype=np.float64) / 255
# 45/5000加载图像并转换为2D numpy数组。
w, h, d = original_shape = tuple(china.shape)
assert d== 3
image_array = np.reshape(china, (w * h, d))
print("Fitting model on a small sub-sample of the data")
t0 = time()
image_array_sample = shuffle(image_array, random_state=0)[:1000]
kmeans = KMeans(n_clusters=n_colors, random_state=0).fit(image_array_sample)
print("done in %0.3fs." % (time() - t0))
# 获取所有的标签
print("Predicting color indices on the full image (k-means)")
t0 = time()
labels = kmeans.predict(image_array)
print("done in %0.3fs." % (time() - t0))
def recreate_image(codebook, labels, w, h):
#重新创建代码簿和标签中的(压缩)图像
d = codebook.shape[1]
image = np.zeros((w, h, d))
label_idx = 0
for i in range(w):
for j in range(h):
image[i][j] = codebook[labels[label_idx]]
label_idx += 1
return image
# 显示所有结果以及原始图像
plt.figure(1)
plt.clf()
ax = plt.axes([0, 0, 1, 1])
plt.axis('off')
plt.title('Original image (96,615 colors)')
plt.imshow(china)
plt.figure(2)
plt.clf()
ax = plt.axes([0, 0, 1, 1])
plt.axis('off')
plt.title('Quantized image (64 colors, K-Means)')
plt.imshow(recreate_image(kmeans.cluster_centers_, labels, w, h))
plt.show()九、代码链接
点击这里