机器学习——分类算法之感知机
机器学习——分类算法之感知机
-
- 前言
- 符号函数
- 感知机模型
- 感知机算法
-
- 1、原始形式
- 2、对偶形式
- 代码
前言
感知机算法（perceptron）是用于二分类的线性分类模型，将输入实例划分为正例和负例的一个超平面，属于判别模型。感知机算法旨在求出将训练数据进行线性划分的分类超平面，基于误分类的损失函数，利用梯度下降法对损失函数进行极小化。
符号函数
符号函数应该都知道，这里简单过一下。
表达式：
f ( x ) = { + 1 x > 0 0 x = 0 − 1 x < 0 (1) f(x)=\left\{\begin{matrix} +1 &x>0 \\ 0&x=0 \\ -1 & x<0 \end{matrix}\right.\tag{1} f(x)=⎩⎨⎧+10−1x>0x=0x<0(1)
图像如下：
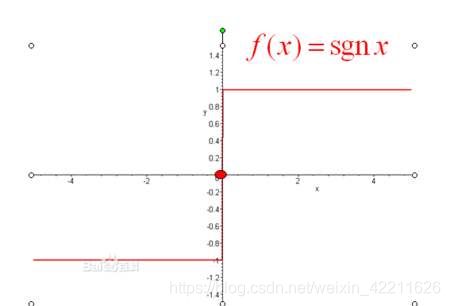
可以看到，符号函数就是一个典型的二分类算法，将输入实例划分正负两类。
感知机模型
定义感知机模型：
假设输入实例 X = { x 1 , x 2 , . . . , x n } X=\{x_{1},x_{2},...,x_{n}\} X={ x1,x2,...,xn}，对应的输出分类 Y = { y 1 , y 2 , . . . , y n } Y=\{y_{1},y_{2},...,y_{n}\} Y={ y1,y2,...,yn}，由输入到输出的感知机模型如下：
f ( x i ) = s i g n ( w ⋅ x i + b ) (2) f(x_{i})=sign(w\cdot x_{i}+b)\tag{2} f(xi)=sign(w⋅xi+b)(2)
其中，w和b为感知机模型参数， w ∈ R N w\in R^{N} w∈RN叫做权值， b ∈ R b\in R b∈R叫做偏置， w ⋅ x w\cdot x w⋅x表示w和x的内积。
下面解释下这个模型：
观察式(2)，感知机模型的假设空间是线性分类模型，即函数集合 { f ∣ f ( x ) = w ⋅ x i + b } \{f|f(x)=w\cdot x_{i} + b\} { f∣f(x)=w⋅xi+b}。
为了方便说明，这里假设 x i = { x i 1 , x i 2 } x_{i}=\{x^{1}_{i},x^{2}_{i}\} xi={ xi1,xi2}即每个样本只有两维特征，那么此时方程 w ⋅ x i + b = 0 w\cdot x_{i}+b =0 w⋅xi+b=0对应于二位空间中的一个超平面，其中w是超平面的法向量，b是超平面的截距。这个超平面将特征空间划分为两个部分，一部分为正类，一部分为负类。此时模型图形如下：
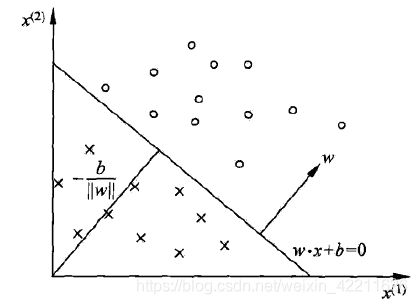
所以，感知机算法就是不断更新学习参数 w w w和 b b b，使得所有样本被正确分类。
感知机算法
1、原始形式
给定一个线性可分的数据集：
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } , y i ∈ { − 1 , + 1 } T=\{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})\},y_{i}\in \{-1,+1\} T={ (x1,y1),(x2,y2),...,(xN,yN)},yi∈{ −1,+1}
感知机算法的目标是求得一个能够将训练集正实例和负实例点完全正确分开的分离超平面，为了找出这样的超平面，即确定感知机的参数 w w w和 b b b，需要定义损失函数，并将损失函数极小化。
怎么选择损失函数？这里选择了误分类点到超平面S的总距离。
输入数据集中的任意一点 x 0 x_{0} x0到超平面的距离：
1 ∣ ∣ w ∣ ∣ 2 ∣ w ⋅ x 0 + b ∣ (3) \frac{1}{||w||_{2}}|w\cdot x_{0}+b|\tag{3} ∣∣w∣∣21∣w⋅x0+b∣(3)
对于误分类点 ( x i , y i ) (x_{i},y{i}) (xi,yi)：
{ w ⋅ x i + b > 0 时 ， y i = − 1 w ⋅ x i + b < 0 时 ， y i = + 1 (4) \left\{\begin{matrix} w\cdot x_{i}+b>0时， &y_{i}=-1 \\ w\cdot x_{i}+b<0时，& y_{i}=+1 \end{matrix}\right.\tag{4} { w⋅xi+b>0时，w⋅xi+b<0时，yi=−1yi=+1(4)
所以式（4）结合起来，就是：
− y i ( w ⋅ x i + b ) > 0 (5) -y_{i}(w\cdot x_{i}+b)>0\tag{5} −yi(w⋅xi+b)>0(5)
因此，误分类点 x i x_{i} xi到超平面S的距离为：
− 1 ∣ ∣ w ∣ ∣ 2 y i ( w ⋅ x i + b ) (6) -\frac{1}{||w||_{2}}y_{i}(w\cdot x_{i}+b)\tag{6} −∣∣w∣∣21yi(w⋅xi+b)(6)
假设超平面的误分类点集合为M，那么所有误分类点大超平面S的总距离为:
− 1 ∣ ∣ w ∣ ∣ 2 ∑ x i ∈ M y i ( w ⋅ x i + b ) (7) -\frac{1}{||w||_{2}}\sum_{x_{i}\in M}y_{i}(w\cdot x_{i}+b)\tag{7} −∣∣w∣∣21xi∈M∑yi(w⋅xi+b)(7)
将感知机的损失函数(也是感知机的经验风险函数)定义如下：
L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) (8) L(w,b)=-\sum_{x_{i}\in M}y_{i}(w \cdot x_{i}+b)\tag{8} L(w,b)=−xi∈M∑yi(w⋅xi+b)(8)
结合式(5)，显然损失函数 L ( w , b ) L(w,b) L(w,b)是非负的。如果没有误分类点，损失函数值为0。而误分类点越少，误分类点离超平面越近，损失函数值就越小。
感知机算法的学习 策略就是取损失函数(8)最小的模型参数 w w w和 b b b。
下面就开始计算梯度：
损失函数极小化，即：
m i n w , b L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) (9) \underset{w,b}{min}L(w,b)=-\sum_{x_{i}\in M}y_{i}(w\cdot x_{i}+b)\tag{9} w,bminL(w,b)=−xi∈M∑yi(w⋅xi+b)(9)
分别对 w w w和 b b b求导
∂ ∂ w L ( w , b ) = − ∑ x i ∈ M y i x i (10) \frac{\partial }{\partial w}L(w,b)=-\sum_{x_{i}\in M}y_{i}x_{i}\tag{10} ∂w∂L(w,b)=−xi∈M∑yixi(10)
∂ ∂ b L ( w , b ) = − ∑ x i ∈ M y i (10) \frac{\partial }{\partial b}L(w,b)=-\sum_{x_{i}\in M}y_{i}\tag{10} ∂b∂L(w,b)=−xi∈M∑yi(10)
参数更新，随机选取一个误分类点(x_{i},y_{i})，对 w , b w,b w,b进行更新：
w ← w + η y i x i (11) w \leftarrow w + \eta y_{i}x_{i}\tag{11} w←w+ηyixi(11)
b ← b + η y i (12) b \leftarrow b + \eta y_{i}\tag{12} b←b+ηyi(12)
η \eta η为学习率，通俗地说用它来设置超平面的移动的幅度，通常取0~1。通过迭代可以是损失函数 L ( w , b ) L(w,b) L(w,b)不断减小，直到为0。
算法的直观解释：
当一个实例点被误分类，即位于分离超平面的错误一侧，则调整 w w w和 b b b的值，使分离超平面向该误分类点的一侧移动，以减少该误分类点与超平面间的距离，直至超平面越过该误差分类点使其被正确分类。
算法流程（直接截图了）：
算法的收敛性这里就不给出证明了，他一定是收敛的，但前提是其数据集是线性可分的。当训练集线性不可分时，感知机算法不收敛，迭代结果会发生震荡。
2、对偶形式
先说明为什么会有对偶形式，或者说相比于原始形式，对偶形式有什么优点？、
再观察式(11)和(12)，对于每一个误分类点，每次都要更新向量：w和b，然后对每一个新的w和b，要判断下一个点是否被误分类，还需要计算一个内积（式(5)）,这样计算量就比较大。
那么再看看对偶形式的感知机。
对偶形式的算法判断一个点是否被误分类，使用如下公式：
y i ( ∑ j = 1 N a j y j x j ⋅ x i + b ) ≤ 0 (13) y_{i}(\sum_{j=1}^{N}a_{j}y_{j}x_{j}\cdot x_{i}+b)\leq 0\tag{13} yi(j=1∑Najyjxj⋅xi+b)≤0(13)
观察上式，虽然说也存在内积计算，但是每次计算的内积是相同的运算，也就是说可以在算法之前，将该内积矩阵提前计算出来，而不必像原始形式必须每次都要计算内积。
代码
import numpy as np
import matplotlib.pylab as plt
#主函数
def main():
#构造训练集
X_train = np.array([[3,3],[4,3],[1,1]])
y = np.array([1,1,-1])
#构造感知机
perceptron = MyPerceptron()
perceptron.fit(X_tain,y)
class MyPerceptron:
def __init__(self):
self.w = None
self.b = 0
self.learning_rate = 1
def fit(self,X_train,y):
self.w = np.zeros(X_train.sape[1])
i = 0
while i < X_train.shape[0]:
X = X_train[i]
y = y[i]
if y * (np.dot(self.w,X)+self.b)<=0:
self.w = self.w +self.learning_rate * np.dot(y,X)
self.b = self.b + self.learning_rate *y
i = 0 #如果是误判点，则从头检测
else:
i += 1