matplotlib如何绘制两点间连线_BD第6课：数据可视化Matplotlib

作为一个数据科学家，或者企业的数据分析师，经过了日夜奋战，终于从浩如烟海的数据中提炼出了有价值的信息，这些信息可能是一堆 CSV 文件，里面有大量的数据，或是一些 Excel 表格，或者保存到 MySQL 数据库中的上百万条记录。OK，不管这些有用的信息是什么格式的，分析完数据，总是要给别人看的，如果直接将这些数据呈现给你的领导或用户，估计他们一定会抓狂，心理一定会说，这难道是“最强大脑”的测试题吗？

其实作为数据的呈现形式，最好使用图表的样式，因为人类的大脑对图形比对文字更有好感。例如，为一个生产胸罩的厂商提供不同尺寸（75 A、80 B等）胸罩全年的销售比例的数据，饼图要远比一堆百分比要好得多。

为了将数据变成所有人都喜欢的图形，就需要使用本文要介绍的数据可视化库 Matplotlib，当然，还有很多类似的程序库，但 Matplotlib 的功能更强大，而且可以很容易与 NumPy、Pandas 等程序库结合在一起使用，Matplotlib 与 NumPy 和 Pandas，并称为 Python 数据分析的三剑客。因此，要想学习如何用 Python 语言进行数据分析，以及深度学习等高度技术，这三个程序库必须学好。

Matplotlib 开发环境搭建

如果读者使用的是 Anaconda Python 开发环境，那么 Matplotlib 已经被集成进 Anaconda，并不需要单独安装，如果读者使用的是标准的 Python 开发环境，可以使用下面的命令安装 Matplotlib。

pip install matplotlib

如果读者要了解 Matplotlib 更详细的情况，请访问官方网站。

安装完 Matplotlib 后，可以测试一下 Matplotlib 是否安装成功。读者可以进入 Python 的 REPL 环境，然后使用下面的语句导入 matplotlib.pyplot 模块，如果不出错，就说明 Matplotlib 已经安装成功了。

import matplotlib.pyplot

基础知识

本文会介绍如何使用 Matplotlib 绘制常见的图形，这些图形包括随机点、柱状图、直方图、盒状图和饼图。

（1）第一个 Matplotlib 程序

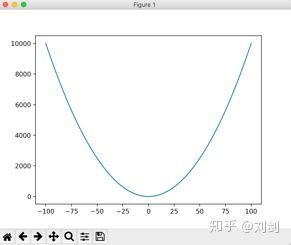
在这一节会用 Matplotlib 来绘制一个一元二次方程曲线，也就是 y = x^2 的图形，学过初等数学的读者应该一下子就会在大脑中出现这个方程的图形。不过这次我们直接用 Matplotlib 在二维坐标系中绘制出来。

在计算机通过程序绘图有两种方式：位图和矢量图，位图就是用一个一个像素点绘制的图形，而矢量图是将多个点进行连接的图形。Matplotlib 所采用的矢量图的绘制方式，也就是连接相邻的两个点形成一条曲线，如果要让曲线平滑，就要让两个点之间的距离尽可能短，也就是说，需要用更多的点来绘制图形，因此，绘制一元二次方程的曲线使用了 200 个点进行绘制。

Matplotlib 有很多函数用于绘制各种图形，其中 plot() 函数用于曲线，需要将 200 个点的 X 坐标和 Y 坐标分别以序列的形式传入 plot() 函数，然后调用 show() 函数显示绘制的图形。

下面的代码使用 plot() 函数绘制一条一元二次方程的曲线，并使用 savefig() 函数将这条曲线保存到 result1.jpg 文件中。

import matplotlib.pyplot as plt
# 生成200个点的X坐标
X = range(-100,101)
# 生成200个点的Y坐标
Y = [x ** 2 for x in X]
# 绘制一元二次曲线
plt.plot(X,Y)
# 将一元二次曲线保存为result1.jpg
plt.savefig('result1.jpg')
# 显示绘制的曲线
plt.show()

运行程序，会看到如图1所示的一元二次曲线。

（2）绘制正弦曲线和余弦曲线

我们会利用 NumPy 和 Matplotlib 绘制正弦曲线和余弦曲线。可能有的读者会问，用 Matplotlib 绘制曲线，怎么把 NumPy 也牵扯进来了，其实 Python 语言内建的 math 模块就有计算正弦（sin）和余弦（cos）的函数，但绘制曲线需要多个坐标点，如果要使用 math 模块中的 sin() 函数和 cos() 函数，还需要计算多个坐标点的值，需要将这些值组成列表，太麻烦，而 NumPy 中的 sin() 函数和 cos() 函数天生就是用来计算多个坐标点的，所以正好和 Matplotlib 搭配。

使用 plot() 函数绘制任何曲线的第一步都是生成若干个坐标点（X,Y），理论上坐标点是越多越好，本节的例子取 100 个坐标点，要计算正弦和余弦，需要的是弧度值，这里只取 0 到 2π 之间的值。所以要将 0 到 2π 分成 100 份，这就形成了 100 个 X 坐标值，然后将这 100 个 X 坐标值一起传入 NumPy 的 sin() 函数或 cos() 函数，就会得到 100 个 Y 坐标轴，最后就可以使用 plot() 函数绘制正弦曲线和余弦曲线了。

下面的代码使用 plot() 函数绘制正弦曲线和余弦曲线。

import math
import matplotlib.pyplot as plt
import numpy
# 将0到2π分成100份，以NumPy数组形式返回这100个X值
X = numpy.linspace(0, 2 * numpy.pi, 100)
# 计算正弦函数每一个X坐标对应的Y坐标，以NumPy数组形式返回这100个Y值
Y = numpy.sin(X)
# 开始绘制正弦曲线
plt.plot(X,Y)
# 显示正弦曲线
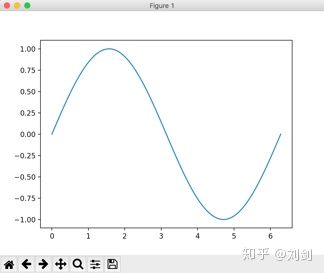
plt.show()

运行程序，会看到如图2所示的正弦曲线。

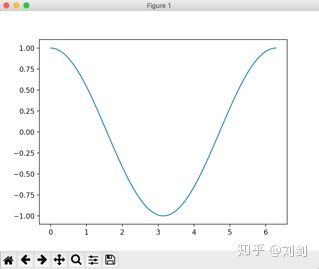
如果将 sin() 函数改成 cos() 函数，会得到如图3所示的余弦曲线。

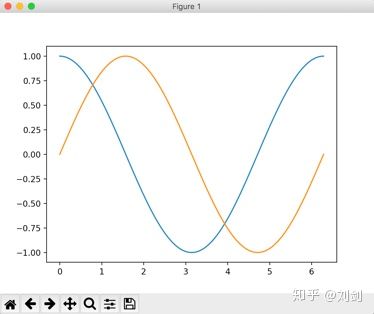
如果调用两次 plot()函数，分别绘制 sin 和 cos 曲线，那么会在同一个二维坐标系显示两条曲线，如图4所示。

（3）绘制随机点

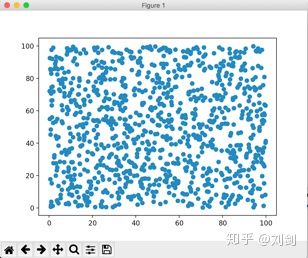
下面的代码使用 scatter() 函数绘制了 1024 个随机点。

import random
import matplotlib.pyplot as plt
count = 1024
# 随机参数1024个随机点的X坐标值
X = [random.random() * 100 for i in range(count)]
# 随机参数1024个随机点的Y坐标值
Y = [random.random() * 100 for i in range(count)] 
# 绘制1024个随机点
plt.scatter(X,Y)
# 显示绘制的随机点
plt.show()

运行程序，会看到如图5所示的随机点。

4）绘制柱状图

使用 bar() 函数可以绘制柱状图。柱状图需要水平的 X 坐标值，以及每一个 X 坐标值对应的 Y 坐标值，从而形成柱状的图，柱状图主要用来纵向对比和横向对比的。例如，根据年份对销售收据进行纵向对比，X 坐标值就表示年份，Y 坐标值表示销售数据。

下面代码使用 bar() 函数绘制了柱状图，并设置了柱的宽度。

import matplotlib.pyplot as plt
# 绘制柱状图，[1980,1985,1990,1995]表示X坐标序列
# [1000,3000,4000,5000]表示Y坐标序列，width表示柱的宽度
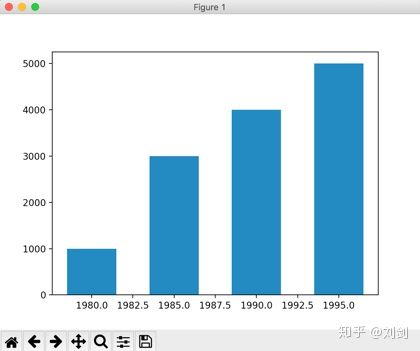
plt.bar([1980,1985,1990,1995],[1000,3000,4000,5000],width = 3)
# 显示状态图
plt.show()

运行程序，会看到如图6所示的柱状图。

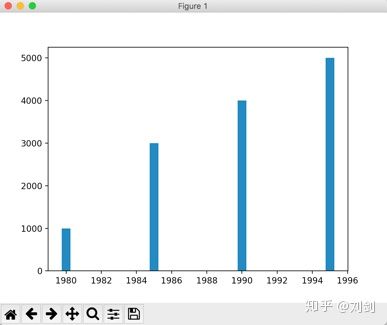
要注意的是，bar() 函数的 width 关键字参数指定的柱的宽度并不是像素宽度。bar() 函数会根据二维坐标系的尺寸，以及 X 坐标值的多少，自动确定每一个柱的宽度。而 width 关键字参数指定的宽度就是这个标准的柱宽度的倍数，该参数值可以是浮点数，如 0.5，表示柱的宽度是标准宽度的 0.5倍，如图7所示。

（5）绘制直方图与盒状图

直方图与柱状图的风格类似，都是由若干个柱组成的，但直方图和柱状图的含义却有很大差异。直方图是用来观察分布状态的，而柱状图是用来看每一个 X 坐标值的 Y 值的。也就是说，直方图关注的是分布，并不关心具体的某个值，而柱状图关心的是具体某个值。

盒状图与直方图尽管形态上有很大差异，但含义类似，都是用于表示分布状态的，不过盒状图还有一个功能，就是能体现数据的平均值。

使用 hist() 函数可以绘制直方图，该函数需要传入两个参数值，第 1 个参数值用于指定数据序列，第 2 个参数值表示 X 轴的分布区域，一般这个参数值与数据序列的个数相同。boxplot() 函数用于绘制盒状图，该函数只需要传入数据序列即可。

下面的代码使用 randn() 函数生成了 100 个正态分布的随机数，并使用 hist() 函数与 boxplot() 函数绘制这 100 个随机数的分布状态。

import numpy as np
import matplotlib.pyplot as plt
# 产生100个正态分布的随机数
data = np.random.randn(100)
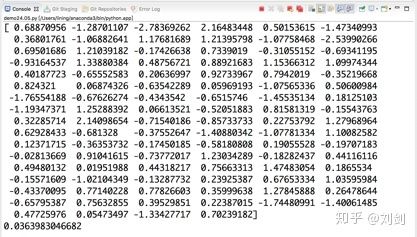
print(data)
# 计算100个随机数的平均数
print(np.average(data))
# 在同一个窗口创建两个二维坐标系，左侧的坐标系显示直方图，右侧的坐标系显示盒状图
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(8,8))
# 绘制直方图
ax1.hist(data,100)
# 绘制盒状图
ax2.boxplot(data)
# 显示直方图和盒状图
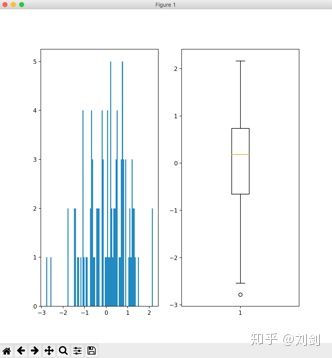
plt.show()

运行程序，会在窗口中显示如图8所示的直方图和盒状图。

运行程序后，会在 Console 中输入如图9所示的 100 个随机数和平均值。

图9 100 个正态分布随机数和平均值

我们可以看到，这 100 个正态分布的随机数的平均值是 0.0363983046682，而盒装图中间的红线表示了平均值，盒装图的纵坐标表示 100 个随机数的取值范围，从目前来看，随机数大多都在 -2 到 2 之间。盒装图中间的红线正好在 0 的位置靠上一点，也就是大概 0.0363983046682 的位置。

不管是盒状图，还是直方图，都可以了解这 100 个随机数的分布，先来看盒状图，中间的方块就表示数据主要集中的区域，从这个区域可以估算，这 100 个随机数主要集中在 -1.5 到 1.5 之间（大概估算）。在直方图中，X 轴表示数据的分布范围，越密集的地方，数据越多。很明显，在 -1 和 1 之间是最密的，所以数据主要会集中在这个区域。

要注意的是，直方图和盒状图是用来看数据分布的，这个分布只是一个覆盖率问题，并不能用非常精确的值表示，只是一个趋势而已。

（6）绘制饼图

使用 pie() 函数可以绘制饼图，饼图一般是用来呈现比例的，如特斯拉电动车中中国、美国、日本等国家的销售量占全球销售量的比例。pie() 函数的使用方法比较简单，只需要传入比例数据序即可。

下面的代码使用 pie() 函数绘制了 5 个数值的饼图。

import matplotlib.pyplot as plt
data = [5,67,23,43,64]
# 绘制饼图
plt.pie(data)
# 显示饼图
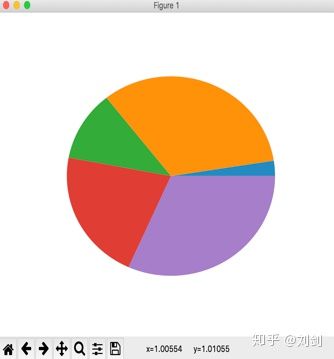
plt.show()

运行程序后，会在窗口中显示如图10所示的饼图。

如果你有疑问欢迎加微信咨询：

也可以关注我的公众号想我提问：