将一维数据(序列)转化为二维数据(图像)的方法汇总GAFS, MTF, Recurrence plot,STFT
将一维序列数据转化为二维图像数据的方法汇总 详细 全面
- 一、背景
- 二、方法介绍
-
- 格拉米角场 GAFs
-
- 原理
- 实现步骤
- 调用示例
- 马尔可夫变迁场 MTF
-
- 原理
- 实现步骤
- 调用示例
- 递归图 Recurrence Plot
-
- 原理
- 调用示例
- 短时傅里叶变换 STFT
- 原理
- 实现步骤
- 调用示例
- References
- 总结
一、背景
虽然深度学习方法(1D CNN, RNN, LSTM 等)可以直接处理一维数据,但是当前的深度学习方法主要还是处理二维结构数据的,特别是在计算机视觉CV以及自然语言处理NLP领域,各种各样的方法层出不穷。因此,如果能够将一维序列数据转化为二维(图像)数据, 则可以直接结合CV以及NLP领域的方法,是不是很有趣!
二、方法介绍
格拉米角场 GAFs
原理
将缩放后的1D序列数据从直角坐标系统转换到极坐标系统,然后通过考虑不同点之间的角度和/差以识别不同时间点的时间相关性。取决于是做角度和还是角度差,有两种实现方法:GASF(对应做角度和), GADF(对应做角度差)。
实现步骤
Step 1:缩放,将数据范围缩放到[-1,1]或者[0, 1], 公式如下:
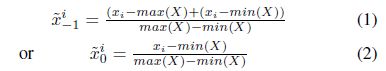
Step 2: 将缩放后的序列数据转换到极坐标系统,即将数值看作夹角余弦值,时间戳看作半径,公式如下:
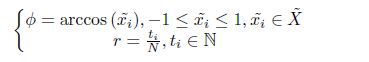
注: 若数据缩放范围为[-1, 1],则转换后的角度范围为[0, π \pi π];若缩放范围为[0, 1],则转换后的角度范围为[0, π \pi π/2]。
Step 3:
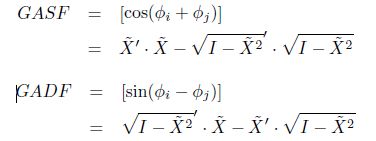
可以看到,最终GASF和GADF的计算转化到直角坐标系下变成了“类似”内积的操作。
效率问题:对于长度为n的序列数据,转换后的GAFs尺寸为[n, n]的矩阵,可以采用PAA(分段聚合近似)先将序列长度减小,然后在转换。 所谓的PAA就是:将序列分段,然后通过平均将每个段内的子序列压缩为一个数值, 简单吧!
调用示例
Python工具包pytl中已经提供了API,另外,笔者自行实现代码, 想要查看实现细节以及获取更多测试用例,可从我的 链接获取。
'''
EnvironmentPython 3.6, pyts: 0.11.0, Pandas: 1.0.3
'''
from mpl_toolkits.axes_grid1 import make_axes_locatable
from pyts.datasets import load_gunpoint
from pyts.image import GramianAngularField
# call API
X, _, _, _ = load_gunpoint(return_X_y=True)
gasf = GramianAngularField(method='summation')
X_gasf = gasf.transform(X)
gadf = GramianAngularField(method='difference')
X_gadf = gadf.transform(X)
plt.figure()
plt.suptitle('gunpoint_index_' + str(0))
ax1 = plt.subplot(121)
ax1.plot(np.arange(len(rescale(X[k][:]))), rescale(X[k][:]))
plt.title('rescaled time series')
ax2 = plt.subplot(122, polar=True)
r = np.array(range(1, len(X[k]) + 1)) / 150
theta = np.arccos(np.array(rescale(X[k][:]))) * 2 * np.pi # radian -> Angle
ax2.plot(theta, r, color='r', linewidth=3)
plt.title('polar system')
plt.show()
plt.figure()
plt.suptitle('gunpoint_index_' + str(0))
ax1 = plt.subplot(121)
plt.imshow(X_gasf[k])
plt.title('GASF')
divider = make_axes_locatable(ax1)
cax = divider.append_axes("right", size="5%", pad=0.2) # Create an axes at the given *position*=right with the same height (or width) of the main axes
plt.colorbar(cax=cax)
ax2 = plt.subplot(122)
plt.imshow(X_gadf[k])
plt.title('GASF')
divider = make_axes_locatable(ax2)
cax = divider.append_axes("right", size="5%",
pad=0.2) # Create an axes at the given *position*=right with the same height (or width) of the main axes
plt.colorbar(cax=cax)
plt.show()
结果如下图所示:
缩放后的序列数据以及在极坐标系统的表示:
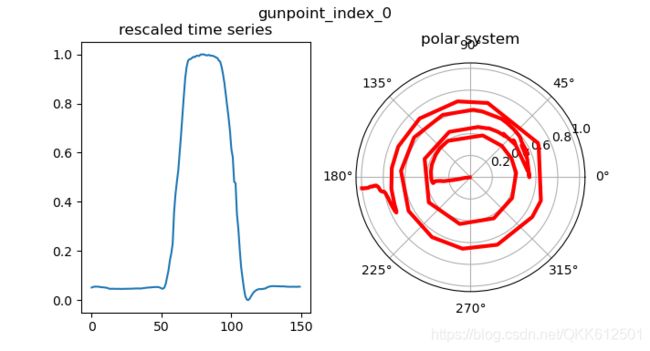
转换后的GASF和GADF:
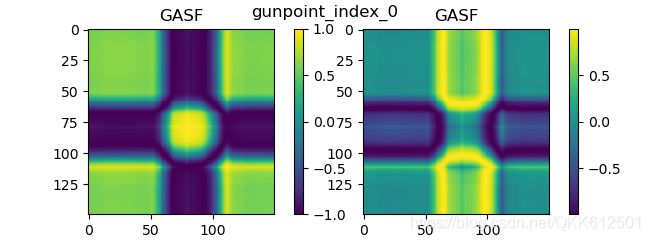
马尔可夫变迁场 MTF
原理
基于1阶马尔可夫链,由于马尔科夫转移矩阵对序列的时间依赖并不敏感,因此作者考虑了时间位置关系提出了所谓的MTF。
实现步骤
Step 1: 首先将序列数据(长度为n)按照其取值范围划分为Q个bins (类似于分位数), 每个数据点 i 属于一个唯一的qi ( ∈ \in ∈ {1,2, …, Q}).
Step 2: 构建马尔科夫转移矩阵W,矩阵尺寸为:[Q, Q], 其中W[i,j]由qi中的数据被qj中的数据紧邻的频率决定,其计算公式如下:
w i , j = ∑ ∀ x ∈ q i , y ∈ q j , x + 1 = y 1 / ∑ j = 1 Q w i , j w_{i,j}=\sum_{\forall x \in q_{i}, y \in q_{j},x+1=y}1/\sum_{j=1}^{Q}w_{i,j} wi,j=∑∀x∈qi,y∈qj,x+1=y1/∑j=1Qwi,j
Step 3:构建马尔科夫变迁场M, 矩阵尺寸为:[n, n], M[i,j]的值为W[qi, qj]
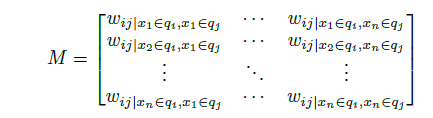
效率问题:原因与GAFs类似,为了提高效率,设法减小M的尺寸,思路与PAA类似,将M网格化,然后每个网格中的子图用其平均值替代。
调用示例
Python工具包pytl中已经提供了API,另外,笔者自行实现代码, 想要查看实现细节以及获取更多测试用例,可从我的 github 链接获取。
'''
EnvironmentPython 3.6, pyts: 0.11.0, Pandas: 1.0.3
'''
from mpl_toolkits.axes_grid1 import make_axes_locatable
from pyts.datasets import load_gunpoint
from pyts.image import MarkovTransitionField
## call API
X, _, _, _ = load_gunpoint(return_X_y=True)
mtf = MarkovTransitionField()
fullimage = mtf.transform(X)
# downscale MTF of the time series (without paa) through mean operation
batch = int(len(X[0]) / s)
patch = []
for p in range(s):
for q in range(s):
patch.append(np.mean(fullimage[0][p * batch:(p + 1) * batch, q * batch:(q + 1) * batch]))
# reshape
patchimage = np.array(patch).reshape(s, s)
plt.figure()
plt.suptitle('gunpoint_index_' + str(k))
ax1 = plt.subplot(121)
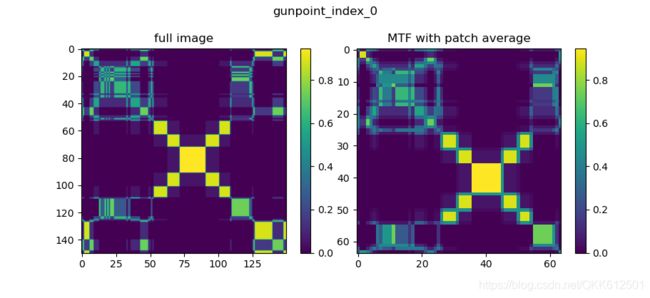
plt.imshow(fullimage[k])
plt.title('full image')
divider = make_axes_locatable(ax1)
cax = divider.append_axes("right", size="5%", pad=0.2)
plt.colorbar(cax=cax)
ax2 = plt.subplot(122)
plt.imshow(patchimage)
plt.title('MTF with patch average')
divider = make_axes_locatable(ax2)
cax = divider.append_axes("right", size="5%", pad=0.2)
plt.colorbar(cax=cax)
plt.show()
递归图 Recurrence Plot
递归图(recurrence plot,RP)是分析时间序列周期性、混沌性以及非平稳性的一个重要方法,用它可以揭示时间序列的内部结构,给出有关相似性、信息量和预测性的先验知识,递归图特别适合短时间序列数据,可以检验时间序列的平稳性、内在相似性。
原理
递归图是表示从原始时间序列提取的轨迹之间的距离的图像
给定时间序列数据: ( x 1 , … , x n ) (x_1, \ldots, x_n) (x1,…,xn),提取到的轨迹为:
x ⃗ i = ( x i , x i + τ , … , x i + ( m − 1 ) τ ) , ∀ i ∈ { 1 , … , n − ( m − 1 ) τ } \vec{x}_i = (x_i, x_{i + \tau}, \ldots, x_{i + (m - 1)\tau}), \quad \forall i \in \{1, \ldots, n - (m - 1)\tau \} xi=(xi,xi+τ,…,xi+(m−1)τ),∀i∈{ 1,…,n−(m−1)τ}
其中: m m m是轨迹的维数, τ \tau τ是时延。 递归图R是轨迹之间的成对距离,计算如下:
R i , j = Θ ( ε − ∥ x ⃗ i − x ⃗ j ∥ ) , ∀ i , j ∈ { 1 , … , n − ( m − 1 ) τ } R_{i, j} = \Theta(\varepsilon - \| \vec{x}_i - \vec{x}_j \|), \quad \forall i,j \in \{1, \ldots, n - (m - 1)\tau \} Ri,j=Θ(ε−∥xi−xj∥),∀i,j∈{ 1,…,n−(m−1)τ}
其中, Θ \Theta Θ为Heaviside函数,而 ε \varepsilon ε 是阈值。
调用示例
'''
EnvironmentPython 3.6, pyts: 0.11.0, Pandas: 1.0.3
'''
from mpl_toolkits.axes_grid1 import make_axes_locatable
from pyts.datasets import load_gunpoint
from pyts.image import RecurrencePlot
X, _, _, _ = load_gunpoint(return_X_y=True)
rp = RecurrencePlot(dimension=3, time_delay=3)
X_new = rp.transform(X)
rp2 = RecurrencePlot(dimension=3, time_delay=10)
X_new2 = rp2.transform(X)
plt.figure()
plt.suptitle('gunpoint_index_0')
ax1 = plt.subplot(121)
plt.imshow(X_new[0])
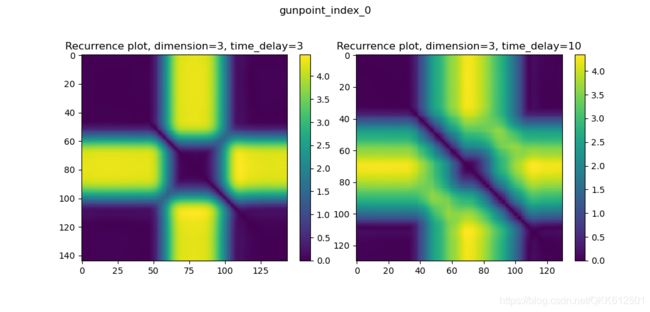
plt.title('Recurrence plot, dimension=3, time_delay=3')
divider = make_axes_locatable(ax1)
cax = divider.append_axes("right", size="5%", pad=0.2)
plt.colorbar(cax=cax)
ax1 = plt.subplot(122)
plt.imshow(X_new2[0])
plt.title('Recurrence plot, dimension=3, time_delay=10')
divider = make_axes_locatable(ax1)
cax = divider.append_axes("right", size="5%", pad=0.2)
plt.colorbar(cax=cax)
plt.show()
短时傅里叶变换 STFT
STFT可看作一种量化非平稳信号的频率和相位含量随时间变化的方式。.
原理
通过添加窗函数(窗函数的长度是固定的),首先对时域信号加窗,通过滑动窗口的方式将原始时域信号分割为多个片段,然后对每一个片段进行FFT变换,从而得到信号的时频谱(保留了时域信息)。
实现步骤
假设序列的长度为 T T T, τ \tau τ为窗口窗口长度, s s s为滑动步长,W表示窗函数, 则STFT可以计算为:
S T F T ( τ , s ) ( X ) [ m , k ] = ∑ t = 1 T X [ t ] ⋅ W ( t − s m ) ⋅ e x p { − j 2 π k / τ ⋅ ( t − s m ) } STFT^{(\tau,s)}(X)_{[m,k]}=\sum_{t=1}^{T}X_{[t]} \cdot W(t-sm)\cdot exp\{-j2\pi k /\tau \cdot (t-sm)\} STFT(τ,s)(X)[m,k]=∑t=1TX[t]⋅W(t−sm)⋅exp{ −j2πk/τ⋅(t−sm)}
变换后的STFT尺寸为:[M, K], M代表时间维度,K代表频率幅值(复数形式),为方便起见,假设 s = τ s=\tau s=τ, 即窗口之间没有重叠,则
M = T / τ M=T/\tau M=T/τ,
K = ⌊ τ ⌋ K =\lfloor \tau \rfloor K=⌊τ⌋/2 + 1
注:相比于DFT, STFT在某种程度上帮助我们恢复时间分辨率,然而在可达到的时间分辨率和频率之间会发生权衡,这就是所谓的不确定性原理。具体来说,窗口的宽度( τ \tau τ)越大,频域分辨率就越高,相应地,时域分辨率越低;窗口的宽度( τ \tau τ)越小,频域分辨率就越低,相应地,时域分辨率越高。
调用示例
python包 scipy提供STFT的API,具体官方文档介绍见:https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.stft.html
scipy.signal.stft(x,fs = 1.0,window =‘hann’,nperseg = 256,noverlap = None,nfft = None,detrend = False,return_oneside = True,boundary
=‘zeros’,padded = True,axis = -1 )
参数解释:
x: 时域信号;
fs: 信号的采样频率;
window: 窗函数;
nperseg: 窗函数长度;
noverlap: 相邻窗口的重叠长度,默认为50%;
nfft: FFT的长度,默认为nperseg。如大于nperseg会自动进行零填充;
return_oneside : True返回复数实部,None返回复数。
示例代码:
"""
@author: masterqkk, [email protected]
Environment:
python: 3.6
Pandas: 1.0.3
matplotlib: 3.2.1
"""
import pickle
import numpy as np
import matplotlib.pyplot as plt
import scipy.signal as scisig
from mpl_toolkits.axes_grid1 import make_axes_locatable
from pyts.datasets import load_gunpoint
if __name__ == '__main__':
X, _, _, _ = load_gunpoint(return_X_y=True)
fs = 10e3 # sampling frequency
N = 1e5 # 10 s 1signal
amp = 2 * np.sqrt(2)
time = np.arange(N) / float(fs)
mod = 500 * np.cos(2 * np.pi * 0.25 * time)
carrier = amp * np.sin(2 * np.pi * 3e3 * time + mod)
noise_power = 0.01 * fs / 2
noise = np.random.normal(loc=0.0, scale=np.sqrt(noise_power), size=time.shape)
noise *= np.exp(-time / 5)
x = carrier + noise # signal with noise
per_seg_length = 1000 # window length
f, t, Zxx = scisig.stft(x, fs, nperseg=per_seg_length, noverlap=0, nfft=per_seg_length, padded=False)
print('Zxx.shaope: {}'.format(Zxx.shape))
plt.figure()
plt.suptitle('gunpoint_index_0')
ax1 = plt.subplot(211)
ax1.plot(x)
plt.title('signal with noise')
ax2 = plt.subplot(212)
ax2.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp)
plt.title('STFT Magnitude')
ax2.set_ylabel('Frequency [Hz]')
ax2.set_xlabel('Time [sec]')
plt.show()
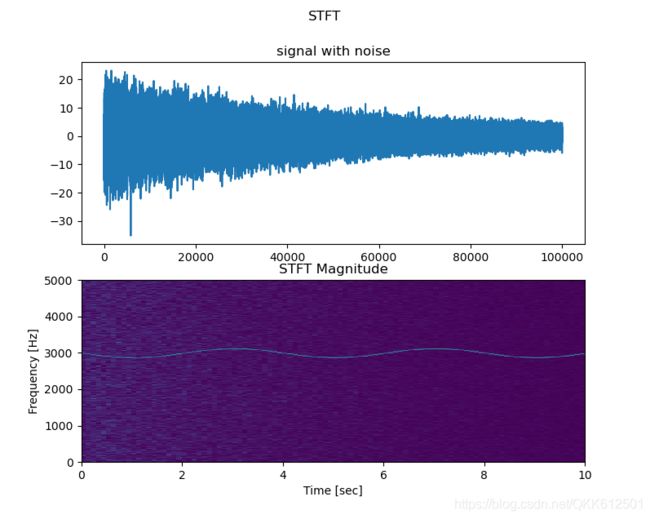
运行结果:
得到STFT结果尺寸为:
Zxx.shaope: (501, 101), 频率成分的数量为 ⌊ 1000 ⌋ \lfloor 1000 \rfloor ⌊1000⌋/2 + 1 = 501, 窗口片段的长度为1e5/1000 + 1=101 (此处应该是进行了pad)
References
1.Imaging Time-Series to Improve Classification and Imputation
2.Encoding Time Series as Images for Visual Inspection and Classification Using Tiled Convolutional Neural Networks
3.J.-P Eckmann, S. Oliffson Kamphorst and D Ruelle, “Recurrence Plots of Dynamical Systems”. Europhysics Letters (1987)
4.Stoica, Petre, and Randolph Moses,Spectral Analysis of Signals, Prentice Hall, 2005
总结
希望能帮助到大家, 未完待续。欢迎交流:[email protected]