Python数据挖掘部分相关扩展库学习
python数据挖掘部分相关扩展库学习
参考学习资料:《Python数据分析与挖掘实战》
1 NumPy
提供数组支持以及相应的高效处理函数
import numpy as np
a = np.array([2, 0, 1, 5])
print(a)
print(a[:3]) # 引用前三个数字(切片)
print(a.min())
a.sort() # 此操作直接修改a
b = np.array([[1, 2, 3], [4, 5, 6]]) # 创建二维数组
print(b * b) # 输出数组的平方阵
[2 0 1 5]
[2 0 1]
0
[[ 1 4 9]
[16 25 36]]
2 SciPy
提供矩阵支持以及矩阵相关的数值计算模块
# 求解非线性方程组
from scipy.optimize import fsolve
def f(x):
x1 = x[0]
x2 = x[1]
return [2*x1 - x2**2 -1, x1**2 -x2 -2]
result = fsolve(f, [1, 1])
print(result)
[1.91963957 1.68501606]
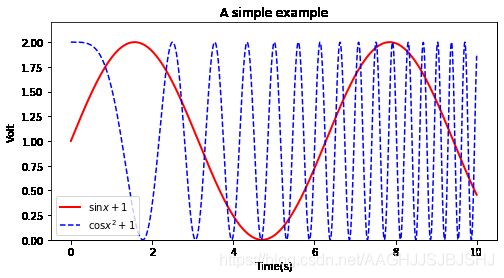
3 Matplotlib
强大的数据可视化工具、作图库
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0, 10, 1000)
y = np.sin(x) + 1
z = np.cos(x**2) + 1
plt.figure(figsize = (8,4))
plt.plot(x, y, label = '$\sin x+1$',color = 'red', linewidth = 2)
plt.plot(x, z, 'b--', label = '$\cos x^2+1$')
plt.xlabel('Time(s)')
plt.ylabel('Volt')
plt.title('A simple example')
plt.ylim(0, 2.2)
plt.legend()
plt.show()
4 pandas
强大、灵活的数据分析和探索工具
pandas基本的数据结构是Series和DataFrame
import numpy as np
import pandas as pd
s = pd.Series([1, 2, 3], index = ['a', 'b', 'c'])
d = pd.DataFrame([[1, 2, 3], [4, 5, 6]], columns = ['a', 'b', 'c'])
d1 = pd.DataFrame(s)
d.head() # 预览前5行数据,这里全部查看
d.describe() # 数据基本统计量
| a | b | c | |
|---|---|---|---|
| count | 2.00000 | 2.00000 | 2.00000 |
| mean | 2.50000 | 3.50000 | 4.50000 |
| std | 2.12132 | 2.12132 | 2.12132 |
| min | 1.00000 | 2.00000 | 3.00000 |
| 25% | 1.75000 | 2.75000 | 3.75000 |
| 50% | 2.50000 | 3.50000 | 4.50000 |
| 75% | 3.25000 | 4.25000 | 5.25000 |
| max | 4.00000 | 5.00000 | 6.00000 |
5 StatsModels
统计建模和计量经济学,包括描述统计、统计模型估计和推断
from statsmodels.tsa.stattools import adfuller as ADF # 导入ADF检验
import numpy as np
ADF(np.random.rand(100))
(-11.185166734080935,
2.4452619254700322e-20,
0,
99,
{'1%': -3.498198082189098,
'5%': -2.891208211860468,
'10%': -2.5825959973472097},
15.7792788675915)
6 scikit-learn
支持回归、分类、聚类等强大的机器学习库
from sklearn.linear_model import LinearRegression# 导入线性回归模型
model = LinearRegression() # 建立线性回归模型
print(model)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
# 监督模型
model.predict(X_new) # 预测新样本
model.predict_proba(X_new) # 预测概率,仅对某些模型有用(LR)
model.score() # 得分越高,fit越好
# 非监督模型
model.transform() # 从数据中学到新的“基空间”
model.fit_transform() # 从数据中新学到新的基并将这个数据按照这组“基”进行转化
from sklearn import datasets
iris = datasets.load_iris()
print(iris.data.shape) # 查看数据集大小
from sklearn import svm
clf = svm.LinearSVC() # 建立线性SVM分类器
clf.fit(iris.data, iris.target) # 用数据训练模型
clf.predict([[5.0, 3.6, 1.3, 0.25]]) # 训练好模型后,输入新的数据进行预测
clf.coef_ # 查看训练好模型的参数
(150, 4)
array([[ 0.18424151, 0.45122686, -0.80794634, -0.45071563],
[ 0.05697002, -0.90045931, 0.40728976, -0.9594009 ],
[-0.8505339 , -0.98660947, 1.38113399, 1.86551995]])
clf.score(iris.data, iris.target)
0.9666666666666667
7 Keras
深度学习库,用于建立神经网络以及深度学习模型
需要搭建环境
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD
model = Sequential() # 模型初始化
model.add(Dense(20, 64)) # 添加输入层(20节点)、第一隐藏层(64节点)的连接
model.add(Activation('tanh')) # 第一隐藏层用tanh作为激活函数
model.add(Dropout(0.5)) # 使用Dropout防止过拟合
model.add(Dense(64, 64)) # 添加第一隐藏层(64节点)、第二隐藏层(64节点)
model.add(Activation('tanh')) # 第二隐藏层用tanh作为激活函数
model.add(Dropout(0.5)) # 使用Dropout防止过拟合
model.add(Dense(64, 1)) # 添加第二隐藏层(64节点)、输出层(1节点)的连接
model.add(Activation('sigmoid')) # 输出层用sigmoid作为激活函数
sgd = SGD(lr=0.1, decay=1e-6, momentum=0.9, nestrov=True) # 定义求解算法
model.complie(loss='mean_squared_error', optimizer=sgd) # 编译生成模型,损失函数为平均误差平方和
model.fit(X_train, y_train, nb_epoch=20, batch_size=16) # 训练模型
score = model.evaluate(X_test, y_test, batch_size=16) # 测试模型
8 Gensim
用来做文本主题模型的库,可用于文本挖掘
import gensim, logging
logging.basicConfig(format='%(asctime)s :%(levelname)s :%(message)s', level = logging.INFO) # logging用于输出训练日志
sentence = [['first', 'sentence'], ['second', 'sentence']]
model = gensim.models.Word2Vec(sentence, min_count=1)
print(model['sentence']) # 输出单词sentence的词向量
[-4.3921093e-03 -4.1555655e-03 -4.6353755e-03 -9.0758421e-04
1.0104279e-03 4.7344534e-04 4.9750379e-04 -1.9801888e-03
3.9610104e-03 4.5447927e-03 2.3985980e-03 -4.9385368e-03
-4.2100544e-03 -3.6711162e-03 -4.6847081e-03 -4.2208371e-04
1.5523760e-03 -1.2773386e-03 1.5698618e-03 2.3681845e-04
4.1909250e-03 -1.1569046e-04 -6.1990012e-04 1.6961809e-03
-3.0097782e-03 -2.2817680e-03 -3.5721802e-03 -9.6812792e-04
4.9223113e-03 -2.5558346e-03 -3.4400518e-03 4.1700946e-03
1.5960374e-03 3.7051921e-03 -1.2132508e-03 -3.6483407e-03
-1.7364629e-04 2.5401772e-03 2.6047304e-03 -3.6287934e-03
-2.7433275e-03 4.1096192e-03 1.7566864e-03 -3.4833241e-03
3.1620823e-03 -2.2903190e-04 -1.1041900e-03 3.9621242e-03
-8.6754531e-04 -4.9830682e-04 4.3459381e-03 -4.7724689e-03
4.2731795e-03 1.6964840e-03 -2.6452250e-03 -1.8090474e-03
-1.5309388e-03 -2.2350897e-03 -2.3615484e-03 -4.2477851e-03
-4.2006909e-03 4.6970434e-03 4.9966001e-03 2.0446957e-03
-4.3111700e-03 9.3228521e-04 -7.8243780e-04 3.2738579e-05
-3.6026731e-03 3.0883260e-03 -4.1066012e-03 -9.0799549e-06
-1.2111863e-03 -1.4822575e-05 -9.9706114e-04 -2.7378965e-03
-4.0914682e-03 1.0044479e-03 -1.8251943e-03 -3.2508206e-03
1.1792558e-03 3.0473061e-03 -1.9985032e-03 4.9585253e-03
-2.0646052e-03 1.5070011e-03 1.3249324e-03 4.4992031e-03
-3.8824442e-03 3.5415601e-03 1.5354829e-03 1.2283857e-04
3.0506381e-03 -1.8657360e-03 -1.8609000e-03 3.4154786e-03
-2.7230517e-03 -3.8653433e-03 3.9593326e-03 1.1934722e-03]