寒假CS每日打卡 Feb.21st

---

算法部分

1.Acwing 入门组每日一题
题目：跳一跳
近来，跳一跳这款小游戏风靡全国，受到不少玩家的喜爱。

简化后的跳一跳规则如下：玩家每次从当前方块跳到下一个方块，如果没有跳到下一个方块上则游戏结束。

如果跳到了方块上，但没有跳到方块的中心则获得 1 分；跳到方块中心时，若上一次的得分为 1 分或这是本局游戏的第一次跳跃则此次得分为 2 分，否则此次得分比上一次得分多两分（即连续跳到方块中心时，总得分将 +2，+4，+6，+8…）。

现在给出一个人跳一跳的全过程，请你求出他本局游戏的得分（按照题目描述的规则）。

输入格式
输入包含多个数字，用空格分隔，每个数字都是 1，2，0 之一，1 表示此次跳跃跳到了方块上但是没有跳到中心，2 表示此次跳跃跳到了方块上并且跳到了方块中心，0 表示此次跳跃没有跳到方块上（此时游戏结束）。

输出格式
输出一个整数，为本局游戏的得分（在本题的规则下）。

数据范围
对于所有评测用例，输入的数字不超过 30 个，保证 0 正好出现一次且为最后一个数字。

输入样例：
1 1 2 2 2 1 1 2 2 0
输出样例：
22

代码：

#include 

using namespace std;

int main(){
     
    int ans = 0, pre = 0, a;
    
    while(cin >> a && a){
     
        if(a == 1)
            ans += 1, pre = 0;
        else
            pre += 2, ans += pre;
    }
    cout << ans;
    return 0;
}

2.LeetCode 每日一题
题目：绝对差不超过限制的最长连续子数组
给你一个整数数组 nums ，和一个表示限制的整数 limit，请你返回最长连续子数组的长度，该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。

如果不存在满足条件的子数组，则返回 0 。

示例 1：
输入：nums = [8,2,4,7], limit = 4
输出：2
解释：所有子数组如下：
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4.
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4.
因此，满足题意的最长子数组的长度为 2 。

示例 2：
输入：nums = [10,1,2,4,7,2], limit = 5
输出：4
解释：满足题意的最长子数组是 [2,4,7,2]，其最大绝对差 |2-7| = 5 <= 5 。

示例 3：
输入：nums = [4,2,2,2,4,4,2,2], limit = 0
输出：3

提示：
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
0 <= limit <= 10^9

题解：
  双指针，右指针每次移动一，左指针移动到相应位置使得区间满足条件，条件满足单调性，可以使用单调队列来优化。

代码：

class Solution {
     
public:
    int longestSubarray(vector<int>& nums, int limit) {
     
        int ans = 0, le = 0, ri = 0;
        //分别存储最小队列、最大队列
        deque<int> a, b;

        while(ri < nums.size()){
     
        //维护单调队列
            while(!a.empty() && nums[a.back()] > nums[ri])
                a.pop_back();
            a.push_back(ri);
            while(!b.empty() && nums[b.back()] < nums[ri])
                b.pop_back();
            b.push_back(ri);
            //移动左指针使得区间满足条件
            while(!a.empty() && !b.empty() && nums[b.front()] - nums[a.front()] > limit){
     
                if(le == a.front())
                    a.pop_front();
                if(le == b.front())
                    b.pop_front();
                ++ le;
            }
            ans = max(ans, ri - le + 1);
            //右指针每次移动1
            ++ ri;
        }
        return ans;
    }
};

3.地图中的最高点
题目：
给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。

如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
如果 isWater[i][j] == 1 ，格子 (i, j) 是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度：

每个格子的高度都必须是非负的。
如果一个格子是是 水域 ，那么它的高度必须为 0 。
任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）
找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：

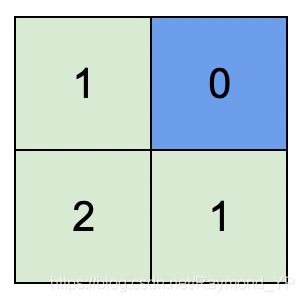
输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。

示例 2：

输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。

提示：
m == isWater.length
n == isWater[i].length
1 <= m, n <= 1000
isWater[i][j] 要么是 0 ，要么是 1 。
至少有 1 个水域格子。

题解：
  多源点BFS，每次扩展一格高度就会增加1 。

代码：

//记录二维坐标
typedef pair<int, int> PII;

class Solution {
     
public:
    vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
     
        int n = isWater.size(), m = isWater[0].size();
        int fx[4][2] = {
     {
     0, 1}, {
     0, -1}, {
     1, 0}, {
     -1, 0}};
        vector<vector<int>> ans(n, vector<int>(m, -1));
        queue<PII> Q;

        for(int i = 0; i < n; i ++)
            for(int j = 0; j < m; j ++)
            	//记录bfs起点
                if(isWater[i][j]){
     
                    Q.push(PII(i, j));
                    ans[i][j] = 0;
                }

        while(!Q.empty()){
     
            PII cur = Q.front();
            Q.pop();
            //向4个方向扩展
            for(int i = 0; i < 4; i ++){
     
                int r = cur.first + fx[i][0];
                int c = cur.second + fx[i][1];
                //未越界 并且 之前没有走到过
                if(r >= 0 && r < n && c >= 0 && c < m && ans[r][c] == -1){
     
                    ans[r][c] = ans[cur.first][cur.second] + 1;
                    Q.push(PII(r, c));
                }
            }
        }
        return ans;
    }
};

4.最长的美好子字符串
题目：
当一个字符串 s 包含的每一种字母的大写和小写形式 同时 出现在 s 中，就称这个字符串 s 是 美好 字符串。比方说，“abABB” 是美好字符串，因为 ‘A’ 和 ‘a’ 同时出现了，且 ‘B’ 和 ‘b’ 也同时出现了。然而，“abA” 不是美好字符串因为 ‘b’ 出现了，而 ‘B’ 没有出现。

给你一个字符串 s ，请你返回 s 最长的 美好子字符串 。如果有多个答案，请你返回 最早 出现的一个。如果不存在美好子字符串，请你返回一个空字符串。

示例 1：
输入：s = “YazaAay”
输出：“aAa”
解释：“aAa” 是一个美好字符串，因为这个子串中仅含一种字母，其小写形式 ‘a’ 和大写形式 ‘A’ 也同时出现了。
“aAa” 是最长的美好子字符串。

示例 2：
输入：s = “Bb”
输出：“Bb”
解释：“Bb” 是美好字符串，因为 ‘B’ 和 ‘b’ 都出现了。整个字符串也是原字符串的子字符串。

示例 3：
输入：s = “c”
输出：""
解释：没有美好子字符串。

示例 4：
输入：s = “dDzeE”
输出：“dD”
解释：“dD” 和 “eE” 都是最长美好子字符串。
由于有多个美好子字符串，返回 “dD” ，因为它出现得最早。

提示：
1 <= s.length <= 100
s 只包含大写和小写英文字母。

题解：
  暴力枚举，复杂度为O(n³)。

代码：

class Solution {
     
public:
    string longestNiceSubstring(string s) {
     
        int len = 0;
        string ans;
		//枚举区间端点
        for(int i = 0; i < s.length(); i ++){
     
            for(int j = i + 1; j < s.length(); j ++){
     
                bool op = true;
                //使用集合判断字符是否出现
                unordered_set<char> set;
                for(int k = i; k <= j; k ++)
                    set.insert(s[k]);
                for(char c : set)
                    if(set.find(c - 32) == set.end() && set.find(c + 32) == set.end())
                        op = false;
                if(op && len < j - i + 1)
                    len = j - i + 1, ans = s.substr(i, len);
            }
        }
        return ans;
    }
};

5.执行乘法运算的最大分数
题目：
给你两个长度分别 n 和 m 的整数数组 nums 和 multipliers ，其中 n >= m ，数组下标 从 1 开始 计数。

初始时，你的分数为 0 。你需要执行恰好 m 步操作。在第 i 步操作（从 1 开始 计数）中，需要：

选择数组 nums 开头处或者末尾处 的整数 x 。
你获得 multipliers[i] * x 分，并累加到你的分数中。
将 x 从数组 nums 中移除。
在执行 m 步操作后，返回 最大 分数。

示例 1：
输入：nums = [1,2,3], multipliers = [3,2,1]
输出：14
解释：一种最优解决方案如下：

• 选择末尾处的整数 3 ，[1,2,3] ，得 3 * 3 = 9 分，累加到分数中。
• 选择末尾处的整数 2 ，[1,2] ，得 2 * 2 = 4 分，累加到分数中。
• 选择末尾处的整数 1 ，[1] ，得 1 * 1 = 1 分，累加到分数中。
  总分数为 9 + 4 + 1 = 14 。

示例 2：
输入：nums = [-5,-3,-3,-2,7,1], multipliers = [-10,-5,3,4,6]
输出：102
解释：一种最优解决方案如下：

• 选择开头处的整数 -5 ，[-5,-3,-3,-2,7,1] ，得 -5 * -10 = 50 分，累加到分数中。
• 选择开头处的整数 -3 ，[-3,-3,-2,7,1] ，得 -3 * -5 = 15 分，累加到分数中。
• 选择开头处的整数 -3 ，[-3,-2,7,1] ，得 -3 * 3 = -9 分，累加到分数中。
• 选择末尾处的整数 1 ，[-2,7,1] ，得 1 * 4 = 4 分，累加到分数中。
• 选择末尾处的整数 7 ，[-2,7] ，得 7 * 6 = 42 分，累加到分数中。
  总分数为 50 + 15 - 9 + 4 + 42 = 102 。

提示：
n == nums.length
m == multipliers.length
1 <= m <= 103
m <= n <= 105
-1000 <= nums[i], multipliers[i] <= 1000

题解：
  区间dp裸题，需要变换一下，将末尾的字符单独提出出来，还要注意题目给的nums中间部分有些情况下是没有用的。
状态表示：dp[i][j]代表使用前面i个字符，后面j个字符能得到的最优解
状态转移 ：dp[i][j] = max(dp[i][j - 1] + b[j] * multipliers[i + j - 1], dp[i - 1][j] + a[i] * multipliers[i + j - 1]);

代码：

class Solution {
     
public:
    int maximumScore(vector<int>& nums, vector<int>& multipliers) {
     
        int n = nums.size(), m = multipliers.size(), ans = INT_MIN;
        vector<int> a, b;

        a.push_back(0);
        b.push_back(0);
        //a记录开头数字 b记录末尾数字
        for(int i = 0; i < m; i ++)    
            a.push_back(nums[i]);
        for(int j = n - 1; j >= n - m; j --)
            b.push_back(nums[j]);
        
        // 区间dp
        vector<vector<int>> dp(m + 1, vector<int>(m + 1));
        for(int i = 0; i <= m; i ++){
     
            for(int j = 0; j <= m; j ++){
     
                if(i + j > m)
                    break;
                if(i == 0 && j == 0)
                    dp[i][j] = 0;
                else if(i == 0)
                    dp[i][j] = dp[i][j - 1] + b[j] * multipliers[i + j - 1];
                else if(j == 0)
                    dp[i][j] = dp[i - 1][j] + a[i] * multipliers[i + j - 1];
                else
                    dp[i][j] = max(dp[i][j - 1] + b[j] * multipliers[i + j - 1], dp[i - 1][j] + a[i] * multipliers[i + j - 1]);
                //i + j 为当前位置，为m代表正好取了m个数字
                if(i + j == m)
                    ans = max(ans, dp[i][j]);
            }
        }
        return ans;
    }
};