最短路径笔记,记录一下,防止忘记!(2.25 更新,补充更全,绝对能看懂!)
文章目录
- 一、最短路是什么?
-
- 1.Dijkstra(迪杰斯特拉) 算法
- 2.多源最短路
- 二、算法介绍?
- 三、算法演示
- 四、题目示例
-
- 1.模版题(ZCMU-1624)
- 2.实现代码
- 总结
一、最短路是什么?
最短路算法其实有很多种:
1.Dijkstra(迪杰斯特拉) 算法
2.多源最短路
鄙人不才,今天先收录使用临接矩阵和队列实现Dij算法,其他的算法以后再做补充······
2021.2.25 更新笔记(更新具体最短路的注释和图解)
今天有好多同学反应说是最短路代码单看看不懂,确实是这样,当初我学习的时候也看了一晚上一头雾水,今天添加一些便于理解的注释,希望能帮助到大家少走弯路
二、算法介绍?
(狄克斯特拉1930年5月11日生于荷兰鹿特丹的一个知识分子家庭,在兄弟姊妹4人中排行第三。他的父亲是一名化学家和发明家,曾担任荷兰化学会主席。他母亲则是一位数学家。他成功地设计并实现了在有障碍物的两个地点之间找出一条最短路径的高效算法,这个算法被命名为“狄克斯特拉算法”,解决了机器人学中的一个十分关键的问题,即运动路径规划问题,至今仍被广泛应用,被认为是利用“贪心法”(greedy method)设计算法的一个成功范例。)
完整算法的图:
我们这里定义图的编号为:
1 2 3
4 5 6
7 8 9
图1:初始化的图,其中包含边的权值(耗时)。(这里图是有向图)。
图2:确定起点,然后向能直接走到的点走一下,记录此时的估计值:2 6 9.。
图3:找到距离起点最近的点,是正东边的那个点,这时候我们耗费权值为2。然后我们进行松弛操作,从起点到其东南方的点直接到的权值耗费为6,但是我们通过刚刚选定的点,我们找到了到这个点更近的方式,所以这个时候我们说从起点到其东南方向的点的权值更新值从6变成了5。这个时候我们就完成了第一次松弛操作。
图4:依旧是找距离起点最近的点。然后松弛我们发现这个时候从起点到其东南方的点的耗费权值从5又变成了4.这个时候我们完成了第二个松弛。
之后的方式同上:选定距离起点最近的点v。然后通过点v进行松弛操作。我们发现能够通过增加走到目的地方式的复杂度(多转弯)的方式我们能够松弛掉权值,使得耗费的权值更小。
三、算法演示
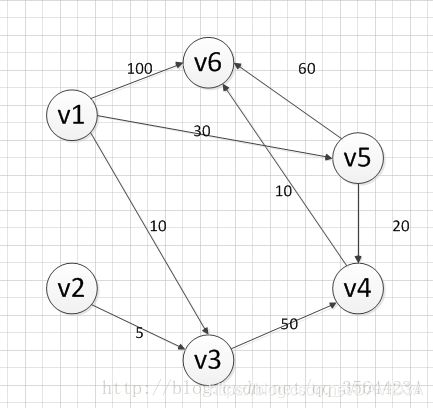
首先第一步,我们先要把所有的数据读到程序里,那么用什么办法来存储路径数据呢?
聪明的你肯定想到了(maybe?),我们可以用临阶矩阵实现,也就是说,建立一个二维的数组。
存数据的时候,比如说这道题,给你的数据会是:
6 8
1 6 100
1 5 30
4 6 10
1 3 10
2 3 5
3 4 50
5 4 20
5 6 60
这里的6表示6个结点,8表示会有8组数据
下面的8组数据前两个是节点,第三个是权值
我们把前两个数据作为map(二维数据)的横纵坐标,第三个数据作为存的值
(这里有有向图和无向图的区别,如果是无向图我们需要双向导通,具体操作看代码)
另外,记得把i==j的数据标为0(本身到本身距离为0)
第二步,我们申明一个dis数组,用来存放从V1到各个顶点距离的数据
(这里注意,题目不一样需求也不一样,可能问的是其他点到某点的距离,这个灵活变通好伐)
显然呢,我们可以根据本题得到dis初始值为[0,INF,10,INF,30,100]
这里有几点可能容易引起困惑,第一个0指的是从1到1的距离,显然是0(本身到本身),你可以把这个看成是一个1*6的矩阵,纵坐标表示的就是1,2,3,4,5,6,这样我们就将能从1直接到某处的距离标记了下来
接下来进行查找的操作,我们要从这个dis里找到最短的路径,显然是从1到3的距离是10,我们把这个距离送到min里,如何flag=3,作为之后vis访问过的依据(vis[flag] = 1)
之后呢,回到我们刚才建立好的图,我们从flag行开始寻找,看一下此时flag行的数据,我们可以知道是[10,5,0,50,0,0],然后列从1到6跑一个循环,判断条件是(map[flag][j]+min
就这样,dis的值不断的变化,最终我们得到的结果就是从v1到任意一点的最短路径,是不是很简单呢?
四、题目示例
1.模版题(ZCMU-1624)
链接: ZCMU-1624.
1624: 最短路
Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 368 Solved: 99
[Submit][Status][Web Board]
Description
有n个城市编号为1—n,m条路,告诉你每条路的长度,求给定两点的最短路径长度。
Input
T 组数据
每组数据第一行有两个正整数n,m(n<=1000,m<=10000)分别表示城市的数量和路的条数,接下来m行,每行3个整数a,b,c,表示城市a和城市b之间有一条c长度的路
最后一行输入两个整数x,y。
Output
输出城市 x 到城市 y 的最短路径。如果不存在输出-1。
Sample Input
2
3 2
1 2 2
2 3 3
1 3
4 2
1 2 3
1 3 2
1 4
Sample Output
5
-1
2.实现代码
代码如下(示例):
#include下面是一个从别人博客转载的利用队列实现的,贴在这里便于以后查看:
void spfa()
{
memset(dis, 0x3f, sizeof dis);
dis[1] = 0; vis[1] = 1;//vis记录是否在队列里
queue q;
q.push(1);
register int u, v;
while(q.size())
{
u = q.front(); q.pop(); vis[u] = 0;
for(int i = head[u]; ~i; i = e[i].nxt)//向外发散
{
v = e[i].to;
if(dis[u] + e[i].w < dis[v])
{
dis[v] = dis[u] + e[i].w;
if(!vis[v]) q.push(v), vis[v] = 1; //不在队列中,那就放进去更新别的点
}
}
}
}
几个需要注意的小点:
1.解题前需要判断这是一个有向图还是一个无向图,在读入数据的时候还是有差距的
2.值得注意的是,可能会出现找不到最短路径的情况,也就是说,某地到某地的路程为无穷(maxn),此时记得输出-1即可
3.这题有几个变化,比如现在模版题是输出x到y的最短路径,有些时候可能只是叫你输出从1到任意城市的最短路径,这点知道一下就可以了
总结
提示:这里对文章进行总结:
最短路Dij算法在ACM竞赛中占重要地位,是一个需要熟记熟练使用的算法,不熟的话多打几次模版题就可以了。