基于阈值的图像二值化方法MATLAB
一、目录
1.以经验值128作为阈值分割
2.手动调试,寻找更好的阈值
3.自动选择合适的阈值方法
二、实验方法
首先选取灰度值128为阈值,使用固定阈值的二值化处理,观察分割效果。得出两组由灰度值小于128和大于等于128 的像素组成的像素群,做出两组像素群的高斯分布,通过观察正态分布曲线和多次手动调试,最终选择合适的阈值为113。另外,为减少了手动调试的次数,本文还采取了观察图像的灰度直方图的方法,从视觉上直观快速地选择合适的阈值。
实验显示固定阈值128不能在图像的任何区域都创建一个无空洞的分割,本文采取了全局阈值Otsu法和全局阈值迭代法来自动分析阈值,得到了较好的分割效果。但实验结果仍存在较少的空洞,最后进行空洞填充,实现二值图像的最佳转化。
三、实验步骤
3.1 固定阈值法
(1)计算均值和方差
手动设置经验阈值128。在MATLAB中导入原始图片,使用rgb2gray()函数将图片转化为灰度图像,方便后续的计算和处理。然后,使用find()函数分别找出图像中灰度值小于和大于128的两组像素。接下来使用mean()函数和std()函数,分别求出两组灰度值数据的均值和标准差,见表4.1。


表4.1 两组灰度值数据的均值和标准差
分组 灰度值均值(EX) 灰度值标准差(Std)
灰度小于128的组 70.23 13.13
灰度大于128的组 157.83 18.85
(2)绘制和分析高斯分布图像
根据表4.1的两组均值和标准差,可以绘制出两组灰度值的正态分布图像,如图4.1所示。
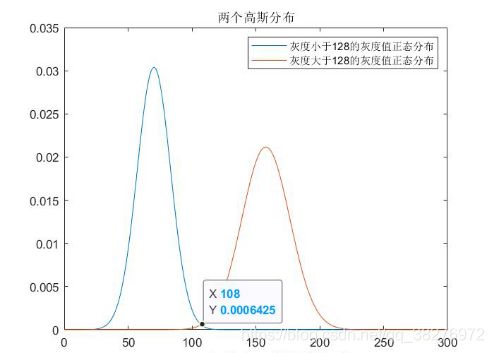
图4.1 以128为阈值的两组灰度值的正态分布图像
在上图中,蓝色曲线代表灰度小于128的灰度值正态分布,橙色曲线代表灰度大于128的灰度值正态分布。通过观察可以看出,高斯分布曲线可以很好的呈现出左右两个独立的波峰,说明阈值128基本可以把物体和背景的灰度值有效地分开。
但是,两个曲线还存在交叉重叠的部分。两条有重叠部分,代表了图像中像素被误分的概率,原为目标物体的被分为背景,或者原为背景被分为目标物体,从而导致图像分割效果不佳。
(3)以128为阈值进行固定阈值分割
使用matlab中DIP工具箱函数im2bw,可以利用阈值变换法把灰度图像转换成二值图像。
BW = im2bw(I,level);其中level就是设置的阈值。level取值范围[0, 1]。输出图像 BW 将输入图像I中亮度值大于 level 的像素替换为值1 (白色),其他替换为值0(黑色)。如果不指定level,im2bw默认为0.5。
设置level为128/256,得到的分割效果图如图4.2所示。硬币的像素点标记成了白色,背景标记成了黑色,算法基本可以把硬币和背景分开,但是在两个硬币中也存在一些黑色区域。这是因为拍摄照片光照的原因,固定的阈值128会施加在整张图片上,但是图片中不同区域之间适合的阈值不一定相同,所以对于某些光照不均的图像,这种阈值分割方法效果就不是很好。

为寻找是否有比128更好的阈值,本文通过多次手动调试阈值,观察高斯分布曲线的情况,最终得出以113为阈值能实现该图像更好的分割。因手动调试阈值麻烦且精确度不高,下面本文采用观察图像灰度直方图的方式来确定最优的固定阈值。
(4)观察灰度直方图选择最优固定阈值
灰度直方图是关于灰度级分布的函数。对图像中不同灰度级别出现的次数进行统计,统计后进行绘制直方图,横坐标表示灰度级别0-255,纵坐标表示每个灰度级别在图像中出现的次数,一般还会对次数进行归一化。灰度图像中画面比较简单且对象物的灰度分布比较有规律时,背景和对象物在图像的灰度直方图上各形成一个波峰,由于每两个波峰间形成一个低谷,因而选择双峰间低谷处所对应的灰度值为阈值,可将两个区域分离。
调用matlab中的imhist(I)函数,绘制出灰度图像的灰度直方图,图像如图4.3所示。观察该灰度直方图,图像中有两个波峰,选择双峰间低谷处所对应的灰度值为113作为最优阈值,可以得到更好的分割效果。以113为阈值的分割效果图和高斯分布图如图4.4,4.5所示。

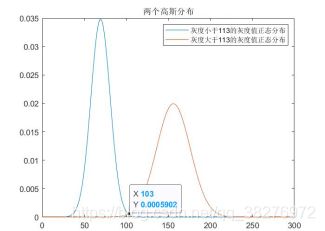
首先,对比113和128两个阈值的分割效果图,以113为阈值的分割效果图中硬币的黑色区域明显减少,从视觉上可以直观地看出分割效果有了明显的进步。然后,对比两个阈值对应的高斯分布图像,可以清晰地看出以113为阈值的高斯分布图像中两个正态曲线交叉重叠部分较少,说明分割效果得到了较大的提升。
因此,通过多次手动调试观察正态分布曲线、观察图像的灰度直方图,得出存在比经验值128分割效果更好的阈值,这个阈值是灰度值113。
4.2自动阈值选择法
为减少人工选取阈值的工作量,提升分割效果,本文选取两种自动阈值选择算法(全局阈值迭代法、全局阈值Otsu法)来自动选取合适的阈值,进行二值化分割。
(1)全局阈值迭代法
迭代法阈值获取的方法:
①选取一个的初始估计值T0(选择平均灰度)。
②使用初始预估值T0分割图像。这样便会生成两组像素集合:G1由所有灰度值大于T0的像素组成,而G2由所有灰度值小于或等于T0的像素组成。
③对G1和G2中所有像素计算平均灰度值u1和u2。
④计算新的阈值:T=1/2(u1+u2)。
重复步骤②到④,直到得到的T-T0的绝对值小于一个事先定义的参数ΔT,迭代结束,将T最为最优阈值进行分割。在本算法中选择T为图像灰度值的平均值;ΔT为0.1,用于控制迭代的次数。
使用while循环编写迭代程序得出最优阈值,使用im2bw函数对图像做二值化处理,最后采用imfill()函数对孔洞进行填充。填充空洞前后的最优阈值为分割效果图如下图4.6所示,


图4.6 全局阈值迭代法分割效果图(填充空洞前、后)
计算结果显示,最优阈值为116,这与我们观察直方图得到的最佳阈值很相近,充分证明了算法的有效性。当物体和背景的灰度直方图间存在一个相当清晰的波谷时,这个简单的算法工作得很好。这种方法的缺点也很明显,它仅能分割双峰明显的图像,对复杂图像并达不到很好的效果。
(2)全局阈值Otsu法
otsu法(最大类间方差法)是一种自适应的阈值确定的方法。使用的是聚类的思想,把图像的灰度数按灰度级分成2个部分,使得两个部分之间的灰度值差异最大,每个部分之间的灰度差异最小,通过方差的计算来寻找一个合适的灰度级别来划分。所以可以在二值化的时候采用otsu算法来自动选取阈值进行二值化。otsu算法被认为是图像分割中阈值选取的最佳算法,计算简单,不受图像亮度和对比度的影响。因此,使类间方差最大的分割意味着错分概率最小。
使用Matlab中的函数graythresh()可以找到图片合适的阈值level,这个阈值在[0, 1]范围内,该阈值可以传递给im2bw完成灰度图像转换为二值图像的操作,最后进行空洞填充。利用这个阈值通常比人为设定的阈值能更好地把一张灰度图像转换为二值图像。填充空洞前后的全局阈值Otsu法的分割效果图如图4.7所示。


图4.7 全局阈值Otsu法的分割效果图(填充空洞前、后)
计算结果显示,全局阈值Otsu法得出的最佳阈值为112.4,和我们观察灰度直方图得出的113非常接近,进一步证明了观察的准确性和算法的可靠性。
5.结论
通过上述实验,可以汇总得出如下结论。
(1)将该图像转化为灰度图像,灰度值大于128的像素群灰度值均值为70.23,标准差为13.13;小于128的像素群灰度值均值为157.83,标准差为18.85。
(2)按两组的均值和标准差绘制的两个高斯分布曲线,能很好地呈现出左右两个波峰,但是中间有部分交叉重叠。两条有重叠部分,代表了图像中像素被误分的概率,原为目标物体的被分为背景,或者原为背景被分为目标物体,从而导致图像分割效果不佳。说明阈值128基本可以实现物体和背景的二值化分割,但仍然有分割效果不好的点。
(3)通过多次手动调试阈值,观察正态曲线的分布情况,得出最优阈值为113。为缩短手动调试的时间,本文绘制出该图像的灰度直方图,通过观察可以帮助直观地发现最优阈值。
(4)实验结果显示阈值128不能在图像的所有区域创建无空洞的分割,在硬币所在位置内也包含和背景一样的灰度。所以本文选择全局阈值迭代法和全局阈值Otsu法,自动分析选取合适的阈值,并使用matlab中的imfill()函数填充空洞,得到最佳分割效果。两种方法的最优阈值分别为和116和112.4,均与手动调试最佳阈值113非常接近。
MATLAB代码实现:
close all;
clc;
clear;
% 1.计算均值、方差
Thre=128; %手动设置阈值
I=imread('photo.jpg'); %载入真彩色图像
I=rgb2gray(I); %转换为灰度图像
figure;imhist(I);
a=find(I<Thre);
b=find(I>=Thre);
e1=mean(I(a));
e2=mean(I(b));
std1 = std(im2double(I(a)) * 255, 0);
std2 = std(im2double(I(b)) * 255, 0);
% 2.绘制两个高斯分布
x=0:1:300;
%y1=gaussmf(x,[std1 e1]);
y1=normpdf(x,e1,std1);
figure,
plot(x,y1)
hold on
%y2=gaussmf(x,[std2 e2]);
y2=normpdf(x,e2,std2);
plot(x,y2)
xlabel('gaussmf, P1=[e1 v1],P2=[e2 v2]')
legend('灰度小于128的灰度值正态分布','灰度大于128的灰度值正态分布')
title('两个高斯分布')
% 3.固定阈值分割方法
I1=im2bw(I,Thre/256);
figure,imshow(I1),title('固定阈值分割方法(取经验值为128)');
% 4.自动阈值选择分割法
f=im2double(I); %数据类型转换
T=0.5*(min(f(:))+max(f(:)));
done=false;
while ~done
g=f>=T;
Tn=0.5*(mean(f(g))+mean(f(~g)));
done = abs(T-Tn)<0.1;
T=Tn;
end
disp('Threshold(T)-Iterative');%显示文字
T
r=im2bw(f,T);
figure;
subplot(221),imshow(r);
xlabel('迭代法分割效果图(填充前)');
r=imfill(r,'holes');%将原图填充孔洞
subplot(222),imshow(r);
xlabel('迭代法分割效果图(填充后)');
Th=graythresh(f);%阈值
disp('Global Thresholding- Otsu''s Method');
Th
s=im2bw(f,Th);
subplot(223),imshow(s);
xlabel('Otsu法分割效果图(填充前)');
s=imfill(s,'holes');%将原图填充du孔洞
subplot(224),imshow(s);
xlabel('Otsu法分割效果图(填充后)');