DougLeaMrConcurrency

LeetCode面试题：100道（下）

目录
.面试题 03 数组中重复的数字
.面试题 04 二维数组中的查找
.面试题 05 替换空格
.面试题 06 从尾到头打印链表
.面试题 07 重建二叉树
.面试题 09 用两个栈实现队列
.面试题 10- I 斐波那契数列
.面试题 10- II 青蛙跳台阶问题
.面试题 11 旋转数组的最小数字
.面试题 12 矩阵中的路径
.面试题 13 机器人的运动范围
.面试题 14- I 剪绳子
.面试题 14- II 剪绳子 II
.面试题 15 二进制中 1 的个数
.面试题 16 数值的整数次方
.面试题 17 打印从 1 到最大的 n 位数
.面试题 18 删除链表的节点
.面试题 19 正则表达式匹配
.面试题 20 表示数值的字符串
.面试题 21 调整数组顺序使奇数位于偶数前面
.面试题 22 链表中倒数第 k 个节点
.面试题 24 反转链表
.面试题 25 合并两个排序的链表
.面试题 26 树的子结构
.面试题 27 二叉树的镜像
.面试题 28 对称的二叉树
.面试题 29 顺时针打印矩阵
.面试题 30 包含 min 函数的栈
.面试题 31 栈的压入、弹出序列
.面试题 32 - I 从上到下打印二叉树
.面试题 32 - II 从上到下打印二叉树 II
.面试题 32 - III 从上到下打印二叉树 III
.面试题 33 二叉搜索树的后序遍历序列
.面试题 34 二叉树中和为某一值的路径
.面试题 35 复杂链表的复制
.面试题 36 二叉搜索树与双向链表
.面试题 37 序列化二叉树
.面试题 38 字符串的排列
.面试题 39 数组中出现次数超过一半的数字
.面试题 40 最小的 k 个数
.面试题 41 数据流中的中位数
.面试题 42 连续子数组的最大和
.面试题 43 1 ～ n 整数中 1 出现的次数
.面试题 44 数字序列中某一位的数字
.面试题 45 把数组排成最小的数
.面试题 46 把数字翻译成字符串
.面试题 47 礼物的最大价值
.面试题 48 最长不含重复字符的子字符串
.面试题 49 丑数
.面试题 50 第一个只出现一次的字符
.面试题 51 数组中的逆序对
.面试题 52 两个链表的第一个公共节点
.面试题 53 - I 在排序数组中查找数字 I
.面试题 53 - II 0 ～ n-1 中缺失的数字
.面试题 54 二叉搜索树的第 k 大节点
.面试题 55 - I 二叉树的深度
.面试题 55 - II 平衡二叉树
.面试题 56 - I 数组中数字出现的次数
.面试题 56 - II 数组中数字出现的次数 II
.面试题 57 和为 s 的两个数字
.面试题 58 - I 翻转单词顺序
.面试题 58 - II 左旋转字符串
.面试题 59 - I 滑动窗口的最大值
.面试题 59 - II 队列的最大值
.面试题 60 n 个骰子的点数
.面试题 61 扑克牌中的顺子
.面试题 62 圆圈中最后剩下的数字
.面试题 63 股票的最大利润
.面试题 64 求 1+2++n
.面试题 65 不用加减乘除做加法
.面试题 66 构建乘积数组
.面试题 67 把字符串转换成整数
.面试题 68 - I 二叉搜索树的最近公共祖先
.面试题 68 - II 二叉树的最近公共祖先

面试题 03. 数组中重复的数字

题目描述

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0 ～ n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3

限制：

2 <= n <= 100000

解法

0 ～ n-1 范围内的数，分别还原到对应的位置上，如：数字 2 交换到下标为 2 的位置。

若交换过程中发现重复，则直接返回。

Python3

class Solution:
    def findRepeatNumber(self, nums: List[int]) -> int:
        for i, num in enumerate(nums):
            while i != num:
                if num == nums[num]:
                    return num
                nums[i], nums[num] = nums[num], nums[i]
                num = nums[i]
        return -1

Java

class Solution {
     
    public int findRepeatNumber(int[] nums) {
     
        for (int i = 0, n = nums.length; i < n; ++i) {
     
            while (nums[i] != i) {
     
                if (nums[i] == nums[nums[i]]) return nums[i];
                swap(nums, i, nums[i]);
            }
        }
        return -1;
    }

    private void swap(int[] nums, int i, int j) {
     
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

Kotlin

class Solution {
     
    fun findRepeatNumber(nums: IntArray): Int {
     
        for (i in nums.indices) {
     
            while (i != nums[i]) {
     
                if (nums[i] == nums[nums[i]]) {
     
                    return nums[i];
                }
                swap(nums, i, nums[i]);
            }
        }
        return -1;
    }

    fun swap(nums: IntArray, i: Int, j: Int) {
     
        var t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @return {number}
 */
var findRepeatNumber = function (nums) {
     
  let m = {
     };
  for (let num of nums) {
     
    if (m[num]) return num;
    m[num] = 1;
  }
};

Go

func findRepeatNumber(nums []int) int {
     
    for i := 0; i < len(nums); i++ {
     
        for nums[i] != i {
     
            if nums[i] == nums[nums[i]] {
     
                return nums[i]
            }
            nums[i], nums[nums[i]] = nums[nums[i]], nums[i]
        }
    }
    return -1
}

C++

class Solution {
     
public:
    int findRepeatNumber(vector<int>& nums) {
     
        int len = nums.size();
        for (int i = 0; i < len; i++) {
     
            while (i != nums[i]) {
     
                // 这一位的值，不等于这一位的数字
                if (nums[i] == nums[nums[i]]) {
     
                    // 如果在交换的过程中，发现了相等的数字，直接返回
                    return nums[i];
                }

                swap(nums[i], nums[nums[i]]);
            }
        }

        return 0;
    }
};

…

面试题 04. 二维数组中的查找

题目描述

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

限制：

0 <= n <= 1000
0 <= m <= 1000

解法

从左下角（或右上角）开始查找即可。

Python3

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix or not matrix[0]:
            return False
        rows, cols = len(matrix), len(matrix[0])
        i, j = rows - 1, 0
        while i >= 0 and j < cols:
            if matrix[i][j] == target:
                return True
            if matrix[i][j] > target:
                i -= 1
            else:
                j += 1
        return False

Java

class Solution {
     
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
     
        int m, n;
        if (matrix == null || (m = matrix.length) == 0 || matrix[0] == null || (n = matrix[0].length) == 0) return false;
        int i = 0, j = n - 1;
        while (i < m && j >= 0) {
     
            if (matrix[i][j] == target) return true;
            if (matrix[i][j] > target) --j;
            else ++i;
        }
        return false;
    }
}

JavaScript

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var findNumberIn2DArray = function (matrix, target) {
     
  let row = matrix.length;
  let col = matrix[0].length;
  function dfs(i, j) {
     
    if (i < 0 || j >= col) {
     
      return false;
    }
    if (matrix[i][j] === target) return true;
    else if (matrix[i][j] > target) {
     
      return dfs(i - 1, j);
    } else {
     
      return dfs(i, j + 1);
    }
  }
  return dfs(row - 1, 0);
};

Go

func findNumberIn2DArray(matrix [][]int, target int) bool {
     
    if len(matrix) == 0 {
     
        return false
    }
    rows, cols := len(matrix), len(matrix[0])
    i, j := rows - 1, 0
    for i >= 0 && j < cols {
     
        if matrix[i][j] == target {
     
            return true
        }
        if matrix[i][j] > target {
     
            i--
        } else {
     
            j++
        }
    }
    return false
}

…

面试题 05. 替换空格

题目描述

请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

示例 1：

输入：s = "We are happy."
输出："We%20are%20happy."

限制：

0 <= s 的长度 <= 10000

解法

使用 replace 替换即可。

Python3

class Solution:
    def replaceSpace(self, s: str) -> str:
        return s.replace(' ', '%20')

Java

使用 replace：

class Solution {
     
    public String replaceSpace(String s) {
     
        return s.replaceAll(" ", "%20");
    }
}

使用 StringBuilder：

class Solution {
     
    public String replaceSpace(String s) {
     
        StringBuilder sb = new StringBuilder();
        char[] chars = s.toCharArray();
        for (char c : chars) {
     
            sb.append(c == ' ' ? "%20" : c);
        }
        return sb.toString();
    }
}

JavaScript

/**
 * @param {string} s
 * @return {string}
 */
var replaceSpace = function (s) {
     
  return s.split(" ").join("%20");
};

Go

func replaceSpace(s string) string {
     
    return strings.Replace(s, " ", "%20", -1 )
}

…

面试题 06. 从尾到头打印链表

题目描述

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

示例 1：

输入：head = [1,3,2]
输出：[2,3,1]

限制：

0 <= 链表长度 <= 10000

解法

栈实现。或者其它方式，见题解。

Python3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def reversePrint(self, head: ListNode) -> List[int]:
        res = []
        while head:
            res.append(head.val)
            head = head.next
        return res[::-1]

Java

栈实现：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public int[] reversePrint(ListNode head) {
     
        Stack<Integer> s = new Stack<>();
        while (head != null) {
     
            s.push(head.val);
            head = head.next;
        }
        int[] res = new int[s.size()];
        int i = 0;
        while (!s.isEmpty()) {
     
            res[i++] = s.pop();
        }
        return res;
    }
}

先计算链表长度 n，然后创建一个长度为 n 的结果数组。最后遍历链表，依次将节点值存放在数组上（从后往前）。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public int[] reversePrint(ListNode head) {
     
        if (head == null) return new int[]{
     };
        // 计算链表长度n
        int n = 0;
        ListNode cur = head;
        while (cur != null) {
     
            ++n;
            cur = cur.next;
        }
        int[] res = new int[n];
        cur = head;
        while (cur != null) {
     
            res[--n] = cur.val;
            cur = cur.next;
        }
        return res;
    }
}

Go

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
//insert to the front
func reversePrint(head *ListNode) []int {
     
	res := []int{
     }
	for head != nil {
     
		res = append([]int{
     head.Val}, res...)
		head = head.Next
	}
	return res
}

C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
     
public:
    vector<int> ret;

    void getVal(ListNode* head) {
     
        // 这里可以看成是一个节点的树
        if (head) {
     
            if (head->next) {
     
                getVal(head->next);
            }
            ret.push_back(head->val);
        }
    }

    vector<int> reversePrint(ListNode* head) {
     
        getVal(head);
        // 返回的是全局的ret信息。在getVal函数中被赋值
        return ret;
    }
};

…

面试题 07. 重建二叉树

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

限制：

0 <= 节点个数 <= 5000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    indexes = {
     }
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def build(preorder, inorder, p1, p2, i1, i2) -> TreeNode:
            if p1 > p2 or i1 > i2:
                return None
            root_val = preorder[p1]
            pos = self.indexes[root_val]
            root = TreeNode(root_val)
            root.left = None if pos == i1 else build(preorder, inorder, p1 + 1, p1 - i1 + pos, i1, pos - 1)
            root.right = None if pos == i2 else build(preorder, inorder, p1 - i1 + pos + 1, p2, pos + 1, i2)
            return root
        n = len(inorder)
        for i in range(n):
            self.indexes[inorder[i]] = i
        return build(preorder, inorder, 0, n - 1, 0, n - 1)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    private Map<Integer, Integer> indexes = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
     
        int n = inorder.length;
        for (int i = 0; i < n; ++i) {
     
            indexes.put(inorder[i], i);
        }
        return build(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    private TreeNode build(int[] preorder, int[] inorder, int p1, int p2, int i1, int i2) {
     
        if (p1 > p2 || i1 > i2) return null;
        int rootVal = preorder[p1];
        int pos = indexes.get(rootVal);
        TreeNode node = new TreeNode(rootVal);
        node.left = pos == i1 ? null : build(preorder, inorder, p1 + 1, pos - i1 + p1, i1, pos - 1);
        node.right = pos == i2 ? null : build(preorder, inorder, pos - i1 + p1 + 1, p2, pos + 1, i2);
        return node;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function (preorder, inorder) {
     
  if (!preorder || !preorder.length) return null;
  let preIdx = 0;
  let inMap = {
     };
  for (let i = 0; i < inorder.length; i++) {
     
    inMap[inorder[i]] = i;
  }
  function func(start, end) {
     
    if (start > end) {
     
      return null;
    }
    let preVal = preorder[preIdx];
    preIdx++;
    let inIdx = inMap[preVal];
    let node = new TreeNode(preVal);
    node.left = func(start, inIdx - 1);
    node.right = func(inIdx + 1, end);
    return node;
  }
  return func(0, preorder.length - 1);
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(preorder []int, inorder []int) *TreeNode {
     
    return helper(preorder, inorder, 0, 0, len(preorder)-1)
}

func helper(preorder, inorder []int, index, start, end int) *TreeNode {
     
    if start > end {
     
        return nil
    }
    root := &TreeNode{
     Val:preorder[index]}
    j := start
    for j < end && preorder[index] != inorder[j] {
     
        j++
    }
    root.Left = helper(preorder, inorder, index + 1, start, j - 1)
    root.Right = helper(preorder, inorder, index + 1 + j -start, j + 1, end)
    return root
}

…

面试题 09. 用两个栈实现队列

题目描述

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入：
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出：[null,null,3,-1]

示例 2：

输入：
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]
输出：[null,-1,null,null,5,2]

提示：

1 <= values <= 10000
最多会对 appendTail、deleteHead 进行 10000 次调用

解法

Python3

class CQueue:

    def __init__(self):
        self.s1 = []
        self.s2 = []

    def appendTail(self, value: int) -> None:
        self.s1.append(value)
        if not self.s2:
            self._move()

    def deleteHead(self) -> int:
        if not self.s2:
            self._move()
        return -1 if not self.s2 else self.s2.pop()

    def _move(self):
        while self.s1:
            self.s2.append(self.s1.pop())



# Your CQueue object will be instantiated and called as such:
# obj = CQueue()
# obj.appendTail(value)
# param_2 = obj.deleteHead()

Java

class CQueue {
     

    private Deque<Integer> s1;
    private Deque<Integer> s2;
    public CQueue() {
     
        s1 = new ArrayDeque<>();
        s2 = new ArrayDeque<>();
    }

    public void appendTail(int value) {
     
        s1.push(value);
        if (s2.isEmpty()) {
     
            move();
        }
    }

    public int deleteHead() {
     
        if (s2.isEmpty()) {
     
            move();
        }
        return s2.isEmpty() ? -1 : s2.pop();
    }

    private void move() {
     
        while (!s1.isEmpty()) {
     
            s2.push(s1.pop());
        }
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */

JavaScript

var CQueue = function () {
     
  this.data = [];
  this.helper = [];
};
/**
 * @param {number} value
 * @return {void}
 */
CQueue.prototype.appendTail = function (value) {
     
  this.data.push(value);
};
/**
 * @return {number}
 */
CQueue.prototype.deleteHead = function () {
     
  if (this.data.length) {
     
    while (this.data.length > 1) {
     
      this.helper.push(this.data.pop());
    }
    let res = this.data.pop();
    while (this.helper.length) {
     
      this.data.push(this.helper.pop());
    }
    return res;
  } else {
     
    return -1;
  }
};

Go

type CQueue struct {
     
	Stack1 []int
	Stack2 []int
}

// 入队都往S1压入，弹出时判定S2是否为空，S2非空则弹出S2顶，否则，S1的元素从栈顶依次入S2
//再从S2弹出

func Constructor() CQueue {
     
	return CQueue{
     Stack1: []int{
     }, Stack2: []int{
     }}
}

func (this *CQueue) AppendTail(value int) {
     
	this.Stack1 = append(this.Stack1, value)
}

func (this *CQueue) DeleteHead() int {
     
	if len(this.Stack1) == 0 && len(this.Stack2) == 0 {
     
		return -1
	}
	if len(this.Stack2) > 0 {
     
		res := this.Stack2[len(this.Stack2)-1]
		this.Stack2 = this.Stack2[0 : len(this.Stack2)-1]
		return res
	}
	for len(this.Stack1) > 0 {
     
		this.Stack2 = append(this.Stack2, this.Stack1[len(this.Stack1)-1])
		this.Stack1 = this.Stack1[0 : len(this.Stack1)-1]
	}
	res := this.Stack2[len(this.Stack2)-1]
	this.Stack2 = this.Stack2[0 : len(this.Stack2)-1]
	return res
}

…

面试题 10- I. 斐波那契数列

题目描述

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：1

示例 2：

输入：n = 5
输出：5

提示：

0 <= n <= 100

解法

递推求解。

Python3

class Solution:
    def fib(self, n: int) -> int:
        a, b = 0, 1
        for _ in range(n):
            a, b = b, a + b
        return a % 1000000007

Java

class Solution {
     
    public int fib(int n) {
     
        int a = 0, b = 1;
        for (int i = 0; i < n; ++i) {
     
            int c = (a + b) % 1000000007;
            a = b;
            b = c;
        }
        return a;
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var fib = function (n) {
     
  if (!n) return 0;
  let pre = 0;
  let cur = 1;
  for (let i = 2; i <= n; i++) {
     
    let c = (pre + cur) % (1e9 + 7);
    pre = cur;
    cur = c;
  }
  return cur;
};

Go

func fib(n int) int {
     
    if n < 2 {
     
        return n
    }
    a := make([]int,n+1)
    a[0]=0
    a[1]=1
    for i := 2; i < n+1; i++ {
     
        a[i] = (a[i-1]+ a[i-2])%1000000007
    }
    return a[n]
}

…

面试题 10- II. 青蛙跳台阶问题

题目描述

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2

示例 2：

输入：n = 7
输出：21

提示：

0 <= n <= 100

解法

青蛙想上第 n 级台阶，可从第 n-1 级台阶跳一级上去，也可从第 n-2 级台阶跳两级上去，即：f(n) = f(n-1) + f(n-2)。递推求解即可。

Python3

class Solution:
    def numWays(self, n: int) -> int:
        a, b = 0, 1
        for _ in range(n):
            a, b = b, a + b
        return b % 1000000007

Java

class Solution {
     
    public int numWays(int n) {
     
        int a = 0, b = 1;
        for (int i = 0; i < n; ++i) {
     
            int s = (a + b) % 1000000007;
            a = b;
            b = s;
        }
        return b;
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var numWays = function (n) {
     
  if (!n) return 1;
  let pre = 1;
  let cur = 1;
  for (let i = 2; i <= n; i++) {
     
    let c = (pre + cur) % (1e9 + 7);
    pre = cur;
    cur = c;
  }
  return cur;
};

Go

func numWays(n int) int {
     
	if n == 0 {
     
		return 1
	}
	if n <= 2 {
     
		return n
	}
	a := make([]int, n)
	a[0] = 1
	a[1] = 2
	for i := 2; i < n; i++ {
     
		a[i] = (a[i-1] + a[i-2]) % 1000000007
	}
	return a[n-1]
}

…

面试题 11. 旋转数组的最小数字

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为 1。

示例 1：

输入：[3,4,5,1,2]
输出：1

示例 2：

输入：[2,2,2,0,1]
输出：0

解法

Python3

class Solution:
    def minArray(self, numbers: List[int]) -> int:
        l, r = 0, len(numbers) - 1
        while l < r:
            m = l + ((r - l) >> 1)
            if numbers[m] > numbers[r]:
                l = m + 1
            elif numbers[m] < numbers[r]:
                r = m
            else:
                r -= 1
        return numbers[l]

Java

class Solution {
     
    public int minArray(int[] numbers) {
     
        int l = 0, r = numbers.length - 1;
        while (l < r) {
     
            int m = l + ((r - l) >> 1);
            if (numbers[m] > numbers[r]) {
     
                l = m + 1;
            } else if (numbers[m] < numbers[r]) {
     
                r = m;
            } else {
     
                --r;
            }
        }
        return numbers[l];
    }
}

JavaScript

/**
 * @param {number[]} numbers
 * @return {number}
 */
var minArray = function (numbers) {
     
  // return Math.min(...numbers)
  let left = 0;
  let right = numbers.length - 1;
  while (left < right) {
     
    let mid = left + ~~((right - left) / 2);
    if (numbers[mid] > numbers[right]) {
     
      left = mid + 1;
    } else if (numbers[mid] === numbers[right]) {
     
      right--;
    } else {
     
      right = mid;
    }
  }
  return numbers[left];
};

Go

func minArray(nums []int) int {
     
	l, r := 0, len(nums)-1
	for l < r {
     
		mid := l + (r-l)>>1
		if nums[mid] > nums[r] {
     
			l = mid + 1
		} else if nums[mid] < nums[r] {
     
			r = mid //r 本身不需要被排除
		} else {
     
			r--
		}
	}
	return nums[l]
}

…

面试题 12. 矩阵中的路径

题目描述

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如，在下面的 3×4 的矩阵中包含一条字符串“bfce”的路径（路径中的字母用加粗标出）。

[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]

但矩阵中不包含字符串“abfb”的路径，因为字符串的第一个字符 b 占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

提示：

1 <= board.length <= 200
1 <= board[i].length <= 200

解法

深度优先搜索 DFS 解决。

Python3

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        def dfs(i, j, cur):
            if cur == len(word):
                return True
            if i < 0 or i >= m or j < 0 or j >= n or visited[i][j] or word[cur] != board[i][j]:
                return False
            visited[i][j] = True
            next = cur + 1
            res = dfs(i + 1, j, next) or dfs(i - 1, j, next) or dfs(i, j + 1, next) or dfs(i, j - 1, next)
            visited[i][j] = False
            return res
        m, n = len(board), len(board[0])
        visited = [[False for _ in range(n)] for _ in range(m)]
        for i in range(m):
            for j in range(n):
                res = dfs(i, j, 0)
                if res:
                    return True
        return False

Java

class Solution {
     
    private boolean[][] visited;

    public boolean exist(char[][] board, String word) {
     
        int m = board.length, n = board[0].length;
        visited = new boolean[m][n];
        char[] chars = word.toCharArray();
        for (int i = 0; i < m; ++i) {
     
            for (int j = 0; j < n; ++j) {
     
                boolean res = dfs(board, i, j, chars, 0);
                if (res) return true;
            }
        }
        return false;
    }

    private boolean dfs(char[][] board, int i, int j, char[] chars, int cur) {
     
        if (cur == chars.length) return true;
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length) return false;
        if (visited[i][j] || board[i][j] != chars[cur]) return false;
        visited[i][j] = true;
        int next = cur + 1;
        boolean res = dfs(board, i + 1, j, chars, next)
                || dfs(board, i - 1, j, chars, next)
                || dfs(board, i, j + 1, chars, next)
                || dfs(board, i, j - 1, chars, next);
        visited[i][j] = false;
        return res;
    }
}

JavaScript

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function (board, word) {
     
  let row = board.length;
  let col = board[0].length;
  let res = false;
  let isRead = [...new Array(row)].map(() => Array(col).fill(0));
  for (let i = 0; i < row; i++) {
     
    for (let j = 0; j < col; j++) {
     
      if (res) break;
      if (board[i][j] === word[0]) {
     
        dfs(i, j, word);
      }
    }
  }
  function dfs(i, j, word) {
     
    if (
      i < 0 ||
      j < 0 ||
      i >= row ||
      j >= col ||
      res ||
      isRead[i][j] ||
      board[i][j] !== word[0]
    ) {
     
      return;
    }
    isRead[i][j] = 1;
    word = word.substring(1);
    if (word.length) {
     
      dfs(i - 1, j, word);
      dfs(i + 1, j, word);
      dfs(i, j - 1, word);
      dfs(i, j + 1, word);
    } else {
     
      res = true;
      return;
    }
    isRead[i][j] = 0;
  }
  return res;
};

Go

func exist(board [][]byte, word string) bool {
     
	if len(board) == 0 {
     
		return false
	}
	//标记数组
	isVisited := make([][]bool, len(board))
	for i := 0; i < len(board); i++ {
     
		isVisited[i] = make([]bool, len(board[0]))
	}
	for i := 0; i < len(board); i++ {
     
		for j := 0; j < len(board[0]); j++ {
     
			if board[i][j] == word[0] {
     
				if bfs(board, i, j, isVisited, word, 0) {
     
					return true
				}
			}
		}
	}
	return false
}

func bfs(board [][]byte, i, j int, isVisited [][]bool, word string, index int) bool {
     
	if index == len(word) {
     
		return true
	}
	if i < 0 || j < 0 || i == len(board) || j == len(board[0]) || isVisited[i][j] || board[i][j] != word[index] {
     
		return false
	}
	isVisited[i][j] = true
	res := bfs(board, i+1, j, isVisited, word, index+1) ||
		bfs(board, i, j+1, isVisited, word, index+1) ||
		bfs(board, i-1, j, isVisited, word, index+1) ||
		bfs(board, i, j-1, isVisited, word, index+1)
	isVisited[i][j] = false
	return res
}

C++

class Solution {
     
public:
    bool dfs(vector<vector<char>>& board, string& word, int cur, int x, int y) {
     
        if (board[x][y] != word[cur]) {
     
            return false;
        }

        if (cur == word.size()-1) {
     
            return true;
        }

        char t = board[x][y];
        board[x][y] = '*';    // 表示查询过了这个字段
        int dx[4] = {
     -1, 0, 1, 0};
        int dy[4] = {
     0, 1, 0, -1};
        for (int k = 0; k < 4; k++) {
     
            // 从上、右、下、左四个方向，开始dfs
            int a = x + dx[k], b = y + dy[k];
            if (a >= 0 && a < board.size() && b >= 0 && b < board[0].size()) {
     
                if (dfs(board, word, cur+1, a, b)) {
     
                    return true;
                }
            }
        }

        board[x][y] = t;
        return false;
    }

    bool exist(vector<vector<char>>& board, string word) {
     
        int x = board.size();
        int y = board[0].size();
        if (0 == x || 0 == y) {
     
            return false;
        }

        for (int i = 0; i < x; i++) {
     
            for (int j = 0; j < y; j++) {
     
                if (dfs(board, word, 0, i, j)) {
     
                    return true;
                }
            }
        }

        return false;
    }
};

…

面试题 13. 机器人的运动范围

题目描述

地上有一个 m 行 n 列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于 k 的格子。例如，当 k 为 18 时，机器人能够进入方格 [35, 37] ，因为 3+5+3+7=18。但它不能进入方格 [35, 38]，因为 3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

输入：m = 2, n = 3, k = 1
输出：3

示例 2：

输入：m = 3, n = 1, k = 0
输出：1

提示：

1 <= n,m <= 100
0 <= k <= 20

解法

深度优先搜索 DFS 实现。

Python3

class Solution:
    cnt = 0
    def movingCount(self, m: int, n: int, k: int) -> int:
        def cal(m, n):
            s = str(m) + str(n)
            return sum([int(i) for i in s])
        def dfs(i, j):
            if i < 0 or i >= m or j < 0 or j >= n or cal(i, j) > k or visited[i][j]:
                return
            self.cnt += 1
            visited[i][j] = True
            dfs(i + 1, j)
            dfs(i - 1, j)
            dfs(i, j + 1)
            dfs(i, j - 1)
        self.cnt = 0
        visited = [[False for _ in range(n)] for _ in range(m)]
        dfs(0, 0)
        return self.cnt

Java

class Solution {
     
    private int m;
    private int n;
    private boolean[][] visited;
    private int cnt;
    public int movingCount(int m, int n, int k) {
     
        visited = new boolean[m][n];
        this.m = m;
        this.n = n;
        cnt = 0;
        dfs(0, 0, k);
        return cnt;
    }

    private void dfs(int i, int j, int k) {
     
        if (i < 0 || i >= m || j < 0 || j >= n || visited[i][j] || cal(i, j) > k) return;
        ++cnt;
        visited[i][j] = true;
        dfs(i + 1, j, k);
        dfs(i - 1, j, k);
        dfs(i, j + 1, k);
        dfs(i, j - 1, k);
    }

    private int cal(int i, int j) {
     
        int res = 0;
        while (i != 0) {
     
            res += (i % 10);
            i /= 10;
        }
        while (j != 0) {
     
            res += (j % 10);
            j /= 10;
        }
        return res;
    }
}

JavaScript

/**
 * @param {number} m
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
var movingCount = function (m, n, k) {
     
  let res = 0;
  let isRead = [...new Array(m)].map(() => Array(n).fill(0));
  let moving = [
    [0, -1],
    [0, 1],
    [1, 0],
    [-1, 0],
  ];
  let queue = [[0, 0]];
  isRead[0][0] = 1;
  while (queue.length) {
     
    let [x, y] = queue.shift();
    for (let [dx, dy] of moving) {
     
      let X = x + dx;
      let Y = y + dy;
      if (
        X >= 0 &&
        Y >= 0 &&
        X < m &&
        Y < n &&
        !isRead[X][Y] &&
        isValid(X, Y)
      ) {
     
        queue.push([X, Y]);
        isRead[X][Y] = 1;
      }
    }
    res++;
  }
  function isValid(x, y) {
     
    let r = 0;
    r +=
      x
        .toString()
        .split("")
        .reduce((acc, cur) => acc + +cur, 0) +
      y
        .toString()
        .split("")
        .reduce((acc, cur) => acc + +cur, 0);
    if (r <= k) return true;
    else return false;
  }
  return res;
};

Go

func movingCount(m int, n int, k int) int {
     
	var visited [][]bool
	visited = make([][]bool, m)
	for i := 0; i < m; i++ {
     
		visited[i] = make([]bool, n)
	}
	return dfs(0, 0, m, n, k, visited)
}

func dfs(x, y, m, n, k int, visited [][]bool) int {
     
	if x >= m || y >= n || visited[x][y] || (x%10+x/10+y%10+y/10) > k {
     
		return 0
	}
	visited[x][y] = true
	return 1 + dfs(x+1, y, m, n, k, visited) + dfs(x, y+1, m, n, k, visited)
}

C++

class Solution {
     
public:
    int checksum(int m, int n, int target) {
     
        int a = 0;
        while (m > 0) {
     
            a += m % 10;
            m /= 10;
        }

        int b = 0;
        while (n > 0) {
     
            b += n % 10;
            n /= 10;
        }

        return a + b <= target;
    }

    int moving(int row, int col, vector<vector<int>>& arr, int i, int j, int target) {
     
        int count = 0;
        if (checksum(i, j, target)
            && i>=0 && i < row && j>=0 && j < col
            && arr[i][j] == 0) {
     
            arr[i][j] = 1;
            count = 1 + moving(row, col, arr, i-1, j, target)
                    + moving(row, col, arr, i, j-1, target)
                    + moving(row, col, arr, i+1, j, target)
                    + moving(row, col, arr, i, j+1, target);
        }

        return count;
    }

    int movingCount(int m, int n, int k) {
     
        if (m == 0 || n == 0) {
     
            return 0;
        }

        vector<vector<int>> arr(m, vector<int>(n, 0));
        int cnt = moving(m, n, arr, 0, 0, k);
        return cnt;
    }
};

…

面试题 14- I. 剪绳子

题目描述

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n 都是整数，n>1 并且 m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是 8 时，我们把它剪成长度分别为 2、3、3 的三段，此时得到的最大乘积是 18。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

2 <= n <= 58

解法

尽可能将绳子以长度 3 等分剪为多段时，乘积最大。

Python3

class Solution:
    def cuttingRope(self, n: int) -> int:
        if n < 4:
            return n - 1
        res = 1
        while n > 4:
            res *= 3
            n -= 3
        if n == 4:
            return res << 2
        return res * n

Java

class Solution {
     
    public int cuttingRope(int n) {
     
        if (n < 4) return n - 1;
        int res = 1;
        while (n > 4) {
     
            res *= 3;
            n -= 3;
        }
        if (n == 4) return res << 2;
        return res * n;
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var cuttingRope = function (n) {
     
  // 数学方法
  if (n <= 3) return n - 1;
  let a = ~~(n / 3);
  let b = n % 3;
  if (b === 1) {
     
    return 3 ** (a - 1) * 2 * 2;
  }
  if (b === 0) return 3 ** a;
  return 3 ** a * b;
  // dp 方法
  // let dp = new Array(n+1).fill(0)
  // dp[0] = 1
  // for(let i=1;i
  //     for(let j=i;j<=n;j++) {
     
  //         dp[j] = Math.max(dp[j],dp[j-i] * i)
  //     }
  // }
  // return dp[n]
};

Go

func cuttingRope(n int) int {
     
	if n <= 3 {
     
		return n - 1
	}
	sum := 1
	for n > 4 {
     
		sum *= 3
		n -= 3
	}
	return sum * n
}

…

面试题 14- II. 剪绳子 II

题目描述

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

提示：

2 <= n <= 1000

解法

Python3

class Solution:
    def cuttingRope(self, n: int) -> int:
        if n < 4:
            return n - 1
        res = 1
        while n > 4:
            res *= 3
            n -= 3
        if n == 4:
            return (res << 2) % 1000000007
        return (res * n) % 1000000007

Java

class Solution {
     
    public int cuttingRope(int n) {
     
        if (n < 4) {
     
            return n - 1;
        }
        int s1 = n / 3;
        int m = n % 3;
        if (m == 1) {
     
            s1 -= 1;
            m = 4;
        }
        long res = 1;
        while (s1-- > 0) {
     
            res *= 3;
            res %= 1000000007;
        }
        return (int) ((res * (m == 0 ? 1 : m)) % 1000000007);
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var cuttingRope = function (n) {
     
  if (n <= 3) return n - 1;
  let a = ~~(n / 3);
  let b = n % 3;
  const MOD = 1e9 + 7;
  function myPow(x) {
     
    let r = 1;
    for (let i = 0; i < x; i++) {
     
      r = (r * 3) % MOD;
    }
    return r;
  }
  if (b === 1) {
     
    return (myPow(a - 1) * 4) % MOD;
  }
  if (b === 0) return myPow(a) % MOD;
  return (myPow(a) * 2) % MOD;
};

Go

func cuttingRope(n int) int {
     
	if n <= 3 {
     
		return n - 1
	}
	sum := 1
	for n > 4 {
     
		sum *= 3
		sum = sum % 1000000007
		n -= 3
	}
	return sum * n % 1000000007
}

…

面试题 15. 二进制中 1 的个数

题目描述

请实现一个函数，输入一个整数，输出该数二进制表示中 1 的个数。例如，把 9 表示成二进制是 1001，有 2 位是 1。因此，如果输入 9，则该函数输出 2。

示例 1：

输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

示例 2：

输入：00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

示例 3：

输入：11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

解法

n & (n - 1) 会消除 n 中最后一位中的 1。

Python3

class Solution:
    def hammingWeight(self, n: int) -> int:
        res = 0
        while n:
            n &= (n - 1)
            res += 1
        return res

Java

public class Solution {
     
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
     
        int res = 0;
        while (n != 0) {
     
            n &= (n - 1);
            ++res;
        }
        return res;
    }
}

JavaScript

/**
 * @param {number} n - a positive integer
 * @return {number}
 */
var hammingWeight = function (n) {
     
  let cnt = 0;
  while (n) {
     
    cnt += n & 1;
    n >>>= 1;
  }
  return cnt;
};

Go

func hammingWeight(num uint32) int {
     
	ans := 0
	// num &=num-1 消除最右边的1
	for num != 0 {
     
		num &= num - 1
		ans++
	}
	return ans
}

…

面试题 16. 数值的整数次方

题目描述

实现函数 double Power(double base, int exponent)，求 base 的 exponent 次方。不得使用库函数，同时不需要考虑大数问题。

示例 1:

输入: 2.00000, 10
输出: 1024.00000

示例 2:

输入: 2.10000, 3
输出: 9.26100

示例 3:

输入: 2.00000, -2
输出: 0.25000
解释: 2-2 = 1/22 = 1/4 = 0.25

说明:

-100.0 < x < 100.0
n 是 32 位有符号整数，其数值范围是 [−231, 231 − 1] 。

解法

Python3

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if n == 0:
            return 1
        if n == 1:
            return x
        if n == -1:
            return 1 / x
        half = self.myPow(x, n // 2)
        return half * half * self.myPow(x, n % 2)

Java

class Solution {
     
    public double myPow(double x, int n) {
     
        if (n == 0) return 1;
        if (n == 1) return x;
        if (n == -1) return 1 / x;
        double half = myPow(x, n / 2);
        return half * half * myPow(x, n % 2);
    }
}

JavaScript

/**
 * @param {number} x
 * @param {number} n
 * @return {number}
 */
var myPow = function (x, n) {
     
  let r = 1;
  let tmp = x;
  let tag = 0;
  if (n < 0) {
     
    tag = 1;
    n = -n;
  }
  while (n) {
     
    if (n & 1) {
     
      r *= tmp;
    }
    tmp *= tmp;
    n >>>= 1;
  }
  return tag ? 1 / r : r;
};

Go

func myPow(x float64, n int) float64 {
     
    p := abs(n)
    res := 1.0
    for p != 0 {
     
        if p&1 == 1 {
     
            res *= x
        }
        x *= x
        p = p >>1
    }
    if n < 0 {
     
        return 1/res
    }
    return res
}

func abs(x int) int {
     
    if x > 0 {
     
        return x
    }
    return -x
}

…

面试题 17. 打印从 1 到最大的 n 位数

题目描述

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1:

输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]

说明：

用返回一个整数列表来代替打印
n 为正整数

解法

Python3

class Solution:
    def printNumbers(self, n: int) -> List[int]:
        return [i for i in range(1, 10 ** n)]

Java

class Solution {
     
    public int[] printNumbers(int n) {
     
        n = (int) Math.pow(10, n) - 1;
        int[] res = new int[n];
        for (int i = 0; i < n; ++i) {
     
            res[i] = i + 1;
        }
        return res;
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number[]}
 */
var printNumbers = function (n) {
     
  let res = [];
  for (let i = 1; i < 10 ** n; ++i) {
     
    res.push(i);
  }
  return res;
};

Go

func printNumbers(n int) []int {
     
    d := 10
    for i := 1; i < n; i++ {
     
        d *= 10
    }
    res := make([]int, d - 1)
    for i := 1; i < d; i++ {
     
        res[i - 1] = i
    }
    return res
}

…

面试题 18. 删除链表的节点

题目描述

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。

返回删除后的链表的头节点。

注意：此题对比原题有改动。

示例 1:

输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

示例 2:

输入: head = [4,5,1,9], val = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 4 -> 5 -> 9.

说明：

题目保证链表中节点的值互不相同
若使用 C 或 C++ 语言，你不需要 free 或 delete 被删除的节点

解法

定义一个虚拟头节点 dummy 指向 head，pre 指针初始指向 dummy。

循环遍历链表，pre 往后移动。当指针 pre.next 指向的节点的值等于 val 时退出循环，将 pre.next 指向 pre.next.next，然后返回 dummy.next。

Python3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def deleteNode(self, head: ListNode, val: int) -> ListNode:
        dummy = ListNode(0)
        dummy.next = head
        pre = dummy
        while pre.next and pre.next.val != val:
            pre = pre.next
        pre.next = None if not pre.next else pre.next.next
        return dummy.next

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public ListNode deleteNode(ListNode head, int val) {
     
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode pre = dummy;
        while (pre.next != null && pre.next.val != val) {
     
            pre = pre.next;
        }
        pre.next = pre.next == null ? null : pre.next.next;
        return dummy.next;
    }
}

JavaScript

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @param {number} val
 * @return {ListNode}
 */
var deleteNode = function (head, val) {
     
  const dummy = new ListNode(0);
  dummy.next = head;
  let pre = dummy;
  while (pre.next && pre.next.val != val) {
     
    pre = pre.next;
  }
  pre.next = pre.next ? pre.next.next : null;
  return dummy.next;
};

Go

func deleteNode(head *ListNode, val int) *ListNode {
     
    res := &ListNode{
     
        Val: 0,
        Next: head,
    }
    pre := res
    cur := res.Next
    for cur != nil {
     
        if cur.Val == val {
     
            pre.Next = cur.Next
            return res.Next
        }
        cur = cur.Next
        pre = pre.Next
    }
    return res.Next
}

C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
     
public:
    ListNode* deleteNode(ListNode* head, int val) {
     
        ListNode* cur = head;
        if (!head) {
     
            return nullptr;
        }

        if (head->val == val) {
     
            // 第一个就匹配的情况
            return head->next;
        }

        while (cur && cur->next) {
     
            if (cur->next->val == val) {
     
                // 如果找到了，直接指向下一个
                cur->next = cur->next->next;
                break;
            } else {
     
                cur = cur->next;
            }
        }

        return head;
    }
};

…

面试题 19. 正则表达式匹配

题目描述

请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符，而'*'表示它前面的字符可以出现任意次（含 0 次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab*ac*a"匹配，但与"aa.a"和"ab*a"均不匹配。

示例 1:

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3:

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

示例 4:

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

示例 5:

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

解法

动态规划法，dp[i][j] 表示 s 的前 i 项和 p 的前 j 项是否匹配。

现在如果已知了 dp[i-1][j-1] 的状态，我们该如何确定 dp[i][j] 的状态呢？我们可以分三种情况讨论，其中，前两种情况考虑了所有能匹配的情况，剩下的就是不能匹配的情况了：

s[i] == p[j] or p[j] == '.'：比如 abb 和 abb，或者 abb 和 ab. ，很容易得到 dp[i][j] = dp[i-1][j-1] = True。因为 ab 和 ab 是匹配的，如果后面分别加一个 b，或者 s 加一个 b 而 p 加一个 . ，仍然是匹配的。
p[j] == '*'：当 p[j] == '*' 时，由于 * 与前面的字符相关，因此我们比较 * 前面的字符 p[j-1] 和 s[i] 的关系。根据 * 前面的字符与 s[i] 是否相等，又可分为以下两种情况：
- p[j-1] != s[i]：如果 * 前一个字符匹配不上，* 匹配了 0 次，应忽略这两个字符，看 p[j-2] 和 s[i] 是否匹配。这时 dp[i][j] = dp[i][j-2]。
- p[j-1] == s[i] or p[j-1] == '.'：* 前面的字符可以与 s[i] 匹配，这种情况下，* 可能匹配了前面的字符的 0 个，也可能匹配了前面字符的多个，当匹配 0 个时，如 ab 和 abb*，或者 ab 和 ab.* ，这时我们需要去掉 p 中的 b* 或 .* 后进行比较，即 dp[i][j] = dp[i][j-2]；当匹配多个时，如 abbb 和 ab*，或者 abbb 和 a.*，我们需要将 s[i] 前面的与 p 重新比较，即 dp[i][j] = dp[i-1][j]。
其他情况：以上两种情况把能匹配的都考虑全面了，所以其他情况为不匹配，即 dp[i][j] = False。

Python3

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        m, n = len(s) + 1, len(p) + 1
        if n == 1:
            return m == 1
        dp = [[False for _ in range(n)] for _ in range(m)]
        dp[0][0], dp[0][1] = True, False
        for j in range(2, n):
            if p[j - 1] == '*':
                dp[0][j] = dp[0][j - 2]
        for i in range(1, m):
            for j in range(1, n):
                if s[i - 1] == p[j - 1] or p[j - 1] == '.':
                    dp[i][j] = dp[i - 1][j - 1]
                elif p[j - 1] == '*':
                    if p[j - 2] == '.' or p[j - 2] == s[i - 1]:
                        dp[i][j] = dp[i][j - 2] or dp[i - 1][j]
                    else:
                        dp[i][j] = dp[i][j - 2]
                else:
                    dp[i][j] = False
        return dp[m - 1][n - 1]

Java

class Solution {
     
    public boolean isMatch(String s, String p) {
     
        int m = s.length() + 1, n = p.length() + 1;
        if (n == 1) {
     
            return m == 1;
        }
        boolean[][] dp = new boolean[m + 1][n + 1];
        dp[0][0] = true;
        dp[0][1] = false;
        for (int j = 1; j < n; ++j) {
     
            if (p.charAt(j - 1) == '*') {
     
                dp[0][j] = dp[0][j - 2];
            }
        }
        for (int i = 1; i < m; ++i) {
     
            for (int j = 1; j < n; ++j) {
     
                if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
     
                    dp[i][j] = dp[i - 1][j - 1];
                } else if (p.charAt(j - 1) == '*') {
     
                    if (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') {
     
                        dp[i][j] = dp[i][j - 2] || dp[i - 1][j];
                    } else {
     
                        dp[i][j] = dp[i][j - 2];
                    }
                } else {
     
                    dp[i][j] = false;
                }
            }
        }
        return dp[m - 1][n - 1];
    }
}

JavaScript

/**
 * @param {string} s
 * @param {string} p
 * @return {boolean}
 */
var isMatch = function (s, p) {
     
  // 回溯大法好
  let memo = {
     };
  function recursive(i, j) {
     
    if (memo[[i, j]] !== undefined) return memo[[i, j]];
    if (j === p.length) return i === s.length;
    let tmp = i < s.length && (s[i] === p[j] || p[j] === ".");
    let ans = false;
    if (p[j + 1] === "*") {
     
      ans = recursive(i, j + 2) || (tmp && recursive(i + 1, j));
    } else {
     
      ans = tmp && recursive(i + 1, j + 1);
    }
    memo[[i, j]] = ans;
    return ans;
  }
  return recursive(0, 0);
};

C++

class Solution {
     
public:
    bool match(string s, string p, int sl, int pl) {
     
        /* 说明：sl指的是s的len，pl指的是p的len。
           使用这种写法，在牛客上是能ac的。在leetcode上会显示特定的用例超时。
           写在这里，给大家提供一种新的思路吧。
           二维动态规划应该更适合做这一题的题解（参考java版本答案） */
        if (sl == s.size() && pl == p.size()) {
     
            return true;
        }

        if (sl < s.size() && pl == p.size()) {
     
            return false;
        }

        if (p[pl+1] != '*') {
     
            // 如果p的下一个不是*的情况
            if ((s[sl] == p[pl]) || (sl<s.size() && p[pl] == '.')) {
     
                return match(s, p, sl+1, pl+1);
            } else {
     
                return false;
            }
        } else {
     
            if ((s[sl] == p[pl]) || (sl<s.size() && p[pl] == '.')) {
     
                return match(s, p, sl, pl+2) || match(s, p, sl+1, pl);
            } else {
     
                return match(s, p, sl, pl+2);
            }
        }
    }

    bool isMatch(string s, string p) {
     
        return match(s, p, 0, 0);
    }
};

…

面试题 20. 表示数值的字符串

题目描述

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串"+100"、“5e2”、"-123"、“3.1416”、“0123"及”-1E-16"都表示数值，但"12e"、“1a3.14”、“1.2.3”、"±5"及"12e+5.4"都不是。

注意：本题与主站 65 题相同：https://leetcode-cn.com/problems/valid-number/

解法

遍历字符串：

出现 +/- 时，位置必须是在第 0 位，或者 e/E 的后面一位
出现 . 时，在此之前不能出现 . 或者 e/E
出现 e/E 时，前面不能出现 e/E，并且必须出现过数字

Python3

class Solution:
    def isNumber(self, s: str) -> bool:
        if not s or not s.strip():
            return False
        s = s.strip()
        find_num = find_dot = find_e = False
        for i in range(len(s)):
            if s[i] == '+' or s[i] == '-':
                if i != 0 and s[i - 1] != 'e' and s[i - 1] != 'E':
                    return False
            elif s[i] >= '0' and s[i] <= '9':
                find_num = True
            elif s[i] == '.':
                if find_dot or find_e:
                    return False
                find_dot = True
            elif s[i] == 'e' or s[i] == 'E':
                if not find_num or find_e:
                    return False
                find_e = True
                find_num = False
            else:
                return False
        return find_num

Java

class Solution {
     
    public boolean isNumber(String s) {
     
        if (s == null || s.trim().length() == 0) {
     
            return false;
        }
        char[] chars = s.trim().toCharArray();
        boolean findNum = false;
        boolean findE = false;
        boolean findDot = false;
        for (int i = 0, n = chars.length; i < n; ++i) {
     
            if (chars[i] == '+' || chars[i] == '-') {
     
                if (i != 0 && chars[i - 1] != 'e' && chars[i - 1] != 'E') {
     
                    return false;
                }
            } else if (chars[i] >= '0' && chars[i] <= '9') {
     
                findNum = true;
            } else if (chars[i] == '.') {
     
                if (findDot || findE) {
     
                    return false;
                }
                findDot = true;
            } else if (chars[i] == 'e' || chars[i] == 'E') {
     
                if (findE || !findNum) {
     
                    return false;
                }
                findE = true;
                findNum = false; // 确保e之后也出现数
            } else {
     
                return false;
            }
        }
        return findNum;
    }
}

JavaScript

/**
 * @param {string} s
 * @return {boolean}
 */
var isNumber = function (s) {
     
  return s !== " " && !isNaN(+s);
};

…

面试题 21. 调整数组顺序使奇数位于偶数前面

题目描述

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

示例：

输入：nums = [1,2,3,4]
输出：[1,3,2,4]
注：[3,1,2,4] 也是正确的答案之一。

提示：

1 <= nums.length <= 50000
1 <= nums[i] <= 10000

解法

双指针。

Python3

class Solution:
    def exchange(self, nums: List[int]) -> List[int]:
        p, q = 0, len(nums) - 1
        while p < q:
            if nums[p] & 1 == 1:
                p += 1
                continue
            if nums[q] & 1 == 0:
                q -= 1
                continue
            nums[p], nums[q] = nums[q], nums[p]
        return nums

Java

class Solution {
     
    public int[] exchange(int[] nums) {
     
        int p = 0, q = nums.length - 1;
        while (p < q) {
     
            if ((nums[p] & 1) == 1) {
     
                ++p;
                continue;
            }
            if ((nums[q] & 1) == 0) {
     
                --q;
                continue;
            }
            swap(nums, p, q);
        }
        return nums;
    }

    private void swap(int[] nums, int p, int q) {
     
        int t = nums[p];
        nums[p] = nums[q];
        nums[q] = t;
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @return {number[]}
 */
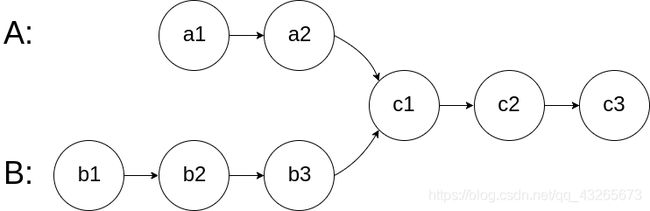
var exchange = function (nums) {
     
  let left = 0;
  let right = nums.length - 1;
  while (left < right) {
     
    let c = nums[left];
    nums[left] = nums[right];
    nums[right] = c;
    while (nums[left] % 2) {
     
      left++;
    }
    while (nums[right] % 2 === 0) {
     
      right--;
    }
  }
  return nums;
};

…

面试题 22. 链表中倒数第 k 个节点

题目描述

输入一个链表，输出该链表中倒数第 k 个节点。为了符合大多数人的习惯，本题从 1 开始计数，即链表的尾节点是倒数第 1 个节点。例如，一个链表有 6 个节点，从头节点开始，它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。

示例：

给定一个链表: 1->2->3->4->5, 和 k = 2.

返回链表 4->5.

解法

定义快慢指针 slow、fast，初始指向 head。

fast 先向前走 k 步，接着 slow、fast 同时向前走，当 fast 指向 null 时，slow 指向的节点即为链表的倒数第 k 个节点。

Python3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getKthFromEnd(self, head: ListNode, k: int) -> ListNode:
        slow = fast = head
        for _ in range(k):
            fast = fast.next
        while fast:
            slow = slow.next
            fast = fast.next
        return slow

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public ListNode getKthFromEnd(ListNode head, int k) {
     
        ListNode slow = head, fast = head;
        while (k-- > 0) {
     
            fast = fast.next;
        }
        while (fast != null) {
     
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }
}

JavaScript

/**
 * @param {ListNode} head
 * @param {number} k
 * @return {ListNode}
 */
var getKthFromEnd = function (head, k) {
     
  // 递归
  // let cnt = 1
  // function func(node) {
     
  //     if(!node || !node.next) return node
  //     let newNode = func(node.next)
  //     if(cnt === k) return newNode
  //     else cnt++
  //     return node
  // }
  // return func(head)

  // 快慢指针
  let slow = head;
  let fast = head;
  while (k) {
     
    fast = fast.next;
    k--;
  }
  while (fast) {
     
    slow = slow.next;
    fast = fast.next;
  }
  return slow;
};

Go

func getKthFromEnd(head *ListNode, k int) *ListNode {
     
    tmp := head
    for tmp != nil && k > 0{
     
        tmp = tmp.Next
        k--
    }
    slow := head
    fast := tmp
    for fast != nil {
     
        fast = fast.Next
        slow = slow.Next
    }
    return slow
}

…

面试题 24. 反转链表

题目描述

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

限制：

0 <= 节点个数 <= 5000

解法

定义指针 pre，cur 分别指向 null 和头节点。

遍历链表，将 cur.next 临时保存到 t 中，然后改变指针 cur 指向的节点的指向，将其指向 pre 指针指向的节点，即 cur.next = pre。然后 pre 指针指向 cur，cur 指针往前走。

当遍历结束后，返回 pre 指针即可。

Python3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        pre, cur = None, head
        while cur:
            t = cur.next
            cur.next = pre
            pre = cur
            cur = t
        return pre

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public ListNode reverseList(ListNode head) {
     
        ListNode pre = null, cur = head;
        while (cur != null) {
     
            ListNode t = cur.next;
            cur.next = pre;
            pre = cur;
            cur = t;
        }
        return pre;
    }
}

JavaScript

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function (head) {
     
  let node = head;
  let pre = null;
  while (node) {
     
    let cur = node;
    node = cur.next;
    cur.next = pre;
    pre = cur;
  }
  return pre;
};

Go

func reverseList(head *ListNode) *ListNode {
     
    if head == nil ||head.Next == nil {
     
        return head
    }
    dummyHead := &ListNode{
     }
    cur := head
    for cur != nil {
     
        tmp := cur.Next
        cur.Next = dummyHead.Next
        dummyHead.Next = cur
        cur = tmp
    }
    return dummyHead.Next
}

…

面试题 25. 合并两个排序的链表

题目描述

输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。

示例 1：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

限制：

0 <= 链表长度 <= 1000

解法

同时遍历两个链表，归并插入新链表中即可。

Python3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        dummy = ListNode(0)
        p = dummy
        while l1 and l2:
            if l1.val <= l2.val:
                p.next = l1
                l1 = l1.next
            else:
                p.next = l2
                l2 = l2.next
            p = p.next
        p.next = l1 or l2
        return dummy.next

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
     
        ListNode dummy = new ListNode(0);
        ListNode p = dummy;
        while (l1 != null && l2 != null) {
     
            if (l1.val <= l2.val) {
     
                p.next = l1;
                l1 = l1.next;
            } else {
     
                p.next = l2;
                l2 = l2.next;
            }
            p = p.next;
        }
        p.next = l1 == null ? l2 : l1;
        return dummy.next;
    }
}

JavaScript

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
var mergeTwoLists = function (l1, l2) {
     
  // 法一 - 递归
  if (!l1) return l2;
  if (!l2) return l1;
  if (l1.val < l2.val) {
     
    l1.next = mergeTwoLists(l1.next, l2);
    return l1;
  } else {
     
    l2.next = mergeTwoLists(l2.next, l1);
    return l2;
  }
  // 法二 - 遍历
  // if(!l1 || !l2) return l1 ? l1 : l2
  // let a = l1
  // let b = l2
  // let res = l1
  // if(a.val > b.val) {
     
  //     let c = a
  //     a = b
  //     b = c
  //     res = l2
  // }
  // while(a && b) {
     
  //     while(a.next && a.next.val < b.val) {
     
  //         a = a.next
  //     }
  //     let tmp = a.next
  //     let rec = b.next
  //     a.next = b
  //     a.next.next = tmp
  //     a = a.next
  //     b = rec
  // }
  // return res
};

Go

func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
     
    if l1 == nil {
     
        return l2
    }
    if l2 == nil {
     
        return l1
    }
    if l1.Val <= l2.Val {
     
        l1.Next = mergeTwoLists(l1.Next,l2)
        return l1
    }
    l2.Next = mergeTwoLists(l1, l2.Next)
    return l2
}

C++

class Solution {
     
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
     
        if (nullptr == l1 && nullptr == l2) {
     
            return nullptr;    // 两个都为空，则直接返回
        }

        if (nullptr == l1 || nullptr == l2) {
     
            return l1 == nullptr ? l2 : l1;    // 有且仅有一个为空，则返回非空节点
        }

        ListNode* node = nullptr;
        if (l1->val > l2->val) {
     
            node = l2;
            node->next = mergeTwoLists(l1, l2->next);
        } else {
     
            node = l1;
            node->next = mergeTwoLists(l1->next, l2);
        }

        return node;
    }
};

…

面试题 26. 树的子结构

题目描述

输入两棵二叉树 A 和 B，判断 B 是不是 A W 的子结构。(约定空树不是任意一个树的子结构)

B 是 A 的子结构，即 A 中有出现和 B 相同的结构和节点值。

例如:

给定的树 A:

给定的树 B：

   4 
  /
 1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

限制：

0 <= 节点个数 <= 10000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
        def sub(A, B):
            """判断从当前A节点开始，是否包含B"""
            if B is None:
                return True
            if A is None:
                return False
            return A.val == B.val and sub(A.left, B.left) and sub(A.right, B.right)
        if B is None or A is None:
            return False
        if A.val != B.val:
            return self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B)
        return sub(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public boolean isSubStructure(TreeNode A, TreeNode B) {
     
        if (B == null || A == null) return false;
        if (A.val != B.val) return isSubStructure(A.left, B) || isSubStructure(A.right, B);
        return sub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }

    private boolean sub(TreeNode A, TreeNode B) {
     
        // 判断从当前A节点开始，是否包含B
        if (B == null) return true;
        if (A == null) return false;
        return A.val == B.val && sub(A.left, B.left) && sub(A.right, B.right);
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} A
 * @param {TreeNode} B
 * @return {boolean}
 */
var isSubStructure = function (A, B) {
     
  function sub(A, B) {
     
    if (!B) return true;
    if (!A) return false;
    return A.val == B.val && sub(A.left, B.left) && sub(A.right, B.right);
  }
  if (!B || !A) return false;
  if (A.val != B.val)
    return isSubStructure(A.left, B) || isSubStructure(A.right, B);
  return sub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSubStructure(A *TreeNode, B *TreeNode) bool {
     
    // 约定空树不是任意一个树的子结构
    if A == nil || B == nil {
     
        return false
    }
    return helper(A,B) || isSubStructure(A.Left,B) || isSubStructure(A.Right,B)
}

func helper(a *TreeNode, b *TreeNode) bool {
     
    if b ==  nil {
     
        return true
    }
    if a == nil {
     
        return false
    }
    return a.Val == b.Val && helper(a.Left, b.Left) && helper(a.Right, b.Right)
}

C++

class Solution {
     
public:
    bool isSubTree(TreeNode* a, TreeNode* b) {
     
        if (nullptr == b) {
     
            // 如果小树走到头，则表示ok了
            return true;
        }

        if (nullptr == a) {
     
            // 如果大树走到头，小树却没走到头，说明不对了
            return false;
        }

        if (a->val != b->val) {
     
            return false;
        }

        return isSubTree(a->left, b->left) && isSubTree(a->right, b->right);
    }

    bool isSubStructure(TreeNode* a, TreeNode* b) {
     
        bool ret = false;
        if (nullptr != a && nullptr != b) {
     
            // 题目约定，空树不属于任何一个数的子树
            if (a->val == b->val) {
     
                // 如果值相等，才进入判定
                ret = isSubTree(a, b);
            }

            if (false == ret) {
     
                ret = isSubStructure(a->left, b);
            }

            if (false == ret) {
     
                ret = isSubStructure(a->right, b);
            }
        }

        return ret;
    }
};

…

面试题 27. 二叉树的镜像

题目描述

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

镜像输出：

     4
   /   \
  7     2
 / \   / \
9   6 3   1

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

限制：

0 <= 节点个数 <= 1000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        if root is None:
            return None
        root.left, root.right = root.right, root.left
        self.mirrorTree(root.left)
        self.mirrorTree(root.right)
        return root

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public TreeNode mirrorTree(TreeNode root) {
     
        if (root == null) return null;
        TreeNode t = root.left;
        root.left = root.right;
        root.right = t;
        mirrorTree(root.left);
        mirrorTree(root.right);
        return root;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var mirrorTree = function (root) {
     
  if (!root) return null;
  [root.left, root.right] = [root.right, root.left];
  mirrorTree(root.left);
  mirrorTree(root.right);
  return root;
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func mirrorTree(root *TreeNode) *TreeNode {
     
    if root == nil {
     
        return root
    }
    root.Left, root.Right = root.Right, root.Left
    mirrorTree(root.Left)
    mirrorTree(root.Right)
    return root
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
     
public:
    TreeNode* mirrorTree(TreeNode* root) {
     
        // 后续遍历
        if (nullptr == root) {
     
            return nullptr;
        }

        mirrorTree(root->left);
        mirrorTree(root->right);
        std::swap(root->left, root->right);

        return root;
    }
};

…

面试题 28. 对称的二叉树

题目描述

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

限制：

0 <= 节点个数 <= 1000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        def is_symmetric(left, right):
            if left is None and right is None:
                return True
            if left is None or right is None or left.val != right.val:
                return False
            return is_symmetric(left.left, right.right) and is_symmetric(left.right, right.left)
        if root is None:
            return True
        return is_symmetric(root.left, root.right)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public boolean isSymmetric(TreeNode root) {
     
        if (root == null) return true;
        return isSymmetric(root.left, root.right);
    }

    private boolean isSymmetric(TreeNode left, TreeNode right) {
     
        if (left == null && right == null) return true;
        if (left == null || right == null || left.val != right.val) return false;
        return isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isSymmetric = function (root) {
     
  function dfs(left, right) {
     
    if (!left && !right) return true;
    if (!left || !right || left.val != right.val) return false;
    return dfs(left.left, right.right) && dfs(left.right, right.left);
  }
  if (!root) return true;
  return dfs(root.left, root.right);
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSymmetric(root *TreeNode) bool {
     
    if root == nil {
     
        return true
    }
    return isSymme(root.Left, root.Right)
}

func isSymme(left *TreeNode, right *TreeNode) bool {
     
    if left == nil && right == nil {
     
        return true
    }
    if left == nil || right == nil || left.Val != right.Val {
     
        return false
    }
    return isSymme(left.Left, right.Right) && isSymme(left.Right, right.Left)
}

…

面试题 29. 顺时针打印矩阵

题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

限制：

0 <= matrix.length <= 100
0 <= matrix[i].length <= 100

解法

从外往里一圈一圈遍历并存储矩阵元素即可。

Python3

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        def add(i1, j1, i2, j2):
            if i1 == i2:
                return [matrix[i1][j] for j in range(j1, j2 + 1)]
            if j1 == j2:
                return [matrix[i][j1] for i in range(i1, i2 + 1)]
            return [matrix[i1][j] for j in range(j1, j2)] + [matrix[i][j2] for i in range(i1, i2)] + [matrix[i2][j] for j in range(j2, j1, -1)] + [matrix[i][j1] for i in range(i2, i1, -1)]
        if not matrix or not matrix[0]:
            return []
        m, n = len(matrix), len(matrix[0])
        i1, j1, i2, j2 = 0, 0, m - 1, n - 1
        res = []
        while i1 <= i2 and j1 <= j2:
            res += add(i1, j1, i2, j2)
            i1, j1, i2, j2 = i1 + 1, j1 + 1, i2 - 1, j2 - 1
        return res

Java

class Solution {
     
    private int[] res;
    private int index;

    public int[] spiralOrder(int[][] matrix) {
     
        int m, n;
        if (matrix == null || (m = matrix.length) == 0 || matrix[0] == null || (n = matrix[0].length) == 0)
            return new int[]{
     };
        res = new int[m * n];
        index = 0;
        int i1 = 0, i2 = m - 1;
        int j1 = 0, j2 = n - 1;
        while (i1 <= i2 && j1 <= j2) {
     
            add(matrix, i1++, j1++, i2--, j2--);
        }
        return res;
    }

    private void add(int[][] matrix, int i1, int j1, int i2, int j2) {
     
        if (i1 == i2) {
     
            for (int j = j1; j <= j2; ++j) {
     
                res[index++] = matrix[i1][j];
            }
            return;
        }
        if (j1 == j2) {
     
            for (int i = i1; i <= i2; ++i) {
     
                res[index++] = matrix[i][j1];
            }
            return;
        }
        for (int j = j1; j < j2; ++j) {
     
            res[index++] = matrix[i1][j];
        }
        for (int i = i1; i < i2; ++i) {
     
            res[index++] = matrix[i][j2];
        }
        for (int j = j2; j > j1; --j) {
     
            res[index++] = matrix[i2][j];
        }
        for (int i = i2; i > i1; --i) {
     
            res[index++] = matrix[i][j1];
        }
    }
}

JavaScript

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function (matrix) {
     
  if (!matrix || !matrix.length) return [];
  let row = matrix.length;
  let col = matrix[0].length;
  let res = [];
  let moves = {
     
    right: [0, 1],
    down: [1, 0],
    left: [0, -1],
    up: [-1, 0],
  };
  let k = 0;
  function dfs(i, j, dir) {
     
    if (i < 0 || j < 0 || i >= row || j >= col || res.length === row * col) {
     
      return;
    }
    res.push(matrix[i][j]);
    switch (dir) {
     
      case "right":
        if (j === col - 1 - k) dir = "down";
        break;
      case "down":
        if (i === row - 1 - k) dir = "left";
        break;
      case "left":
        if (j === k) {
     
          dir = "up";
          k++;
        }
        break;
      case "up":
        if (i === k) dir = "right";
        break;
    }
    let x = i + moves[dir][0];
    let y = j + moves[dir][1];
    dfs(x, y, dir);
  }
  dfs(0, 0, "right");
  return res;
};

…

面试题 30. 包含 min 函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.min();   --> 返回 -2.

提示：

各函数的调用总次数不超过 20000 次

解法

Python3

class MinStack:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.s1 = []
        self.s2 = []

    def push(self, x: int) -> None:
        self.s1.append(x)
        self.s2.append(x if not self.s2 or self.s2[-1] >= x else self.s2[-1])

    def pop(self) -> None:
        self.s1.pop()
        self.s2.pop()

    def top(self) -> int:
        return self.s1[-1]

    def min(self) -> int:
        return self.s2[-1]


# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.min()

Java

class MinStack {
     
    private Deque<Integer> s1;
    private Deque<Integer> s2;

    /** initialize your data structure here. */
    public MinStack() {
     
        s1 = new ArrayDeque<>();
        s2 = new ArrayDeque<>();
    }

    public void push(int x) {
     
        s1.push(x);
        s2.push(s2.isEmpty() || s2.peek() >= x ? x : s2.peek());
    }

    public void pop() {
     
        s1.pop();
        s2.pop();
    }

    public int top() {
     
        return s1.peek();
    }

    public int min() {
     
        return s2.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.min();
 */

JavaScript

/**
 * initialize your data structure here.
 */
var MinStack = function () {
     
  this.stack = [];
  this.minStack = [];
};

/**
 * @param {number} x
 * @return {void}
 */
MinStack.prototype.push = function (x) {
     
  this.stack.unshift(x);
  if (!this.minStack.length || this.minStack[0] >= x) {
     
    this.minStack.unshift(x);
  }
};

/**
 * @return {void}
 */
MinStack.prototype.pop = function () {
     
  if (this.stack.shift() === this.minStack[0]) {
     
    this.minStack.shift();
  }
};

/**
 * @return {number}
 */
MinStack.prototype.top = function () {
     
  return this.stack[0];
};

/**
 * @return {number}
 */
MinStack.prototype.min = function () {
     
  return this.minStack[0];
};

/**
 * Your MinStack object will be instantiated and called as such:
 * var obj = new MinStack()
 * obj.push(x)
 * obj.pop()
 * var param_3 = obj.top()
 * var param_4 = obj.min()
 */

…

面试题 31. 栈的压入、弹出序列

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

示例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

提示：

0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed 是 popped 的排列。

解法

借助一个辅助栈实现。

Python3

class Solution:
    def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
        s = []
        q = 0
        for num in pushed:
            s.append(num)
            while s and s[-1] == popped[q]:
                s.pop()
                q += 1
        return not s

Java

class Solution {
     
    public boolean validateStackSequences(int[] pushed, int[] popped) {
     
        Deque<Integer> s = new ArrayDeque<>();
        int q = 0;
        for (int num : pushed) {
     
            s.push(num);
            while (!s.isEmpty() && s.peek() == popped[q]) {
     
                s.pop();
                ++q;
            }
        }
        return s.isEmpty();
    }
}

JavaScript

/**
 * @param {number[]} pushed
 * @param {number[]} popped
 * @return {boolean}
 */
var validateStackSequences = function (pushed, popped) {
     
  let s = [];
  let q = 0;
  for (let num of pushed) {
     
    s.push(num);
    while (s.length > 0 && s[s.length - 1] == popped[q]) {
     
      ++q;
      s.pop();
    }
  }
  return s.length == 0;
};

…

面试题 32 - I. 从上到下打印二叉树

题目描述

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:

给定二叉树: [3,9,20,null,null,15,7],

返回：

[3,9,20,15,7]

提示：

节点总数 <= 1000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[int]:
        if root is None:
            return []
        q = deque()
        q.append(root)
        res = []
        while q:
            size = len(q)
            for _ in range(size):
                node = q.popleft()
                res.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
        return res

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public int[] levelOrder(TreeNode root) {
     
        if (root == null) return new int[]{
     };
        Deque<TreeNode> q = new ArrayDeque<>();
        List<Integer> t = new ArrayList<>();
        q.offer(root);
        while (!q.isEmpty()) {
     
            int size = q.size();
            while (size-- > 0) {
     
                TreeNode node = q.poll();
                t.add(node.val);
                if (node.left != null) q.offer(node.left);
                if (node.right != null) q.offer(node.right);
            }
        }
        int i = 0, n = t.size();
        int[] res = new int[n];
        for (Integer e : t) {
     
            res[i++] = e;
        }
        return res;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var levelOrder = function (root) {
     
  if (!root) return [];
  let queue = [root];
  let res = [];
  while (queue.length) {
     
    let node = queue.shift();
    if (!node) continue;
    res.push(node.val);
    queue.push(node.left, node.right);
  }
  return res;
};

Go

func levelOrder(root *TreeNode) []int {
     
    if root == nil {
     
        return []int{
     }
    }
    q := []*TreeNode{
     }
    q = append(q,root)
    //层序遍历,用队列,遍历到谁,就把谁的左右结点加入队列
    res := []int{
     }
    for len(q) != 0 {
     
        tmp := q[0]
        q = q[1:]
        res = append(res,tmp.Val)
        if tmp.Left != nil {
     
            q = append(q,tmp.Left)
        }
        if tmp.Right != nil {
     
            q = append(q,tmp.Right)
        }
    }
    return res
}

C++

class Solution {
     
public:
    vector<int> levelOrder(TreeNode* root) {
     
        vector<int> ret;
        if (!root) {
     
            return ret;
        }

        queue<TreeNode *> q;
        q.push(root);

        while (!q.empty()) {
     
            auto head = q.front();
            q.pop();
            ret.push_back(head->val);
            if (head->left) {
     
                q.push(head->left);
            }

            if (head->right) {
     
                q.push(head->right);
            }
        }

        return ret;
    }
};

…

面试题 32 - II. 从上到下打印二叉树 II

题目描述

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:

给定二叉树: [3,9,20,null,null,15,7],

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

提示：

节点总数 <= 1000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []
        q = deque()
        res = []
        q.append(root)
        while q:
            size = len(q)
            t = []
            for _ in range(size):
                node = q.popleft()
                t.append(node.val)
                if node.left is not None:
                    q.append(node.left)
                if node.right is not None:
                    q.append(node.right)
            res.append(t)
        return res

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public List<List<Integer>> levelOrder(TreeNode root) {
     
        if (root == null) return Collections.emptyList();
        Deque<TreeNode> q = new ArrayDeque<>();
        List<List<Integer>> res = new ArrayList<>();
        q.offer(root);
        while (!q.isEmpty()) {
     
            int size = q.size();
            List<Integer> t = new ArrayList<>();
            while (size-- > 0) {
     
                TreeNode node = q.poll();
                t.add(node.val);
                if (node.left != null) q.offer(node.left);
                if (node.right != null) q.offer(node.right);
            }
            res.add(t);
        }
        return res;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function (root) {
     
  if (!root) return [];
  let queue = [root];
  let res = [];
  let depth = 0;
  while (queue.length) {
     
    let len = queue.length;
    for (let i = 0; i < len; i++) {
     
      let node = queue.shift();
      if (!node) continue;
      if (!res[depth]) res[depth] = [];
      res[depth].push(node.val);
      queue.push(node.left, node.right);
    }
    depth++;
  }
  return res;
};

Go

func levelOrder(root *TreeNode) [][]int {
     
    if root == nil {
     
        return nil
    }
    res := [][]int{
     }
    queue := []*TreeNode{
     }
    queue = append(queue,root)
    for len(queue) != 0 {
     
        size := len(queue)
        ans := []int{
     }
        //利用一个变量记录每层大小
        for size > 0 {
     
            cur := queue[0]
            ans = append(ans, cur.Val)
            queue = queue[1:]
            size--
            if cur.Left != nil {
     
                queue = append(queue, cur.Left)
            }
            if cur.Right != nil {
     
                queue = append(queue, cur.Right)
            }
        }
        res = append(res, ans)
    }
    return res
}

…

面试题 32 - III. 从上到下打印二叉树 III

题目描述

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:

给定二叉树: [3,9,20,null,null,15,7],

返回其层次遍历结果：

[
  [3],
  [20,9],
  [15,7]
]

提示：

节点总数 <= 1000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []
        q = deque()
        res = []
        q.append(root)
        while q:
            size = len(q)
            t = []
            for _ in range(size):
                node = q.popleft()
                t.append(node.val)
                if node.left is not None:
                    q.append(node.left)
                if node.right is not None:
                    q.append(node.right)
            res.append(t if len(res) & 1 == 0 else t[::-1])
        return res

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public List<List<Integer>> levelOrder(TreeNode root) {
     
        if (root == null) return Collections.emptyList();
        Deque<TreeNode> q = new ArrayDeque<>();
        List<List<Integer>> res = new ArrayList<>();
        q.offer(root);
        while (!q.isEmpty()) {
     
            int size = q.size();
            List<Integer> t = new ArrayList<>();
            while (size-- > 0) {
     
                TreeNode node = q.poll();
                t.add(node.val);
                if (node.left != null) q.offer(node.left);
                if (node.right != null) q.offer(node.right);
            }
            if ((res.size() & 1) == 1) Collections.reverse(t);
            res.add(t);
        }
        return res;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function (root) {
     
  if (!root) return [];
  let queue = [root];
  let res = [];
  let depth = 0;
  let dir = true;
  while (queue.length) {
     
    let len = queue.length;
    for (let i = 0; i < len; i++) {
     
      let node = queue.shift();
      if (!node) continue;
      if (!res[depth]) res[depth] = [];
      if (dir) {
     
        res[depth].push(node.val);
      } else {
     
        res[depth].unshift(node.val);
      }
      queue.push(node.left, node.right);
    }
    depth++;
    dir = !dir;
  }
  return res;
};

Go

func levelOrder(root *TreeNode) [][]int {
     
    if root == nil {
     
        return nil
    }
    res := [][]int{
     }
    queue := []*TreeNode{
     }
    queue = append(queue,root)
    level := 0
    for len(queue) != 0 {
     
        size := len(queue)
        ans := []int{
     }
        //size记录每层大小,level记录层数
        for size > 0 {
     
            cur := queue[0]
            if level & 1 == 0 {
     
                ans = append(ans, cur.Val)
            } else {
     
                ans = append([]int{
     cur.Val},ans...)
            }

            queue = queue[1:]
            size--
            if cur.Left != nil {
     
                queue = append(queue, cur.Left)
            }
            if cur.Right != nil {
     
                queue = append(queue, cur.Right)
            }
        }
        level++
        res = append(res, ans)
    }
    return res
}

…

面试题 33. 二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这棵二叉搜索树：

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

提示：

数组长度 <= 1000

解法

二叉搜索树的后序遍历序列是 [左子树, 右子树, 根结点]，且左子树结点值均小于根结点，右子树结点值均大于根结点，递归判断即可。

Python3

class Solution:
    def verifyPostorder(self, postorder: List[int]) -> bool:
        def verify(p1, p2):
            if p1 > p2:
                return True
            pos = p1
            while pos < p2 and postorder[pos] < postorder[p2]:
                pos += 1
            p = pos
            while pos < p2:
                if postorder[pos] < postorder[p2]:
                    return False
                pos += 1
            return verify(p1, p - 1) and verify(p, p2 - 1)
        if not postorder:
            return True
        return verify(0, len(postorder) - 1)

Java

class Solution {
     
    public boolean verifyPostorder(int[] postorder) {
     
        int n;
        if (postorder == null || (n = postorder.length) == 0) return true;
        return verify(postorder, 0, n - 1);
    }

    private boolean  verify(int[] postorder, int p1, int p2) {
     
        if (p1 >= p2) return true;
        int pos = p1;
        while (pos < p2 && postorder[pos] < postorder[p2]) ++pos;
        int p = pos;
        while (pos < p2) {
     
            if (postorder[pos] < postorder[p2]) return false;
            ++pos;
        }
        return verify(postorder, p1, p - 1) && verify(postorder, p, p2 - 1);
    }
}

JavaScript

/**
 * @param {number[]} postorder
 * @return {boolean}
 */
var verifyPostorder = function (postorder) {
     
  if (!postorder || postorder.length < 2) return true;
  let mid = 0;
  let root = postorder[postorder.length - 1];
  for (let i = 0; i < postorder.length - 1 && postorder[i] < root; i++) {
     
    mid++;
  }
  for (let i = mid + 1; i < postorder.length - 1; i++) {
     
    if (postorder[i] < root) return false;
  }
  return (
    verifyPostorder(postorder.slice(0, mid)) &&
    verifyPostorder(postorder.slice(mid + 1, postorder.length - 1))
  );
};

Go

func verifyPostorder(postorder []int) bool {
     
    if len(postorder) < 2 {
     
        return true
    }
    return helper(postorder, 0, len(postorder)-1)
}
// 递归
func helper(postorder []int , left,right int) bool {
     
    if left >= right {
     
        return true
    }
    // 最后一位即根
    rootValue := postorder[right]
    // 从左开始往右遍历，直到大于根停止,小于部分是左子树
    i := left
    for i < right && postorder[i] < rootValue {
     
        i++
    }
    // 剩下部分是右子树，检查是否都大于根值
    for j := i; j < right; j++ {
     
        if postorder[j] < rootValue {
     
            return false
        }
    }
    l := helper(postorder,left,i-1) // 检查左子树，左子树i要减一
    r := helper(postorder,i,right-1)// 检查右子树，剔除最后一位是根
    return l && r
}

…

面试题 34. 二叉树中和为某一值的路径

题目描述

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:

给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1

[
   [5,4,11,2],
   [5,8,4,5]
]

提示：

节点总数 <= 10000

解法

先序遍历+路径记录。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
        def dfs(root, sum):
            if root is None:
                return
            path.append(root.val)
            if root.val == sum and root.left is None and root.right is None:
                res.append(path.copy())
            dfs(root.left, sum - root.val)
            dfs(root.right, sum - root.val)
            path.pop()
        if not root:
            return []
        res = []
        path = []
        dfs(root, sum)
        return res

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    private List<List<Integer>> res;
    private List<Integer> path;

    public List<List<Integer>> pathSum(TreeNode root, int sum) {
     
        if (root == null) return Collections.emptyList();
        res = new ArrayList<>();
        path = new ArrayList<>();
        dfs(root, sum);
        return res;
    }

    private void dfs(TreeNode root, int sum) {
     
        if (root == null) {
     
            return;
        }
        path.add(root.val);
        if (root.val == sum && root.left == null && root.right == null) {
     
            res.add(new ArrayList<>(path));
        }
        dfs(root.left, sum - root.val);
        dfs(root.right, sum - root.val);
        path.remove(path.size() - 1);
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} sum
 * @return {number[][]}
 */
var pathSum = function (root, sum) {
     
  if (!root) return [];
  let res = [];
  function dfs(node, sum, arr) {
     
    if (!node) return;
    arr = [...arr, node.val];
    if (node.val === sum && !node.left && !node.right) {
     
      res.push(arr);
      return;
    }
    dfs(node.left, sum - node.val, arr);
    dfs(node.right, sum - node.val, arr);
  }
  dfs(root, sum, []);
  return res;
};

Go

var res [][]int
func pathSum(root *TreeNode, sum int) [][]int {
     
    res = [][]int{
     }
    if root == nil {
     
        return res
    }
    helper(root, sum, []int{
     })
    return res
}

func helper(node *TreeNode, target int, ans []int) {
     
    if node == nil {
     
        return
    }
    ans = append(ans,node.Val)
    target -= node.Val
    if target == 0 && node.Left == nil && node.Right == nil {
     
        tmp := make([]int,len(ans))
        copy(tmp,ans)
        res = append(res,tmp)
    } else {
     
        helper(node.Left, target, ans)
        helper(node.Right, target, ans)
    }
}

…

面试题 35. 复杂链表的复制

题目描述

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

示例 1：

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

示例 4：

输入：head = []
输出：[]
解释：给定的链表为空（空指针），因此返回 null。

提示：

-10000 <= Node.val <= 10000
Node.random 为空（null）或指向链表中的节点。
节点数目不超过 1000 。

解法

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
        self.val = int(x)
        self.next = next
        self.random = random
"""
class Solution:
    def copyRandomList(self, head: 'Node') -> 'Node':
        if not head:
            return None
        copy_head = Node(-1)
        cur, t = copy_head, head
        cache = {
     }
        while t:
            cur.next = Node(t.val)
            cache[t] = cur.next
            cur, t = cur.next, t.next
        t, cur = head, copy_head.next
        while t:
            cur.random = cache.get(t.random)
            cur, t = cur.next, t.next
        return copy_head.next

Java

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/
class Solution {
     
    public Node copyRandomList(Node head) {
     
        if (head == null) {
     
            return null;
        }
        Map<Node, Node> map = new HashMap<>();
        Node copyHead = new Node(-1);
        Node cur = copyHead, t = head;
        while (t != null) {
     
            Node node = new Node(t.val);
            map.put(t, node);
            cur.next = node;
            cur = node;
            t = t.next;
        }
        cur = copyHead.next;
        while (head != null) {
     
            cur.random = map.get(head.random);
            cur = cur.next;
            head = head.next;
        }
        return copyHead.next;

    }
}

JavaScript

/**
 * // Definition for a Node.
 * function Node(val, next, random) {
 *    this.val = val;
 *    this.next = next;
 *    this.random = random;
 * };
 */
/**
 * @param {Node} head
 * @return {Node}
 */
var copyRandomList = function (head) {
     
  function copy(node) {
     
    if (!node) return null;
    if (isRead.get(node)) return isRead.get(node);
    let newNode = new Node(node.val);
    isRead.set(node, newNode);
    newNode.random = copy(node.random);
    newNode.next = copy(node.next);
    return newNode;
  }
  let isRead = new Map();
  return copy(head);
};

Go

func copyRandomList(head *Node) *Node {
     
    if head == nil {
     
        return nil
    }
    cur, next := head,head
    //完成对当前节点的复制
    for cur != nil {
     
        next = cur.Next
        cur.Next = &Node{
     
            Val: cur.Val,
            Next: next,
            Random: nil,
        }
        cur = next
    }
    //设置复制节点的random节点
    cur = head
    curCopy := head
    for cur != nil {
     
        next = cur.Next.Next
        curCopy = cur.Next
        if cur.Random == nil {
     
            curCopy.Random = nil
        } else {
     
            curCopy.Random = cur.Random.Next
        }
        cur = next
    }
    res := head.Next
    cur = head
    for cur != nil {
     
        next = cur.Next.Next
        curCopy = cur.Next
        cur.Next = next
        if next != nil {
     
            curCopy.Next = next.Next
        } else {
     
            curCopy.Next = nil
        }
        cur = cur.Next
    }
    return res
}

…

面试题 36. 二叉搜索树与双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

注意：本题与主站 426 题相同：https://leetcode-cn.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list/

注意：此题对比原题有改动。

解法

排序链表：二叉搜索树中序遍历得到有序序列
循环链表：头节点指向链表尾节点，尾节点指向链表头节点
双向链表：pre.right = cur、cur.left = pre、pre = cur

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
"""
class Solution:
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        def dfs(cur):
            if cur is None:
                return
            dfs(cur.left)
            if self.pre is None:
                self.head = cur
            else:
                self.pre.right = cur
            cur.left = self.pre
            self.pre = cur
            dfs(cur.right)
        if root is None:
            return None
        self.head = self.pre = None
        dfs(root)
        self.head.left = self.pre
        self.pre.right = self.head
        return self.head

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
     
    Node head;
    Node pre;
    public Node treeToDoublyList(Node root) {
     
        if (root == null) return null;
        dfs(root);
        head.left = pre;
        pre.right = head;
        return head;
    }

    private void dfs(Node cur) {
     
        if (cur == null) return;
        dfs(cur.left);
        if (pre == null) head = cur;
        else pre.right = cur;
        cur.left = pre;
        pre = cur;
        dfs(cur.right);
    }
}

JavaScript

/**
 * // Definition for a Node.
 * function Node(val,left,right) {
 *    this.val = val;
 *    this.left = left;
 *    this.right = right;
 * };
 */
/**
 * @param {Node} root
 * @return {Node}
 */
var treeToDoublyList = function (root) {
     
  function dfs(cur) {
     
    if (!cur) return;
    dfs(cur.left);
    if (!pre) head = cur;
    else pre.right = cur;
    cur.left = pre;
    pre = cur;
    dfs(cur.right);
  }
  if (!root) return null;
  let head, pre;
  dfs(root);
  head.left = pre;
  pre.right = head;
  return head;
};

…

面试题 37. 序列化二叉树

题目描述

请实现两个函数，分别用来序列化和反序列化二叉树。

示例:

你可以将以下二叉树：

    1
   / \
  2   3
     / \
    4   5

序列化为 "[1,2,3,null,null,4,5]"

注意：本题与主站 297 题相同：https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/

解法

层次遍历解决。

Python3

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.

        :type root: TreeNode
        :rtype: str
        """
        if not root:
            return '[]'
        queue = collections.deque()
        queue.append(root)
        res = []
        while queue:
            node = queue.popleft()
            if node:
                res.append(str(node.val))
                queue.append(node.left)
                queue.append(node.right)
            else:
                res.append('null')
        return f'[{",".join(res)}]'


    def deserialize(self, data):
        """Decodes your encoded data to tree.

        :type data: str
        :rtype: TreeNode
        """
        if not data or data == '[]':
            return None
        queue = collections.deque()
        nodes = data[1:-1].split(',')
        root = TreeNode(nodes[0])
        queue.append(root)
        idx = 1
        while queue and idx < len(nodes):
            node = queue.popleft()
            if nodes[idx] != 'null':
                node.left = TreeNode(nodes[idx])
                queue.append(node.left)
            idx += 1
            if nodes[idx] != 'null':
                node.right = TreeNode(nodes[idx])
                queue.append(node.right)
            idx += 1
        return root


# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.deserialize(codec.serialize(root))

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {
     

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
     
        if (root == null) {
     
            return "[]";
        }
        StringBuilder sb = new StringBuilder("[");
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
     
            TreeNode node = queue.poll();
            if (node != null) {
     
                sb.append(node.val);
                queue.offer(node.left);
                queue.offer(node.right);
            } else {
     
                sb.append("null");
            }
            sb.append(",");
        }
        return sb.deleteCharAt(sb.length() - 1).append("]").toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
     
        if (data == null || "[]".equals(data)) {
     
            return null;
        }
        String[] nodes = data.substring(1, data.length() - 1).split(",");
        Queue<TreeNode> queue = new LinkedList<>();
        TreeNode root = new TreeNode(Integer.parseInt(nodes[0]));
        queue.offer(root);
        int idx = 1;
        while (!queue.isEmpty() && idx < nodes.length) {
     
            TreeNode node = queue.poll();
            if (!"null".equals(nodes[idx])) {
     
                node.left = new TreeNode(Integer.parseInt(nodes[idx]));
                queue.offer(node.left);
            }
            ++idx;
            if (!"null".equals(nodes[idx])) {
     
                node.right = new TreeNode(Integer.parseInt(nodes[idx]));
                queue.offer(node.right);
            }
            ++idx;
        }
        return root;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * Encodes a tree to a single string.
 *
 * @param {TreeNode} root
 * @return {string}
 */
var serialize = function (root) {
     
  if (!root) return "[]";
  let queue = [root];
  let res = "";
  while (queue.length) {
     
    let node = queue.shift();
    if (node) {
     
      res += node.val + ",";
      queue.push(node.left);
      queue.push(node.right);
    } else {
     
      res += "null" + ",";
    }
  }
  return `[${
       res.substring(0, res.length - 1)}]`;
};

/**
 * Decodes your encoded data to tree.
 *
 * @param {string} data
 * @return {TreeNode}
 */
var deserialize = function (data) {
     
  if (!data || data.length <= 2) return null;
  let arr = data.substring(1, data.length - 1).split(",");
  let root = new TreeNode(arr.shift());
  let queue = [root];
  while (queue.length) {
     
    let node = queue.shift();
    let leftVal = arr.shift();
    if (leftVal !== "null") {
     
      node.left = new TreeNode(leftVal);
      queue.push(node.left);
    }
    let rightVal = arr.shift();
    if (rightVal !== "null") {
     
      node.right = new TreeNode(rightVal);
      queue.push(node.right);
    }
  }
  return root;
};

/**
 * Your functions will be called as such:
 * deserialize(serialize(root));
 */

…

面试题 38. 字符串的排列

题目描述

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

限制：

1 <= s 的长度 <= 8

解法

Python3

class Solution:
    def permutation(self, s: str) -> List[str]:
        def dfs(x):
            if x == len(s) - 1:
                res.append("".join(chars))
                return
            t = set()
            for i in range(x, len(s)):
                if chars[i] in t:
                    continue
                t.add(chars[i])
                chars[i], chars[x] = chars[x], chars[i]
                dfs(x + 1)
                chars[i], chars[x] = chars[x], chars[i]
        chars, res = list(s), []
        dfs(0)
        return res

Java

class Solution {
     
    private char[] chars;
    private List<String> res;

    public String[] permutation(String s) {
     
        chars = s.toCharArray();
        res = new ArrayList<>();
        dfs(0);
        return res.toArray(new String[res.size()]);
    }

    private void dfs(int x) {
     
        if (x == chars.length - 1) {
     
            res.add(String.valueOf(chars));
            return;
        }
        Set<Character> set = new HashSet<>();
        for (int i = x; i < chars.length; ++i) {
     
            if (set.contains(chars[i])) {
     
                continue;
            }
            set.add(chars[i]);
            swap(i, x);
            dfs(x + 1);
            swap(i, x);
        }
    }

    private void swap(int i, int j) {
     
        char t = chars[i];
        chars[i] = chars[j];
        chars[j] = t;
    }
}

JavaScript

/**
 * @param {string} s
 * @return {string[]}
 */
var permutation = function (s) {
     
  let len = s.length;
  let res = new Set();
  function dfs(str, isRead) {
     
    if (str.length === len) {
     
      res.add(str);
      return;
    }
    for (let i = 0; i < len; i++) {
     
      if (isRead[i]) continue;
      isRead[i] = 1;
      dfs(str.concat(s[i]), isRead);
      isRead[i] = 0;
    }
  }
  dfs("", {
     });
  return [...res];
};

C++

class Solution {
     
public:
    void func(string str, int index, set<string>& mySet) {
     
        if (index == str.size()) {
     
            // 当轮训到最后一个字符的时候，直接放入set中。加入set结构，是为了避免插入的值重复
            mySet.insert(str);
        } else {
     
            for (int i = index; i < str.size(); i++) {
     
                // 从传入位置(index)开始算，固定第一个字符，然后后面的字符依次跟index位置交换
                swap(str[i], str[index]);
                int temp = index + 1;
                func(str, temp, mySet);
                swap(str[i], str[index]);
            }
        }
    }

    vector<string> permutation(string s) {
     
        set<string> mySet;
        func(s, 0, mySet);
        vector<string> ret;
        for (auto& x : mySet) {
     
            /* 这一题加入mySet是为了进行结果的去重。
               但由于在最后加入了将set转vector的过程，所以时间复杂度稍高 */
            ret.push_back(x);
        }
        return ret;
    }
};

…

面试题 39. 数组中出现次数超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1:

输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2

限制：

1 <= 数组长度 <= 50000

解法

摩尔投票法。时间复杂度 O(n)，空间复杂度 O(1)。

Python3

class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        cnt = major = 0
        for num in nums:
            if cnt == 0:
                major = num
                cnt += 1
            else:
                cnt += (1 if major == num else -1)
        return major

Java

class Solution {
     
    public int majorityElement(int[] nums) {
     
        int major = 0, cnt = 0;
        for (int num : nums) {
     
            if (cnt == 0) {
     
                major = num;
                ++cnt;
            } else {
     
                cnt += (num == major ? 1 : -1);
            }
        }
        return major;
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @return {number}
 */
var majorityElement = function (nums) {
     
  let cnt = 0;
  let mode = -1;
  for (let num of nums) {
     
    if (!cnt) {
     
      mode = num;
      cnt++;
    } else {
     
      if (mode === num) cnt++;
      else cnt--;
    }
  }
  return mode;
  // return nums.sort((a,b)=>a-b)[~~(nums.length/2)]
};

…

面试题 40. 最小的 k 个数

题目描述

输入整数数组 arr，找出其中最小的 k 个数。例如，输入 4、5、1、6、2、7、3、8 这 8 个数字，则最小的 4 个数字是 1、2、3、4。

示例 1：

输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：

输入：arr = [0,1,2,1], k = 1
输出：[0]

限制：

0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000

解法

Python3

import heapq

class Solution:
    def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
        if k == 0:
            return []
        heap = []
        for e in arr:
            heapq.heappush(heap, e)
        return heapq.nsmallest(k, heap)

Java

class Solution {
     
    public int[] getLeastNumbers(int[] arr, int k) {
     
        if (k == 0) {
     
            return new int[]{
     };
        }
        PriorityQueue<Integer> bigRoot = new PriorityQueue<>(k, Collections.reverseOrder());
        for (int e : arr) {
     
            if (bigRoot.size() < k) {
     
                bigRoot.offer(e);
            } else if (e < bigRoot.peek()) {
     
                bigRoot.poll();
                bigRoot.offer(e);
            }
        }
        int[] res = new int[k];
        for (int i = 0; i < k; ++i) {
     
            res[i] = bigRoot.poll();
        }
        return res;
    }
}

JavaScript

/**
 * @param {number[]} arr
 * @param {number} k
 * @return {number[]}
 */
var getLeastNumbers = function (arr, k) {
     
  // 排序
  // return arr.sort((a,b)=>a-b).slice(0,k)
  // ==========================================
  // 快排思想
  let left = 0;
  let right = arr.length - 1;
  while (left < right) {
     
    let i = partition(left, right);
    if (i <= k) {
     
      left = i + 1;
    }
    if (i >= k) {
     
      right = i - 1;
    }
  }
  function partition(left, right) {
     
    let pivot = arr[left];
    while (left < right) {
     
      while (left < right && arr[right] >= pivot) {
     
        right--;
      }
      arr[left] = arr[right];
      while (left < right && arr[left] <= pivot) {
     
        left++;
      }
      arr[right] = arr[left];
    }
    arr[left] = pivot;
    return left;
  }
  return arr.slice(0, k);
};

C++

class Solution {
     
public:
    int partition(vector<int>& arr, int begin, int end) {
     
        int l = begin;
        int r = end;
        int povit = arr[begin];

        while (l < r) {
     
            // 从右边开始，找到第一个小于povit的数字（用于交换）
            while (l < r && arr[r] >= povit) {
      r--; }
            while (l < r && arr[l] <= povit) {
      l++; }
            if (l < r) {
      swap(arr[l], arr[r]); }
        }

        swap(arr[begin], arr[l]);
        return l;
    }

    void partSort(vector<int>& arr, int begin, int end, int target) {
     
        if (begin >= end) {
     
            return;
        }

        // 思路类似快排，这样做比堆排序时间复杂度低
        // C++中，stl提供partial_sort()方法，就是这种实现方式
        int mid = partition(arr, begin, end);
        if (mid == target) {
     
            return;
        } else if (target < mid) {
     
            partSort(arr, begin, mid - 1, target);
        } else {
     
            partSort(arr, mid + 1, end, target);
        }

        return;
    }

    vector<int> getLeastNumbers(vector<int>& arr, int k) {
     
        partSort(arr, 0, arr.size() - 1, k - 1);
        vector<int> ret(arr.begin(), arr.begin() + k);
        return ret;
    }
};

…

面试题 41. 数据流中的中位数

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

示例 1：

输入：
["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"]
[[],[1],[2],[],[3],[]]
输出：[null,null,null,1.50000,null,2.00000]

示例 2：

输入：
["MedianFinder","addNum","findMedian","addNum","findMedian"]
[[],[2],[],[3],[]]
输出：[null,null,2.00000,null,2.50000]

限制：

最多会对 addNum、findMedia 进行 50000 次调用。

注意：本题与主站 295 题相同：https://leetcode-cn.com/problems/find-median-from-data-stream/

解法

创建大根堆、小根堆，其中：大根堆存放较小的一半元素，小根堆存放较大的一半元素。
添加元素时，若两堆元素个数相等，放入小根堆（使得小根堆个数多 1）；若不等，放入大根堆（使得大小根堆元素个数相等）
取中位数时，若两堆元素个数相等，取两堆顶求平均值；若不等，取小根堆堆顶。

Python3

class MedianFinder:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.max_heap = []
        self.min_heap = []


    def addNum(self, num: int) -> None:
        if len(self.max_heap) == len(self.min_heap):
            heapq.heappush(self.min_heap, -heapq.heappushpop(self.max_heap, -num))
        else:
            heapq.heappush(self.max_heap, -heapq.heappushpop(self.min_heap, num))

    def findMedian(self) -> float:
        return (-self.max_heap[0] + self.min_heap[0]) / 2 if len(self.max_heap) == len(self.min_heap) else self.min_heap[0]


# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()

Java

class MedianFinder {
     
    Queue<Integer> minHeap;
    Queue<Integer> maxHeap;

    /** initialize your data structure here. */
    public MedianFinder() {
     
        minHeap = new PriorityQueue<>();
        maxHeap = new PriorityQueue<>((a, b) -> b - a);
    }

    public void addNum(int num) {
     
        if (maxHeap.size() == minHeap.size()) {
     
            maxHeap.offer(num);
            // 放入小根堆(小根堆多1)
            minHeap.offer(maxHeap.poll());
        } else {
     
            minHeap.offer(num);
            // 放入大根堆(大小堆数量相等)
            maxHeap.offer(minHeap.poll());
        }
    }

    public double findMedian() {
     
        if (((maxHeap.size() + minHeap.size()) & 1) == 0) {
     
            // 偶数个，取两个堆顶平均值
            return (maxHeap.peek() + minHeap.peek()) / 2.0;
        }
        return minHeap.peek();
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

JavaScript

/**
 * initialize your data structure here.
 */
var MedianFinder = function () {
     
  this.val = [];
};

/**
 * @param {number} num
 * @return {void}
 */
MedianFinder.prototype.addNum = function (num) {
     
  let left = 0;
  let right = this.val.length;
  while (left < right) {
     
    let mid = left + ~~((right - left) / 2);
    if (num > this.val[mid]) {
     
      left = mid + 1;
    } else {
     
      right = mid;
    }
  }
  this.val.splice(left, 0, num);
};

/**
 * @return {number}
 */
MedianFinder.prototype.findMedian = function () {
     
  let mid = ~~(this.val.length / 2);
  return this.val.length % 2
    ? this.val[mid]
    : (this.val[mid - 1] + this.val[mid]) / 2;
};

…

面试题 42. 连续子数组的最大和

题目描述

输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为 O(n)。

示例 1:

输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

提示：

1 <= arr.length <= 10^5
-100 <= arr[i] <= 100

注意：本题与主站 53 题相同：https://leetcode-cn.com/problems/maximum-subarray/

解法

设 dp[i] 表示 [0..i] 中，以 nums[i] 结尾的最大子数组和，状态转移方程 dp[i] = nums[i] + max(dp[i - 1], 0)。

由于 dp[i] 只与子问题 dp[i-1] 有关，故可以用一个变量 f 来表示。

Python3

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        n = len(nums)
        res = f = nums[0]
        for i in range(1, n):
            f = nums[i] + max(f, 0)
            res = max(res, f)
        return res

Java

class Solution {
     
    public int maxSubArray(int[] nums) {
     
        int res = nums[0], f = nums[0];
        for (int i = 1, n = nums.length; i < n; ++i) {
     
            f = nums[i] + Math.max(f, 0);
            res = Math.max(res, f);
        }
        return res;
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @return {number}
 */
var maxSubArray = function (nums) {
     
  if (!nums || !nums.length) return null;
  let len = nums.length;
  let dp = new Array(len);
  dp[0] = nums[0];
  for (let i = 1; i < len; i++) {
     
    dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
  }
  return Math.max(...dp);
};

…

面试题 43. 1 ～ n 整数中 1 出现的次数

题目描述

输入一个整数 n ，求 1 ～ n 这 n 个整数的十进制表示中 1 出现的次数。

例如，输入 12，1 ～ 12 这些整数中包含 1 的数字有 1、10、11 和 12，1 一共出现了 5 次。

示例 1：

输入：n = 12
输出：5

示例 2：

输入：n = 13
输出：6

限制：

1 <= n < 2^31

注意：本题与主站 233 题相同：https://leetcode-cn.com/problems/number-of-digit-one/

解法

将 n 拆为两部分：最高位 high 和低位 lows。按 high 是否为 1 分别递归求解结果 f(n)。

以 n=3356 举例说明。

high=3,lows=356,base=1000。此时 n 可拆分为 0~999,1000~1999,2000~2999,3000~3356，其中：

0~999 范围内 1 的个数为 f(base-1)
1000~1999 范围内 1 的个数可分为两部分：千位、其余位。千位都为 1，所以 1 的个数为 base+f(base-1)
2000~2999 范围内 1 的个数为 f(base-1)
3000~3356 范围内 1 的个数为 f(lows)

因此，1 的总个数为 high*f(base-1)+f(lows)+base。

最高位非 1 的情况，也可以按照同样的方法分析。

Python3

from functools import lru_cache

class Solution:
    @lru_cache
    def countDigitOne(self, n: int) -> int:
        if n < 1:
            return 0
        s = str(n)
        high = int(s[0])
        base = pow(10, len(s) - 1)
        lows = n % base
        return self.countDigitOne(base - 1) + lows + 1 + self.countDigitOne(lows) if high == 1 else high * self.countDigitOne(base - 1) + base + self.countDigitOne(lows)

Java

class Solution {
     
    public int countDigitOne(int n) {
     
        if (n < 1) {
     
            return 0;
        }
        String s = String.valueOf(n);
        int high = s.charAt(0) - '0'; // 最高位
        int base = (int) Math.pow(10, s.length() - 1); // 基数
        int lows = n % base; // 低位
        return high == 1
            ? countDigitOne(base - 1) + countDigitOne(lows) + lows + 1
            : high * countDigitOne(base - 1) + countDigitOne(lows) + base;
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var countDigitOne = function (n) {
     
  let res = 0;
  let i = 1;
  while (i <= n) {
     
    let high = ~~(n / i / 10);
    let cur = ~~(n / i) % 10;
    let low = n - ~~(n / i) * i;
    switch (cur) {
     
      case 0:
        res += high * i;
        break;
      case 1:
        res += high * i + low + 1;
        break;
      default:
        res += (high + 1) * i;
    }
    i *= 10;
  }
  return res;
};

…

面试题 44. 数字序列中某一位的数字

题目描述

数字以 0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中，第 5 位（从下标 0 开始计数）是 5，第 13 位是 1，第 19 位是 4，等等。

请写一个函数，求任意第 n 位对应的数字。

示例 1：

输入：n = 3
输出：3

示例 2：

输入：n = 11
输出：0

限制：

0 <= n < 2^31

注意：本题与主站 400 题相同：https://leetcode-cn.com/problems/nth-digit/

解法

pow = 0：0~9 有 10 位
pow = 1: 10~99 有 90*2=180 位
pow = 2: 100~999 有 900*3=2700 位。

先求出第 n 位所在的 pow 和真实数字，进而求出真实数字的第 n % (pow + 1) 位即可。

Python3

class Solution:
    def findNthDigit(self, n: int) -> int:
        def get_bit_num():
            return 10 if p == 0 else 9 * pow(10, p) * (p + 1)

        if n < 10:
            return n
        p = count = 0
        while 1:
            count = get_bit_num()
            if n < count: break
            n -= count
            p += 1
        num = n // (p + 1) + pow(10, p)
        return int(str(num)[n % (p + 1)])

Java

class Solution {
     
    public int findNthDigit(int n) {
     
        if (n < 10) return n;
        int pow = 0, count;
        while (true) {
     
            count = getBitNum(pow);
            if (n < count) break;
            n -= count;
            ++pow;
        }
        int num = n / (pow + 1) + (int) Math.pow(10, pow);
        return String.valueOf(num).charAt(n % (pow + 1)) - '0';
    }

    private int getBitNum(int pow) {
     
        if (pow == 0) {
     
            return 10;
        }
        return (int) (9 * Math.pow(10, pow) * (pow + 1));
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var findNthDigit = function (n) {
     
  let i = 9;
  let a = 1;
  let remain = n;
  while (i * a < remain) {
     
    remain -= i * a;
    i *= 10;
    a++;
  }
  let b = remain % a;
  let res = 10 ** (a - 1) + ~~(remain / a);
  if (b === 0) {
     
    b = a;
    res--;
  }
  return res.toString()[b - 1];
};

…

面试题 45. 把数组排成最小的数

题目描述

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。

示例 1:

输入: [10,2]
输出: "102"

示例 2:

输入: [3,30,34,5,9]
输出: "3033459"

提示:

0 < nums.length <= 100

说明:

输出结果可能非常大，所以你需要返回一个字符串而不是整数。
拼接起来的数字可能会有前导 0，最后结果不需要去掉前导 0。

解法

自定义排序比较器。

Python3

import functools

class Solution:
    def minNumber(self, nums: List[int]) -> str:
        if not nums:
            return ''

        def compare(s1, s2):
            if s1 + s2 < s2 + s1:
                return -1
            if s1 + s2 > s2 + s1:
                return 1
            return 0

        return ''.join(sorted([str(x) for x in nums], key=functools.cmp_to_key(compare)))

Java

class Solution {
     
    public String minNumber(int[] nums) {
     
        if (nums == null || nums.length == 0) {
     
            return "";
        }
        return Arrays.stream(nums).mapToObj(String::valueOf).sorted((s1, s2) -> (s1 + s2).compareTo(s2 + s1)).reduce((s1, s2) -> s1 + s2).get();
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @return {string}
 */
var minNumber = function (nums) {
     
  nums.sort((a, b) => {
     
    let s1 = a + "" + b;
    let s2 = b + "" + a;
    if (s1 < s2) {
     
      return -1;
    } else return 1;
  });
  return nums.join("");
};

…

面试题 46. 把数字翻译成字符串

题目描述

给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

示例 1:

输入: 12258
输出: 5
解释: 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"

提示：

0 <= num < 2³¹

解法

递归求解。

Python3

class Solution:
    def translateNum(self, num: int) -> int:
        def cal(s):
            if len(s) < 2:
                return 1
            t = int(s[:2])
            return cal(s[1:]) if t < 10 or t > 25 else cal(s[1:]) + cal(s[2:])
        return cal(str(num))

Java

class Solution {
     
    public int translateNum(int num) {
     
        return cal(String.valueOf(num));
    }

    private int cal(String s) {
     
        int n = s.length();
        if (n < 2) {
     
            return 1;
        }
        int t = Integer.parseInt(s.substring(0, 2));
        return t < 10 || t > 25 ? cal(s.substring(1)) : cal(s.substring(1)) + cal(s.substring(2));
    }
}

JavaScript

/**
 * @param {number} num
 * @return {number}
 */
var translateNum = function (num) {
     
  let res = 0;
  num = num.toString();
  function dfs(i) {
     
    if (i >= num.length) {
     
      res++;
      return;
    }
    dfs(i + 1);
    let tmp = +(num[i] + num[i + 1]);
    if (num[i] !== "0" && tmp >= 0 && tmp < 26) {
     
      dfs(i + 2);
    }
  }
  dfs(0);
  return res;
};

…

面试题 47. 礼物的最大价值

题目描述

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例 1:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

提示：

0 < grid.length <= 200
0 < grid[0].length <= 200

解法

Python3

class Solution:
    def maxValue(self, grid: List[List[int]]) -> int:
        rows, cols = len(grid), len(grid[0])
        vals = [[0 for _ in range(cols)] for _ in range(rows)]
        vals[0][0] = grid[0][0]
        for i in range(1, rows):
            vals[i][0] = vals[i - 1][0] + grid[i][0]
        for j in range(1, cols):
            vals[0][j] = vals[0][j - 1] + grid[0][j]
        for i in range(1, rows):
            for j in range(1, cols):
                vals[i][j] = grid[i][j] + max(vals[i - 1][j], vals[i][j - 1])
        return vals[rows - 1][cols - 1]

Java

class Solution {
     
    public int maxValue(int[][] grid) {
     
        int rows = grid.length, cols = grid[0].length;
        int[][] vals = new int[rows][cols];
        vals[0][0] = grid[0][0];
        for (int i = 1; i < rows; ++i) {
     
            vals[i][0] = vals[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < cols; ++j) {
     
            vals[0][j] = vals[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < rows; ++i) {
     
            for (int j = 1; j < cols; ++j) {
     
                vals[i][j] = grid[i][j] + Math.max(vals[i - 1][j], vals[i][j - 1]);
            }
        }
        return vals[rows - 1][cols - 1];
    }
}

JavaScript

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxValue = function (grid) {
     
  let row = grid.length;
  let col = grid[0].length;
  let dp = [...new Array(row + 1)].map(() => Array(col + 1).fill(0));
  for (let i = 1; i <= row; i++) {
     
    for (let j = 1; j <= col; j++) {
     
      dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
    }
  }
  return dp[row][col];
};

…

面试题 48. 最长不含重复字符的子字符串

题目描述

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

示例 1:

输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

提示：

s.length <= 40000

解法

Python3

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        if not s:
            return 0
        cache = {
     }
        cache[s[0]] = 0
        dp = [0 for _ in s]
        dp[0] = res = 1
        for i in range(1, len(s)):
            if s[i] == s[i - 1]:
                dp[i] = 1
            else:
                if cache.get(s[i]) is None:
                    dp[i] = dp[i - 1] + 1
                else:
                    dp[i] = min(dp[i - 1] + 1, i - cache[s[i]])
            cache[s[i]] = i
            res = max(res, dp[i])
        return res

Java

class Solution {
     
    public int lengthOfLongestSubstring(String s) {
     
        if (s == null || "".equals(s)) {
     
            return 0;
        }
        int n = s.length();
        char[] chars = s.toCharArray();
        int[] dp = new int[n];
        int res = 1;
        Map<Character, Integer> map = new HashMap<>();
        dp[0] = 1;
        map.put(chars[0], 0);
        for (int i = 1; i < n; ++i) {
     
            if (chars[i] == chars[i - 1]) {
     
                dp[i] = 1;
            } else {
     
                if (map.get(chars[i]) == null) {
     
                    dp[i] = dp[i - 1] + 1;
                } else {
     
                    dp[i] = Math.min(dp[i - 1] + 1, i - map.get(chars[i]));
                }
            }
            map.put(chars[i], i);
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

JavaScript

/**
 * @param {string} s
 * @return {number}
 */
var lengthOfLongestSubstring = function (s) {
     
  let left = 0;
  let right = 0;
  let res = 0;
  let len = s.length;
  let rec = {
     };
  while (right < len) {
     
    let tmp = "*";
    while (right < len) {
     
      tmp = s[right];
      if (!rec[tmp]) rec[tmp] = 0;
      rec[tmp]++;
      if (rec[tmp] > 1) break;
      right++;
    }
    res = Math.max(res, right - left);
    while (rec[tmp] > 1) rec[s[left++]]--;
    right++;
  }
  return res;
};

C++

class Solution {
     
public:
    int lengthOfLongestSubstring(string s) {
     
        int arr[1024];    // 本题的用例中，有不为小写字母的情况
        for (int i = 0; i < 1024; i++) {
     
            arr[i] = -1;
        }

        int curLen = 0;
        int maxLen = 0;

        int len = s.size();
        for (int i = 0; i < len; i++) {
     
            int prev = arr[int(s[i])];    // 之前位置的index
            if (prev < 0 || i - prev > curLen) {
     
                // 其中，prev>0表示之前没有遇到过该字符
                // i - prev > curLen 表示之前遇到的当前字符，远超当前限定的范围
                // 这两种情况下，都是直接继续加就可以了
                curLen++;
            } else {
     
                if (curLen > maxLen) {
     
                    maxLen = curLen;
                }
                curLen = i - prev;    // curLen重新开始计数
            }

            arr[int(s[i])] = i;
        }

        return maxLen > curLen ? maxLen : curLen;
    }
};

…

面试题 49. 丑数

题目描述

我们把只包含因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

说明:

1 是丑数。
n 不超过 1690。

解法

Python3

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        if n < 7:
            return n
        dp = [1 for _ in range(n)]
        i2 = i3 = i5 = 0
        for i in range(1, n):
            next2, next3, next5 = dp[i2] * 2, dp[i3] * 3, dp[i5] * 5
            dp[i] = min(next2, next3, next5)
            if dp[i] == next2:
                i2 += 1
            if dp[i] == next3:
                i3 += 1
            if dp[i] == next5:
                i5 += 1
        return dp[n - 1]

Java

class Solution {
     
    public int nthUglyNumber(int n) {
     
        if (n < 7) {
     
            return n;
        }
        int[] dp = new int[n];
        dp[0] = 1;
        int i2 = 0, i3 = 0, i5= 0;
        for (int i = 1; i < n; ++i) {
     
            int next2 = dp[i2] * 2, next3 = dp[i3] * 3, next5 = dp[i5] * 5;
            dp[i] = Math.min(Math.min(next2, next3), next5);
            if (dp[i] == next2) {
     
                ++i2;
            }
            if (dp[i] == next3) {
     
                ++i3;
            }
            if (dp[i] == next5) {
     
                ++i5;
            }
        }
        return dp[n - 1];

    }
}

JavaScript

/**
 * @param {number} n
 * @return {number}
 */
var nthUglyNumber = function (n) {
     
  let res = [1];
  //三指针
  let a = 0; //2
  let b = 0; //3
  let c = 0; //5
  let min = 0;
  for (let i = 1; i < n; i++) {
     
    min = Math.min(res[a] * 2, res[b] * 3, res[c] * 5);
    if (min === res[a] * 2) a++;
    if (min === res[b] * 3) b++;
    if (min === res[c] * 5) c++;
    res.push(min);
  }
  return res[n - 1];
};

…

面试题 50. 第一个只出现一次的字符

题目描述

在字符串 s 中找出第一个只出现一次的字符。如果没有，返回一个单空格。

示例:

s = "abaccdeff"
返回 "b"

s = ""
返回 " "
```

**限制：**

- `0 <= s 的长度 <= 50000`

## 解法
有序字典解决。



### **Python3**
```python
import collections

class Solution:
    def firstUniqChar(self, s: str) -> str:
        if s == '':
            return ' '
        cache = collections.OrderedDict()
        for c in s:
            cache[c] = 1 if cache.get(c) is None else cache[c] + 1
        for k, v in cache.items():
            if v == 1:
                return k
        return ' '

Java

class Solution {
     
    public char firstUniqChar(String s) {
     
        if ("".equals(s)) {
     
            return ' ';
        }
        Map<Character, Integer> map = new LinkedHashMap<>();
        char[] chars = s.toCharArray();
        for (char c : chars) {
     
            map.put(c, map.get(c) == null ? 1 : 1 + map.get(c));
        }
        for (Map.Entry<Character, Integer> entry : map.entrySet()) {
     
            if (entry.getValue() == 1) {
     
                return entry.getKey();
            }
        }
        return ' ';
    }
}

JavaScript

/**
 * @param {string} s
 * @return {character}
 */
var firstUniqChar = function (s) {
     
  let t = new Array(26).fill(0);
  let code = "a".charCodeAt();
  for (let i = 0; i < s.length; i++) {
     
    t[s[i].charCodeAt() - code]++;
  }
  for (let i = 0; i < s.length; i++) {
     
    if (t[s[i].charCodeAt() - code] === 1) return s[i];
  }
  return " ";
};

…

面试题 51. 数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

解法

在归并中统计逆序对。

Python3

class Solution:
    def reversePairs(self, nums: List[int]) -> int:
        self.res = 0

        def merge(part1, part2, nums):
            len1, len2 = len(part1) - 1, len(part2) - 1
            t = len(nums) - 1
            while len1 >= 0 and len2 >= 0:
                if part1[len1] > part2[len2]:
                    self.res += (len2 + 1)
                    nums[t] = part1[len1]
                    len1 -= 1
                else:
                    nums[t] = part2[len2]
                    len2 -= 1
                t -= 1
            while len1 >= 0:
                nums[t] = part1[len1]
                t -= 1
                len1 -= 1
            while len2 >= 0:
                nums[t] = part2[len2]
                t -= 1
                len2 -= 1

        def merge_sort(nums):
            if len(nums) < 2:
                return
            mid = len(nums) // 2
            s1, s2 = nums[:mid], nums[mid:]
            merge_sort(s1)
            merge_sort(s2)
            merge(s1, s2, nums)

        merge_sort(nums)
        return self.res

Java

class Solution {
     
    private int res = 0;
    public int reversePairs(int[] nums) {
     
        int n = nums.length;
        if (n < 2) {
     
            return 0;
        }
        mergeSort(nums, 0, n - 1);
        return res;
    }

    private void mergeSort(int[] nums, int s, int e) {
     
        if (s == e) {
     
            return;
        }
        int mid = s + ((e - s) >> 1);
        mergeSort(nums, s, mid);
        mergeSort(nums, mid + 1, e);
        merge(nums, s, mid, e);
    }

    private void merge(int[] nums, int s, int mid, int e) {
     
        int n = e - s + 1;
        int[] help = new int[n];
        int i = s, j = mid + 1, idx = 0;
        while (i <= mid && j <= e) {
     
            if (nums[i] > nums[j]) {
     
                res += (mid - i + 1);
                help[idx++] = nums[j++];
            } else {
     
                help[idx++] = nums[i++];
            }
        }
        while (i <= mid) {
     
            help[idx++] = nums[i++];
        }
        while (j <= e) {
     
            help[idx++] = nums[j++];
        }
        for (int t = 0; t < n; ++t) {
     
            nums[s + t] = help[t];
        }
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @return {number}
 */
var reversePairs = function (nums) {
     
  if (!nums || nums.length < 2) return 0;
  let res = 0;
  function mergeSort(arr) {
     
    if (arr.length === 1) {
     
      return arr;
    }
    let mid = ~~(arr.length / 2);
    return merge(mergeSort(arr.slice(0, mid)), mergeSort(arr.slice(mid)));
  }
  function merge(a, b) {
     
    let r = [];
    let cnt = 0;
    while (a && b && a.length && b.length) {
     
      if (a[0] <= b[0]) {
     
        res += cnt;
        r.push(a.shift());
      } else {
     
        r.push(b.shift());
        cnt++;
      }
    }
    res += a.length * cnt;
    return r.concat(a, b);
  }
  mergeSort(nums);
  return res;
};

…

面试题 52. 两个链表的第一个公共节点

题目描述

输入两个链表，找出它们的第一个公共节点。

如下面的两个链表：

在节点 c1 开始相交。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Reference of the node with value = 2
输入解释：相交节点的值为 2 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
输入解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
解释：这两个链表不相交，因此返回 null。

注意：

如果两个链表没有交点，返回 null。
在返回结果后，两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n) 时间复杂度，且仅用 O(1) 内存。

解法

先求出两个链表的长度差 len1-len2，之后遍历链表，长的链表先走 len1-len2 步。

接着两个链表同时走，当出现相同的节点时，说明两个链表在此节点相交，返回此节点，否则返回 null。

Python3

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        if headA is None or headB is None:
            return None
        len1 = len2 = 0
        p, q = headA, headB
        while p:
            p = p.next
            len1 += 1
        while q:
            q = q.next
            len2 += 1
        p, q = headA, headB
        if len1 > len2:
            p, q = q, p
        for _ in range(abs(len1 - len2)):
            q = q.next
        while p and q:
            if p == q:
                return p
            p = p.next
            q = q.next

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
     
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
     
        if (headA == null || headB == null) {
     
            return null;
        }
        ListNode p = headA, q = headB;
        int len1 = len(p), len2 = len(q);
        if (len1 > len2) {
     
            ListNode t = headA;
            headA = headB;
            headB = t;
        }
        p = headA;
        q = headB;
        for (int i = 0; i < Math.abs(len1 - len2); ++i) {
     
            q = q.next;
        }
        while (p != null && q != null) {
     
            if (p == q) {
     
                return p;
            }
            p = p.next;
            q = q.next;
        }
        return null;
    }

    private int len(ListNode node) {
     
        int len = 0;
        while (node != null) {
     
            node = node.next;
            ++len;
        }
        return len;
    }
}

JavaScript

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} headA
 * @param {ListNode} headB
 * @return {ListNode}
 */
var getIntersectionNode = function (headA, headB) {
     
  let h1 = headA;
  let h2 = headB;
  while (h1 !== h2) {
     
    h1 = h1 === null ? headB : h1.next;
    h2 = h2 === null ? headA : h2.next;
  }
  return h2;
};

C++

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */

class Solution {
     
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
     
        ListNode* a = headA;
        ListNode* b = headB;
        while (a != b) {
     
            /* 这个循环的思路是，a先从listA往后走，如果到最后，就接着从listB走；b正好相反。
               如果有交集的话，a和b会在分别进入listB和listA之后的循环中项目
               如果没有交集的话，则a和b会同时遍历完listA和listB后，值同时为nullptr */
            a = (a == nullptr) ? headB : a->next;
            b = (b == nullptr) ? headA : b->next;
        }

        return a;
    }
};

…

面试题 53 - I. 在排序数组中查找数字 I

题目描述

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

限制：

0 <= 数组长度 <= 50000

解法

Python3

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        if not nums:
            return 0
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + ((r - l) >> 1)
            if nums[m] == target:
                return self._count(nums, l, r, m)
            if nums[m] < target:
                l = m + 1
            else:
                r = m - 1
        return 0

    def _count(self, nums, l, r, m) -> int:
        cnt = 0
        for i in range(m, l - 1, -1):
            if nums[i] == nums[m]:
                cnt += 1
            elif nums[i] < nums[m]:
                break

        for i in range(m + 1, r + 1):
            if nums[i] == nums[m]:
                cnt += 1
            elif nums[i] > nums[m]:
                break
        return cnt

Java

class Solution {
     
    public int search(int[] nums, int target) {
     
        if (nums.length == 0) {
     
            return 0;
        }
        int l = 0, r = nums.length - 1;
        while (l <= r) {
     
            int m = l + ((r - l) >> 1);
            if (nums[m] == target) {
     
                return count(nums, l, r, m);
            }
            if (nums[m] < target) {
     
                l = m + 1;
            } else {
     
                r = m - 1;
            }
        }
        return 0;
    }

    private int count(int[] nums, int l, int r, int m) {
     
        int cnt = 0;
        for (int i = m; i >= l; --i) {
     
            if (nums[i] == nums[m]) {
     
                ++cnt;
            } else if (nums[i] < nums[m]) {
     
                break;
            }
        }
        for (int i = m + 1; i <= r; ++i) {
     
            if (nums[i] == nums[m]) {
     
                ++cnt;
            } else if (nums[i] > nums[m]) {
     
                break;
            }
        }
        return cnt;
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function (nums, target) {
     
  if (!nums || !nums.length) return 0;
  let left = 0;
  let right = nums.length - 1;
  let res = 0;
  while (left < right) {
     
    let mid = left + ~~((right - left) / 2);
    if (nums[mid] < target) {
     
      left = mid + 1;
    } else if (nums[mid] > target) {
     
      right = mid;
    } else {
     
      left = mid;
      right = mid;
      break;
    }
  }
  while (nums[left] === target) {
     
    res++;
    left--;
  }
  while (nums[++right] === target) {
     
    res++;
  }
  return res;
};

…

面试题 53 - II. 0 ～ n-1 中缺失的数字

题目描述

一个长度为 n-1 的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围 0 ～ n-1 之内。在范围 0 ～ n-1 内的 n 个数字中有且只有一个数字不在该数组中，请找出这个数字。

示例 1:

输入: [0,1,3]
输出: 2

示例 2:

输入: [0,1,2,3,4,5,6,7,9]
输出: 8

限制：

1 <= 数组长度 <= 10000

解法

二分法。

Python3

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        if r == 0 or nums[0] == 1:
            return nums[0] ^ 1
        if nums[r] == r:
            return r + 1
        while r - l > 1:
            m = l + ((r - l) >> 1)
            if nums[m] == m:
                l = m
            else:
                r = m
        return nums[r] - 1

Java

class Solution {
     
    public int missingNumber(int[] nums) {
     
        int l = 0, r = nums.length - 1;
        if (r == 0 || nums[0] == 1) {
     
            return nums[0] ^ 1;
        }
        if (nums[r] == r) {
     
            return r + 1;
        }
        while (r - l > 1) {
     
            int m = l + ((r - l) >> 1);
            if (nums[m] == m) {
     
                l = m;
            } else {
     
                r = m;
            }
        }
        return nums[r] - 1;
    }
}

JavaScript

/**
 * @param {number[]} nums
 * @return {number}
 */
var missingNumber = function (nums) {
     
  if (!nums || !nums.length) return 0;
  let left = 0;
  let right = nums.length - 1;
  while (left < right) {
     
    let mid = left + ~~((right - left) / 2);
    if (nums[mid] !== mid) {
     
      right = mid;
    } else {
     
      left = mid + 1;
    }
  }
  return nums[left] === left ? nums.length : left;
};

…

面试题 54. 二叉搜索树的第 k 大节点

题目描述

给定一棵二叉搜索树，请找出其中第 k 大的节点。

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

限制：

1 ≤ k ≤ 二叉搜索树元素个数

解法

先遍历右子树，访问根节点，再遍历左子树。遍历到第 k 个结点时，存储结果。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    t, res = 0, -1
    def kthLargest(self, root: TreeNode, k: int) -> int:
        self.t = k
        self._traverse(root)
        return self.res

    def _traverse(self, node):
        if node:
            self._traverse(node.right)
            self.t -= 1
            if self.t == 0:
                self.res = node.val
                return
            self._traverse(node.left)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    private int t;
    private int res;
    public int kthLargest(TreeNode root, int k) {
     
        t = k;
        traverse(root);
        return res;
    }

    private void traverse(TreeNode node) {
     
        if (node != null) {
     
            traverse(node.right);
            --t;
            if (t == 0) {
     
                res = node.val;
                return;
            }
            traverse(node.left);
        }
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthLargest = function (root, k) {
     
  let res;
  let t = 0;
  function traversal(node) {
     
    if (!node) return;
    traversal(node.right);
    if (++t === k) res = node.val;
    traversal(node.left);
  }
  traversal(root);
  return res;
};

…

面试题 55 - I. 二叉树的深度

题目描述

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

提示：

节点总数 <= 10000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     
    public int maxDepth(TreeNode root) {
     
        if (root == null) {
     
            return 0;
        }
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function (root) {
     
  let res = 0;
  function traversal(node, depth) {
     
    if (!node) {
     
      res = Math.max(res, depth);
      return;
    }
    traversal(node.left, depth + 1);
    traversal(node.right, depth + 1);
  }
  traversal(root, 0);
  return res;
};

C++

class Solution {
     
public:
    int maxDepth(TreeNode* root) {
     
        if (nullptr == root) {
     
            return 0;
        }

        int left = maxDepth(root->left);
        int right = maxDepth(root->right);
        return std::max(left, right) + 1;
    }
};

…

面试题 55 - II. 平衡二叉树

题目描述

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过 1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

返回 true。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false。

限制：

1 <= 树的结点个数 <= 10000

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if root is None: