图像处理作业4——图像金字塔多尺度特征提取（改进版）

实验一 图像多尺度特征提取及特点分析

姓名：Tian YJ

语言：Python 3

IDE：Jupyter Notebook

题目要求：用手机或者相机拍摄图像，利用高斯金字塔和拉普拉斯金字塔提取图像多尺度特征，并总结各自特点。

实现原理：

1. 图像金字塔

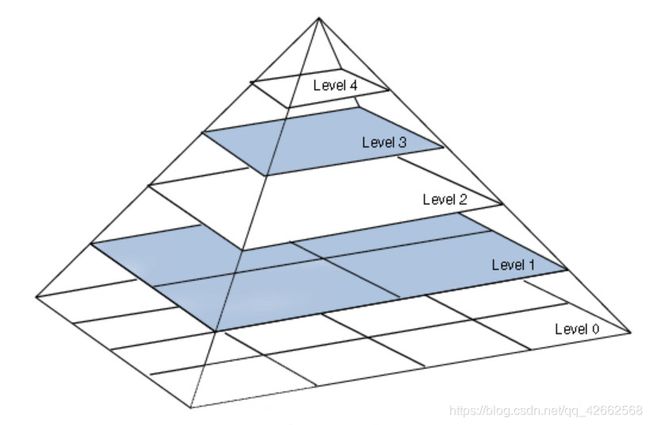
一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似。我们将一层一层的图像比喻成金字塔，层级越高，则图像越小，分辨率越低。就像这样：

2. 如何实现

一般来说，我们可以先讨论两种典型的图像金字塔：高斯金字塔（Gaussian pyramid）和拉普拉斯金字塔（Laplacian pyramid）。

●高斯金字塔(Gaussian pyramid): 高斯金字塔是由底部的最大分辨率图像逐次向下采样得到的一系列图像。最下面的图像分辨率最高，越往上图像分辨率越低。假设$G_0$表示原始图像，$G_i$表示第i次下采样得到的图像，那么高斯金字塔的计算过程可以表示如下：

$$G_i=Down(D_{i-1})$$
其中Down表示下采样函数，下采样可以通过抛去图像中的偶数行和偶数列来实现，这样图像长宽各减少二分之一，面积减少四分之一。

●拉普拉斯金字塔(Laplacian pyramid): 拉普拉斯金字塔可以认为是残差金字塔，用来存储下采样后图片与原始图片的差异。我们知道，如果高斯金字塔中任意一张图$G_i$（比如$G_0$为最初的高分辨率图像）先进行下采样得到图Down($G_i$)，再进行上采样得到图Up(Down($G_i$))，得到的Up(Down($G_i$))与$G_i$是存在差异的，因为下采样过程丢失的信息不能通过上采样来完全恢复，也就是说下采样是不可逆的。下面的公式就是前面的差异记录过程：
$$L_i=G_i-Up(Down(G_i))$$

3. 算法流程

高斯金字塔算法流程：

1. 对图像进行高斯卷积（高斯滤波）
2. 删除偶数行和偶数列（下采样）

拉普拉斯金字塔算法流程：（用于低分辨率恢复高分辨率图像时计算残差）
对于高斯金字塔中的低分辨率图像，

1. 先将图像每个方向放大至原来的两倍（上采样），新增的行和列进行双线性插值代替以0填充
2. 对图像进行高斯卷积（高斯滤波）
3. 用下一层的高分辨率图像减去高斯卷积后的图像

4. 代码实现及结果展示

import numpy as np # 进行数值计算
import matplotlib.pyplot as plt # 绘图
# 我这里用matplotlib画图，就不用先前opencv读取方式
#  (cv2.imread()的通道是按BGR的顺序排列的，plt显示还要交换通道，果断避开)
from skimage.io import imread # 读取图片
# jupyter里加上这一行可以让图像正常显示
%matplotlib inline

# 读取图片
img=imread('Cristiano_Ronaldo.jpg')

K_size = 3 # 滤波器即卷积核的尺寸，这里设置为3*3
pad = K_size // 2 # 需要在图像边缘填充的0行列数，
# 之所以我要这样设置，是为了处理图像边缘时，滤波器中心与边缘对齐

"""
padding 函数
"""

def padding(img):
    # img 为需要处理图像
    # K_size 为滤波器也就是卷积核的尺寸，这里我默认设为3*3，基本上都是奇数

    # 获取图片尺寸
    H, W, C = img.shape
    
    # 先填充行
    rows = np.zeros((pad, W, C), dtype=np.uint8)
    # 再填充列
    cols = np.zeros((H+2*pad, pad, C), dtype=np.uint8)
    # 进行拼接
    img = np.vstack((rows, img, rows)) # 上下拼接
    img = np.hstack((cols, img, cols)) # 左右拼接
    
    # 进行镜像padding，我第一次padding零，出现黑边，边缘失真严重
    # 第一步，上下边框对称取值
    img[0,:,:] = img[2,:,:]
    img[-1,:,:] = img[-3,:,:]
    # 第二步，左右边框对称取值
    img[:,0,:] = img[:,2,:]
    img[:,-1,:] = img[:,-3,:]
    # 第三步，四个顶点对称
    img[0,0,:] = img[0,2,:]
    img[-1,0,:] = img[-1,2,:]
    img[0,-1,:] = img[0,-3]
    img[-1,-1,:] = img[-1,-3,:]
    
    return img

"""
高斯滤波器系数设置
"""
def Kernel(K_sigma=1.3):
    # K_size为滤波器即卷积核尺寸
    # 对滤波器进行初始化0
    K = np.zeros((K_size, K_size), dtype=np.float)

    # 代入公式求高斯滤波器系数，并填入矩阵
    for x in range(-pad, -pad+K_size):
        for y in range(-pad, -pad+K_size):
            K[y + pad, x + pad] = np.exp( -(x ** 2 + y ** 2) / (2 * (K_sigma ** 2)))

    K /= K.sum() # 进行归一化

    return K

"""
高斯滤波函数
"""
def gaussFilter(img):
    # img 为需要处理图像
    # K_size 为滤波器也就是卷积核的尺寸，这里我默认设为3*3，基本上都是奇数

    # 获取图片尺寸
    H, W, C = img.shape

    ## 对图片进行padding
    img = padding(img)

    # 滤波器矩阵
    K =  Kernel()

    ## 进行滤波
    out = img.copy()
    for h in range(H):
        for w in range(W):
            for c in range(C):
                out[pad+h, pad+w, c] = np.sum(K * out[h:h+K_size, w:w+K_size, c])
    # 截取像素合理值
    out = out / out.max() * 255
    out = out[pad: pad + H, pad: pad + W].astype(np.uint8)
    return out

"""
双线性插值函数
"""
def resize(img, ratio=2.):
    # 目标图像尺寸
    new_shape = [
        int(img.shape[0] * ratio),
        int(img.shape[1] * ratio), img.shape[2]
    ]
    result = np.zeros((new_shape))  # 目标图像初始化
    # 遍历新的图像坐标
    for h in range(new_shape[0]):
        for w in range(new_shape[1]):
            # 对应的原图像上的点(向下取整，也就是左上点的位置)
            h0 = int(np.floor(h / ratio))
            w0 = int(np.floor(w / ratio))
            # 新图像的坐标/放缩比例 - 原图像坐标点 = 距离
            dx = h / ratio - h0
            dy = w / ratio - w0
            # 防止溢出
            h1 = h0 + 1 if h0 < img.shape[0] - 1 else h0
            w1 = w0 + 1 if w0 < img.shape[1] - 1 else w0
            # 进行插值计算
            result[h, w] = (1 - dx) * (1 - dy) * img[h0, w0] + dx * (
                1 - dy) * img[h1, w0] + (
                    1 - dx) * dy * img[h0, w1] + dx * dy * img[h1, w1]
    result = result.astype(np.uint8)
    return result

"""
下采样函数
"""
def Down(img):
    # 先进行高斯滤波
    img = gaussFilter(img)
    # 再进行下采样
    H, W, C = img.shape
    H_new = int(np.floor((H+1) / 2))
    W_new = int(np.floor((W+1) / 2 ))
    down = np.zeros((H_new, W_new, C), dtype=np.float)
    for h in range(H_new):
        for w in range(W_new):
            down[h, w, :] = img[2*h, 2*w, :]
    return down

"""
上采样函数
"""

def Up(img):
    # 先进行上采样
    up = resize(img, ratio=2.)
    # 再进行高斯滤波
    up = gaussFilter(up)
    return up

"""
构建高斯金字塔
"""

def gaussian_pyramid(img):
    # img 为原始图像
    pyramids = [img]  # 金字塔数组，用于存放金字塔图片
    new_img = img.copy()

    while True:
        # 原始图像行列数
        cols = new_img.shape[0]
        rows = new_img.shape[1]
        # 目标图像行列数
        new_cols = (cols + 1) // 2
        new_rows = (rows + 1) // 2
        # 尺寸条件判定及结束条件
        if (new_cols * 2 - cols) > 2 or (new_rows * 2 -
                                         rows) > 2 or new_cols < 2 or rows < 2:
            break
        # 高斯滤波
        new_img = gaussFilter(new_img)
        print('======滤波成功======')
        # 进行下采样
        new_img = Down(new_img)
        pyramids.append(new_img)
    return pyramids


# 高斯金字塔显示
pyramid = gaussian_pyramid(img)
print(len(pyramid))
plt.figure(figsize=(30, 5))
plt.suptitle("Guassian Pyramid (8 layers)", fontsize=20)
count = len(pyramid)
for i in range(count):
    ax = plt.subplot(1, count, i + 1)
    ax.set_title(pyramid[i].shape)
    plt.imshow(pyramid[i].astype(np.uint8))
plt.show()

## 我这里想看看如果下采样前不进行高斯滤波是怎么样的效果
"""
下采样函数
"""
def Down(img):
    # 不进行高斯滤波
    # 再进行下采样
    H, W, C = img.shape
    H_new = int(np.floor((H+1) / 2))
    W_new = int(np.floor((W+1) / 2 ))
    down = np.zeros((H_new, W_new, C), dtype=np.float)
    for h in range(H_new):
        for w in range(W_new):
            down[h, w, :] = img[2*h, 2*w, :]
    return down

"""
构建高斯金字塔
"""
def gaussian_pyramid(img):
    # img 为原始图像
    pyramids = [img] # 金字塔数组，用于存放金字塔图片
    new_img = img.copy()

    while True:
        # 原始图像行列数
        cols = new_img.shape[0]
        rows = new_img.shape[1]
        # 目标图像行列数
        new_cols = (cols+1) // 2
        new_rows = (rows+1) // 2
        # 尺寸条件判定及结束条件
        if (new_cols*2-cols)>2 or (new_rows*2-rows)>2 or new_cols<2 or rows<2:
            break
        # 高斯滤波
        new_img = gaussFilter(new_img)
        print('======滤波成功======')
        # 进行下采样
        new_img = Down(new_img)
        pyramids.append(new_img)
    return pyramids

# 高斯金字塔显示
pyramid = gaussian_pyramid(img)
print(len(pyramid))
plt.figure(figsize=(30,5))
plt.suptitle("Guassian Pyramid (8 layers)", fontsize=20)
count=len(pyramid)
for i in range(count):
    ax = plt.subplot(1, count, i+1)
    ax.set_title(pyramid[i].shape)
    plt.imshow(pyramid[i].astype(np.uint8))
plt.show()

从两次结果对比可以看出，如果不进行高斯滤波，图片整体会有些偏暗。

"""
归一化函数
"""

def Normalize(imgIn):
    imgOut = imgIn.copy()
    if imgIn.max() == imgIn.min():
        imgOut = np.zeros(imgIn.shape)
    elif len(imgIn.shape) == 2:
        imgOut = (imgOut - imgOut.min()) / (imgOut.max() - imgOut.min())
    elif len(imgIn.shape) == 3:
        for c in range(3):
            imgOut[:, :, c] = (imgOut[:, :, c] - imgOut[:, :, c].min()) / (
                imgOut[:, :, c].max() - imgOut[:, :, c].min())
    return imgOut

"""
构建拉普拉斯金字塔
"""
def laplacian_pyramid(img):
    ## pyramid为拉普拉斯金字塔每一层图片
    pyramid = [] # 保存拉普拉斯金字塔图片
    newimg = img.astype(np.float)
    
    while True:
        # 原始图像行列数
        imgcols = newimg.shape[0]
        imgrows = newimg.shape[1]
        # 目标图像行列数
        newcols = (imgcols + 1) // 2
        newrows = (imgrows + 1) // 2
        # 尺寸条件判定及结束条件
        if (newcols * 2 - imgcols) > 2 or (
                newrows * 2 - imgrows) > 2 or newcols < 16 or newrows < 16:
            pyramid.append(downSampledImg)
            break
        # 进行下采样
        downSampledImg = Down(newimg)
         # 进行上采样
        upSampledImg = Up(downSampledImg)
        # 计算残差
        resImg = newimg - upSampledImg
        # 循环迭代
        newimg = downSampledImg
        pyramid.append(resImg)
    return pyramid

"""
图像重建
"""
def revertImg(lapPyr):
    # 用于存放重建图像
    revertedImgs = []
    # 图像重建计数
    count = len(lapPyr)
     # 原始图片
    baseImg = lapPyr[-1]
    
    revertedImgs.append(baseImg)
    # 上采样
    baseImg = Up(baseImg)
    
    for i in range(-2, -count, -1):
        # 低一层重建高一层图像+高一层拉普拉斯图像=重建完成图像
        baseImg += lapPyr[i]
        revertedImgs.append(baseImg)
        baseImg = Up(baseImg)
    revertedImgs.append(baseImg)
    return revertedImgs

# 拉普拉斯金字塔及重建图像对比显示
pyramid = laplacian_pyramid(img) # 生成拉普拉斯金字塔
revertedImgs = revertImg(pyramid) # 进行图像重建

plt.figure(figsize=(30, 10))
plt.suptitle("Laplacian Pyramid and Reverted Images", fontsize=30)
count = len(pyramid)

# 绘图显示
for i in range(count):
    # 拉普拉斯金字塔
    ax1 = plt.subplot(2, count, i + 1)
    ax1.set_title(pyramid[i].shape)
    imgToShow = pyramid[i].copy()
    imgToShow = Normalize(imgToShow)
    plt.imshow(imgToShow)

    # 图像重建显示
    ax2 = plt.subplot(2, count, i + 1 + count)
    ax2.set_title(revertedImgs[i].shape)
    imgToShow = revertedImgs[i].copy()
    imgToShow = Normalize(imgToShow)
    plt.imshow(imgToShow)
plt.show()

# 同等比例展示拉普拉斯金字塔
def ShowPyramid(image, maxLevel):
    # 获取图像尺寸
    rows, cols = image.shape[0:2]
    # 构建拉普拉斯金字塔
    imgPyramid = laplacian_pyramid(image)
    # 设置画布大小
    composite_image = np.zeros((rows, cols + cols // 2, 3), dtype=np.double)
    # 进行归一化
    composite_image[:rows, :cols, :] = Normalize(imgPyramid[0])
    # 绘图
    i_row = 0
    for p in imgPyramid[1:]:
        n_rows, n_cols = p.shape[:2]
        composite_image[i_row:i_row + n_rows, cols:cols + n_cols] = Normalize(p)
        i_row += n_rows

    plt.figure(figsize=(15,15))
    plt.title("Laplacian Pyramid")
    plt.imshow(composite_image)
    plt.show()
ShowPyramid(img,6)

5. 结果分析

高斯金字塔中的较高级别（低分辨率）是通过删除较低级别（较高分辨率）图像的行和列形成的。高斯金字塔最底层为图像的原图，通过下采样不断将图像的尺寸缩小为上一个图像的$\frac{1}{4}$，进而在金字塔中包含多个尺度的图像。可以看出，随着下采样的进行，图像的分辨率不断降低，视觉效果也越来越模糊，甚至已经看不出是什么东西了。

拉普拉斯金字塔与高斯金字塔正好相反，高斯金字塔通过底层图像构建上层图像，而拉普拉斯是通过上层小尺寸图像构建下次大尺寸图像。可以看出，原始图片下采样后得到的小尺寸图片虽然保留了视觉效果，但是将该小尺寸图像再次上采样也不能完整的恢复出原始图像。上采样与下采样两者是不可逆的。

为了能够从下采样图像Down($G_i$)中还原原始图像$G_i$，我们需要记录再次上采样得到Up(Down($G_i$))与原始图片$G_i$之间的差异。拉普拉斯金字塔就是记录高斯金字塔每一级下采样后再上采样与下采样前的差异，目的是为了能够完整的恢复出每一层级的下采样前图像。