万向节死锁的理解与CS摄像机减少死锁的简单实现
本文使用glfw库!
一、先摆效果图
二、Unity中的欧拉角
欧拉角有如下两种解释:
1、维基百科上的欧拉角。当认为顺序是YXZ(Yaw->Pitch->Roll)时,是传统的欧拉变换,每次变换都是以物体自己的局部坐标轴进行变换的,可以规避万向节死锁问题。本文后面会给出实现camera的代码。
2、当认为顺序是ZXY(Roll->Pitch->Yaw)的时候,是以惯性坐标系的轴进行变换的。
其中X、Y、Z角分别表示:绕X轴旋转X度,绕Y轴旋转Y度,绕Z轴旋转Z度。
这两种不同的表示,有时候也可以叫做内旋和外旋。
内旋按照旋转后物体的坐标Y轴旋转;
外旋按照世界坐标系中的Y轴旋转。
二、Roll、Pitch、Yaw

沿着机身右方轴(Unity中的+X)进行旋转,称为pitch,中文叫俯仰。
沿着机头上方轴(Unity中的+Y)进行旋转,称为Yaw,中文叫偏航。
沿着机头前方轴(Unity中的+Z)进行旋转,称为Roll,中文叫桶滚。
三、Unity动画演示欧拉角变换和万向锁
(以下出自AndrewFan的文章)
1、欧拉角变换(外旋)
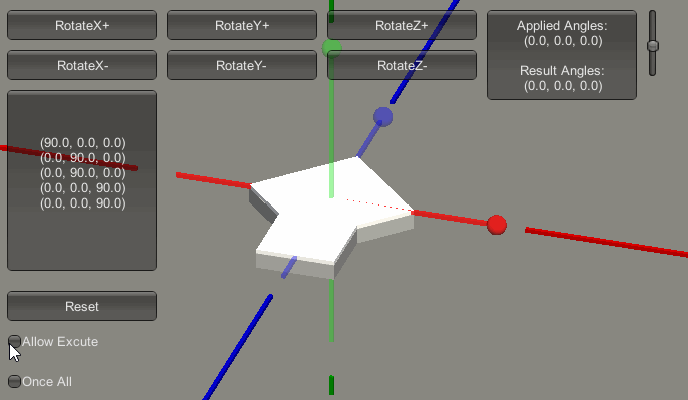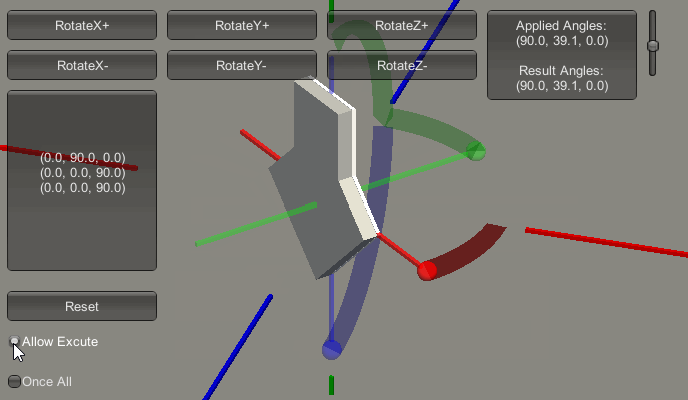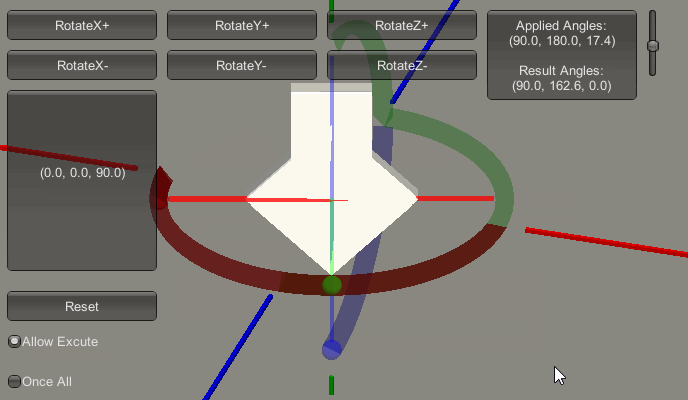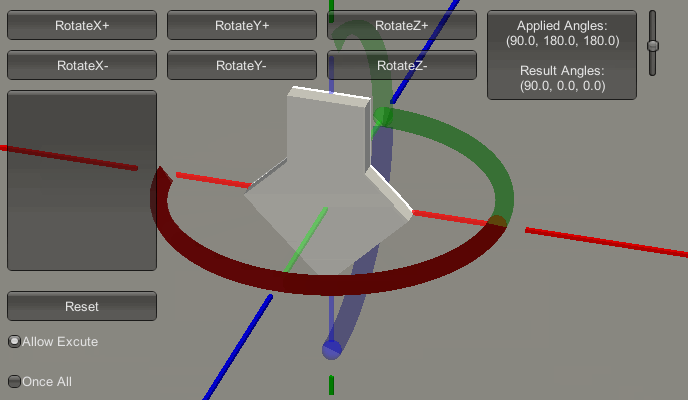
物体的初始状态图(RGB分别对应X轴、Y轴和Z轴):
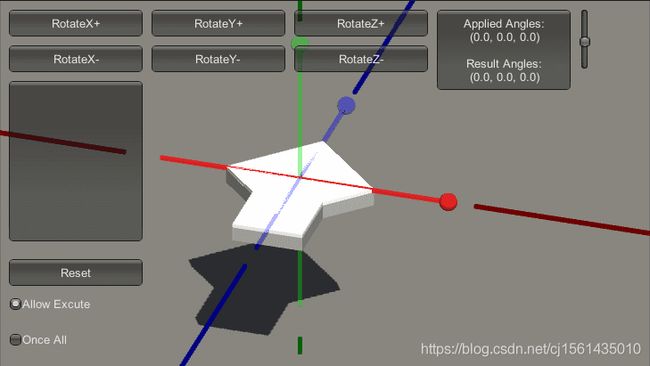
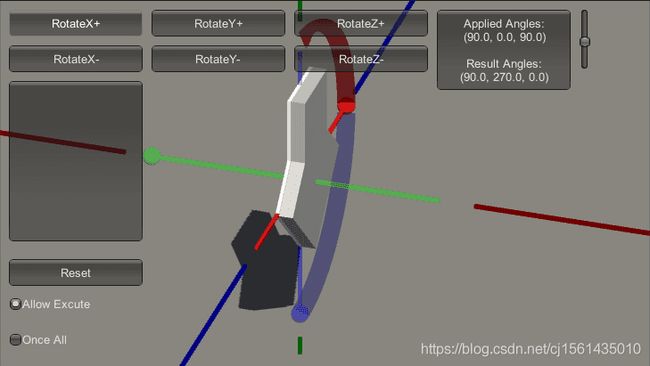
假设我们设定一组欧拉旋转(90,90,90),让unity执行这组欧拉旋转。如下图: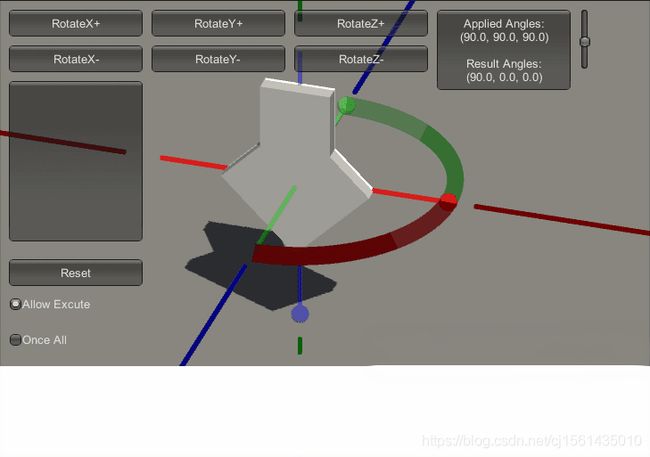
其实Unity引擎是将这一组欧拉变换分成三组去处理的,每次都是相当于从初始状态重新执行累计欧拉角的旋转。
2、验证欧拉角旋转
① 先执行Z轴旋转90度。
四、万向节死锁
本质就是在某一步旋转角度a之后(a%90==0),当前的旋转轴和最开始的世界坐标系恰好重合,但不是完全一模一样。这样会导致本来这样转能做出的旋转方式,现在做出的却是另外一种旋转方式了。
正常情况:
由于Unity中欧拉旋转的顺规的定义,围绕Z轴的进动最先执行,所以就是说,当先沿着Z轴进行进动时,无论此时的XY是什么值,围绕Z轴的旋转方式始终是桶滚。
然而X、Y轴就不同了。先说X轴,如果Z轴也是保持为0,那么围绕X轴进动,最终的影响是预期的俯仰变化。如下图:

异常情况:
然而当Z轴为90度时,围绕X轴的旋转方式变成了偏航。
原因分析:因为Z轴旋转后,物体局部坐标系Y轴的和世界坐标系的X轴重合了,这会导致你怎么转也转不出俯仰这种方式。
结果如下图:

欧拉变换是(90,180,180)时,先绕Z轴旋转180度,再绕X轴旋转90度,最后绕Y轴旋转180度。下图为蜜汁动画,明明是先转Z轴的,不过自己可以拿手机比划一下。
先把手机平放在桌面上,短边平行于你的身子,长边垂直于身子,屏幕朝向天花板。现在将手机绕着短边转90度,现在手机立起来了;紧接着绕长边旋转,你会发现旋转方式只会是滚筒,而本应该是偏航的方式消失了。
原因分析:因为X轴旋转后物体局部坐标系的Z轴和世界坐标系下的Y轴重合了,这会导致你怎么转也转不出偏航这种方式。
四、万向减少节死锁的方法
1、当然是在openGL里面用内旋的方式实现CS的摄像机(就是每次旋转都是相对物体自己的局部坐标系进行旋转变换),但是这涉及到计算视点的算法,该算法就是计算3D中绕任意轴旋转的旋转矩阵。
2、四元数
本来以为万向节死锁可以用内旋的方式解决,听师兄一言才知道是我太天真了。只有用四元数的时候,万向节死锁的情况才会被避免啦!
五、求解旋转矩阵的算法
1总体思路
把v向量沿n向量的方向旋转θ。思路是将v向量分解成垂直于n向量和平行于n向量,对于和n向量平行的向量部分,旋转不起作用。因此将3D旋转的问题简化为2D空间上自行构造出第三个向量,该向量与之前v向量分解出来垂直于n的向量和n都垂直,即这三个向量之间线性无关,将前两者作为基向量,要求的向量可用基向量线性表示。
2、目标
v R ( n , θ ) = v ′ vR(n,\theta )=v^{^{'}} vR(n,θ)=v′,求出旋转矩阵R。
3、符号说明
v v v:初始向量
v ′ v^{'} v′:真正在3D空间中旋转后的向量(要求的目标向量)
v ∣ ∣ v_{||} v∣∣:v向量分解的和n向量平行的向量
n ˉ \bar{n} nˉ:旋转轴(单位向量)
θ \theta θ:旋转角度
v ⊤ v_{\top } v⊤:v向量分解的和n向量垂直的向量
w w w:同时垂直于 v ∣ ∣ v_{||} v∣∣和 v ⊤ v_{\top } v⊤的向量
v ⊤ ′ v_{\top }^{'} v⊤′:将 v ⊤ v_{\top } v⊤在2D空间中旋转 θ \theta θ后的向量
4、 详细推导
v ∣ ∣ = ( v ⋅ n ˉ ) n ˉ v_{||}=(v\cdot \bar{n})\bar{n} v∣∣=(v⋅nˉ)nˉ (ps:点乘的几何意义是投影)
v ∣ ∣ + v ⊤ = v ⇒ v ⊤ = v − ( v ⋅ n ˉ ) n ˉ v_{||}+v_{\top }=v\Rightarrow v_{\top }=v-(v\cdot \bar{n})\bar{n} v∣∣+v⊤=v⇒v⊤=v−(v⋅nˉ)nˉ (ps:可知 v ⊤ v_{\top } v⊤也是单位向量)
v ∣ ∣ + v ⊤ ′ = v ′ v_{||}+v_{\top }^{'}=v^{'} v∣∣+v⊤′=v′
w = n ˉ × v ⊤ = n ˉ × ( v − v ∣ ∣ ) = n ˉ × ( v − ( v ⋅ n ˉ ) n ˉ ) = n ˉ × v w=\bar{n}\times v_{\top }\\=\bar{n}\times (v-v_{||})\\=\bar{n}\times (v-(v\cdot \bar{n})\bar{n})\\=\bar{n}\times v w=nˉ×v⊤=nˉ×(v−v∣∣)=nˉ×(v−(v⋅nˉ)nˉ)=nˉ×v (ps:两个平行向量的叉积是零向量)
假设v向量是单位向量,则有w也是单位向量,因为两个相互垂直的单位向量叉积也是单位向量。
故有: ∥ w ∥ = = ∥ v ⊤ ′ ∥ = = ∥ v ⊤ ∥ \left \| w \right \|==\left \| v_{\top }^{'} \right \|==\left \| v_{\top } \right \| ∥w∥==∥∥∥v⊤′∥∥∥==∥v⊤∥
立即推: v ⊤ ′ = c o s θ ⋅ v ⊤ + s i n θ ⋅ w v_{\top }^{'}=cos\theta \cdot v_{\top }+sin\theta \cdot w v⊤′=cosθ⋅v⊤+sinθ⋅w
⇒ \Rightarrow ⇒ v ′ = v ∣ ∣ + v ⊤ ′ = v ∣ ∣ + c o s θ ⋅ v ⊤ + s i n θ ⋅ w = ( v ⋅ n ˉ ) n ˉ + c o s θ ⋅ ( v − ( v ⋅ n ˉ ) n ˉ ) + s i n θ ⋅ n ˉ × v v^{'}=v_{||}+v_{\top }^{'}\\=v_{||}+cos\theta \cdot v_{\top }+sin\theta \cdot w\\=(v\cdot \bar{n})\bar{n}+cos\theta \cdot (v-(v\cdot \bar{n})\bar{n})+sin\theta \cdot \bar{n}\times v v′=v∣∣+v⊤′=v∣∣+cosθ⋅v⊤+sinθ⋅w=(v⋅nˉ)nˉ+cosθ⋅(v−(v⋅nˉ)nˉ)+sinθ⋅nˉ×v
1、构造基向量一,令 v 1 = [ 1 , 0 , 0 ] T v_{1}=[1,0,0]^{T} v1=[1,0,0]T,
v 1 ′ = ( v ⋅ n ˉ ) n ˉ + c o s θ ⋅ ( v − ( v ⋅ n ˉ ) n ˉ ) + s i n θ ⋅ n ˉ × v = ( [ 1 0 0 ] ⋅ [ n x n y n z ] ) [ n x n y n z ] + c o s θ ⋅ ( [ 1 0 0 ] − ( [ 1 0 0 ] ⋅ [ n x n y n z ] ) [ n x n y n z ] ) + s i n θ ⋅ [ n x n y n z ] × [ 1 0 0 ] = [ n x 2 n x n y n x n z ] + c o s θ ⋅ [ 1 − n x 2 1 − n x n y 1 − n x n z ] + s i n θ ⋅ [ 0 n z − n y ] = [ n x 2 + c o s θ − c o s θ ⋅ n x 2 ) n x n y + c o s θ − c o s θ ⋅ n x n y + s i n θ ⋅ n z n x n z + c o s θ − c o s θ ⋅ n x n z − s i n θ ⋅ n y ] = [ n x 2 ⋅ ( 1 − c o s θ ) + c o s θ n x n y ⋅ ( 1 − c o s θ ) + n z ⋅ s i n θ n x n z ⋅ ( 1 − c o s θ ) − n y ⋅ s i n θ ] v_{1}^{'}=(v\cdot \bar{n})\bar{n}+cos\theta \cdot (v-(v\cdot \bar{n})\bar{n})+sin\theta \cdot \bar{n}\times v\\=(\begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}\cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix} )\begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix}+cos\theta \cdot (\begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}-(\begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}\cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix})\begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix})+sin\theta \cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix}\times \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix}\\=\begin{bmatrix} n_{x}^{2}\\ n_{x}n_{y}\\ n_{x}n_{z} \end{bmatrix}+cos\theta \cdot \begin{bmatrix} 1-n_{x}^{2}\\ 1-n_{x}n_{y}\\ 1-n_{x}n_{z} \end{bmatrix}+sin\theta \cdot \begin{bmatrix} 0\\ n_{z}\\ -n_{y} \end{bmatrix}\\=\begin{bmatrix} n_{x}^{2}+cos\theta -cos\theta \cdot n_{x}^{2})\\ n_{x}n_{y}+cos\theta -cos\theta \cdot n_{x}n_{y}+sin\theta \cdot n_{z}\\ n_{x}n_{z}+cos\theta -cos\theta \cdot n_{x}n_{z}-sin\theta \cdot n_{y} \end{bmatrix}\\=\begin{bmatrix} n_{x}^{2}\cdot (1-cos\theta )+cos\theta \\ n_{x}n_{y}\cdot (1-cos\theta )+n_{z}\cdot sin\theta \\ n_{x}n_{z}\cdot (1-cos\theta )-n_{y}\cdot sin\theta \end{bmatrix} v1′=(v⋅nˉ)nˉ+cosθ⋅(v−(v⋅nˉ)nˉ)+sinθ⋅nˉ×v=(⎣⎡100⎦⎤⋅⎣⎡nxnynz⎦⎤)⎣⎡nxnynz⎦⎤+cosθ⋅(⎣⎡100⎦⎤−(⎣⎡100⎦⎤⋅⎣⎡nxnynz⎦⎤)⎣⎡nxnynz⎦⎤)+sinθ⋅⎣⎡nxnynz⎦⎤×⎣⎡100⎦⎤=⎣⎡nx2nxnynxnz⎦⎤+cosθ⋅⎣⎡1−nx21−nxny1−nxnz⎦⎤+sinθ⋅⎣⎡0nz−ny⎦⎤=⎣⎡nx2+cosθ−cosθ⋅nx2)nxny+cosθ−cosθ⋅nxny+sinθ⋅nznxnz+cosθ−cosθ⋅nxnz−sinθ⋅ny⎦⎤=⎣⎡nx2⋅(1−cosθ)+cosθnxny⋅(1−cosθ)+nz⋅sinθnxnz⋅(1−cosθ)−ny⋅sinθ⎦⎤
2、构造基向量二,令 v 2 = [ 0 , 1 , 0 ] T v_{2}=[0,1,0]^{T} v2=[0,1,0]T,
v 2 ′ = ( v ⋅ n ˉ ) n ˉ + c o s θ ⋅ ( v − ( v ⋅ n ˉ ) n ˉ ) + s i n θ ⋅ n ˉ × v = ( [ 0 1 0 ] ⋅ [ n x n y n z ] ) [ n x n y n z ] + c o s θ ⋅ ( [ 0 1 0 ] − ( [ 0 1 0 ] ⋅ [ n x n y n z ] ) [ n x n y n z ] ) + s i n θ ⋅ [ n x n y n z ] × [ 0 1 0 ] = [ n x n y n y 2 n y n z ] + c o s θ ⋅ [ − n x n y 1 − n y 2 − n y n z ] + s i n θ ⋅ [ − n z 0 n x ] = [ n x n y − c o s θ ⋅ n x n y − s i n θ ⋅ n z n y 2 + c o s θ − c o s θ ⋅ n y 2 n y n z − c o s θ ⋅ n y n z + s i n θ ⋅ n x ] = [ n x n y ⋅ ( 1 − c o s θ ) − n z ⋅ s i n θ n y 2 ⋅ ( 1 − c o s θ ) + c o s θ n y n z ⋅ ( 1 − c o s θ ) + n x ⋅ s i n θ ] v_{2}^{'}=(v\cdot \bar{n})\bar{n}+cos\theta \cdot (v-(v\cdot \bar{n})\bar{n})+sin\theta \cdot \bar{n}\times v\\=(\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}\cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix} )\begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix}+cos\theta \cdot (\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}-(\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}\cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix})\begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix})+sin\theta \cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix}\times \begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}\\=\begin{bmatrix} n_{x}n_{y}\\ n_{y}^{2}\\ n_{y}n_{z} \end{bmatrix}+cos\theta \cdot \begin{bmatrix} -n_{x}n_{y}\\ 1-n_{y}^{2}\\ -n_{y}n_{z} \end{bmatrix}+sin\theta \cdot \begin{bmatrix} -n_{z}\\ 0\\ n_{x} \end{bmatrix}\\=\begin{bmatrix} n_{x}n_{y}-cos\theta \cdot n_{x}n_{y}-sin\theta \cdot n_{z}\\ n_{y}^{2}+cos\theta -cos\theta \cdot n_{y}^{2}\\ n_{y}n_{z}-cos\theta \cdot n_{y}n_{z}+sin\theta \cdot n_{x} \end{bmatrix}\\=\begin{bmatrix} n_{x}n_{y}\cdot (1-cos\theta )-n_{z} \cdot sin\theta\\ n_{y}^{2}\cdot (1-cos\theta )+cos\theta \\ n_{y}n_{z}\cdot (1-cos\theta )+ n_{x} \cdot sin\theta \end{bmatrix} v2′=(v⋅nˉ)nˉ+cosθ⋅(v−(v⋅nˉ)nˉ)+sinθ⋅nˉ×v=(⎣⎡010⎦⎤⋅⎣⎡nxnynz⎦⎤)⎣⎡nxnynz⎦⎤+cosθ⋅(⎣⎡010⎦⎤−(⎣⎡010⎦⎤⋅⎣⎡nxnynz⎦⎤)⎣⎡nxnynz⎦⎤)+sinθ⋅⎣⎡nxnynz⎦⎤×⎣⎡010⎦⎤=⎣⎡nxnyny2nynz⎦⎤+cosθ⋅⎣⎡−nxny1−ny2−nynz⎦⎤+sinθ⋅⎣⎡−nz0nx⎦⎤=⎣⎡nxny−cosθ⋅nxny−sinθ⋅nzny2+cosθ−cosθ⋅ny2nynz−cosθ⋅nynz+sinθ⋅nx⎦⎤=⎣⎡nxny⋅(1−cosθ)−nz⋅sinθny2⋅(1−cosθ)+cosθnynz⋅(1−cosθ)+nx⋅sinθ⎦⎤
3、构造基向量三,令 v 3 = [ 0 , 0 , 1 ] T v_{3}=[0,0,1]^{T} v3=[0,0,1]T,
v 3 ′ = ( v ⋅ n ˉ ) n ˉ + c o s θ ⋅ ( v − ( v ⋅ n ˉ ) n ˉ ) + s i n θ ⋅ n ˉ × v = ( [ 0 0 1 ] ⋅ [ n x n y n z ] ) [ n x n y n z ] + c o s θ ⋅ ( [ 0 0 1 ] − ( [ 0 0 1 ] ⋅ [ n x n y n z ] ) [ n x n y n z ] ) + s i n θ ⋅ [ n x n y n z ] × [ 0 0 1 ] = [ n x n z n y n z n z 2 ] + c o s θ ⋅ [ − n x n z − n y n z 1 − n z 2 ] + s i n θ ⋅ [ n y − n x 0 ] = [ n x n z − c o s θ ⋅ n x n z + s i n θ ⋅ n y n y n z − c o s θ ⋅ n y n z − s i n θ ⋅ n x n z 2 + c o s θ − c o s θ ⋅ n z 2 ] = [ n x n z ⋅ ( 1 − c o s θ ) + n y ⋅ s i n θ n y n z ⋅ ( 1 − c o s θ ) − n x ⋅ s i n θ n z 2 ⋅ ( 1 − c o s θ ) + c o s θ ] v_{3}^{'}=(v\cdot \bar{n})\bar{n}+cos\theta \cdot (v-(v\cdot \bar{n})\bar{n})+sin\theta \cdot \bar{n}\times v\\=(\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}\cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix} )\begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix}+cos\theta \cdot (\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}-(\begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}\cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix})\begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix})+sin\theta \cdot \begin{bmatrix} n_{x}\\ n_{y}\\ n_{z} \end{bmatrix}\times \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}\\=\begin{bmatrix} n_{x}n_{z}\\ n_{y}n_{z}\\ n_{z}^{2} \end{bmatrix}+cos\theta \cdot \begin{bmatrix} -n_{x}n_{z}\\ -n_{y}n_{z}\\ 1-n_{z}^{2} \end{bmatrix}+sin\theta \cdot \begin{bmatrix} n_{y}\\ -n_{x}\\ 0 \end{bmatrix}\\=\begin{bmatrix} n_{x}n_{z}-cos\theta \cdot n_{x}n_{z}+sin\theta \cdot n_{y}\\ n_{y}n_{z}-cos\theta \cdot n_{y}n_{z}-sin\theta \cdot n_{x}\\ n_{z}^{2}+cos\theta -cos\theta \cdot n_{z}^{2} \end{bmatrix}\\=\begin{bmatrix} n_{x}n_{z}\cdot (1-cos\theta )+n_{y} \cdot sin\theta\\ n_{y}n_{z}\cdot (1-cos\theta )-n_{x} \cdot sin\theta\\ n_{z}^{2}\cdot (1-cos\theta )+cos\theta \end{bmatrix} v3′=(v⋅nˉ)nˉ+cosθ⋅(v−(v⋅nˉ)nˉ)+sinθ⋅nˉ×v=(⎣⎡001⎦⎤⋅⎣⎡nxnynz⎦⎤)⎣⎡nxnynz⎦⎤+cosθ⋅(⎣⎡001⎦⎤−(⎣⎡001⎦⎤⋅⎣⎡nxnynz⎦⎤)⎣⎡nxnynz⎦⎤)+sinθ⋅⎣⎡nxnynz⎦⎤×⎣⎡001⎦⎤=⎣⎡nxnznynznz2⎦⎤+cosθ⋅⎣⎡−nxnz−nynz1−nz2⎦⎤+sinθ⋅⎣⎡ny−nx0⎦⎤=⎣⎡nxnz−cosθ⋅nxnz+sinθ⋅nynynz−cosθ⋅nynz−sinθ⋅nxnz2+cosθ−cosθ⋅nz2⎦⎤=⎣⎡nxnz⋅(1−cosθ)+ny⋅sinθnynz⋅(1−cosθ)−nx⋅sinθnz2⋅(1−cosθ)+cosθ⎦⎤
4、用这些基向量构造矩阵, R ( n , θ ) = [ v 1 ′ T v 2 ′ T v 3 ′ T ] = [ n x 2 ⋅ ( 1 − c o s θ ) + c o s θ n x n y ⋅ ( 1 − c o s θ ) + n z ⋅ s i n θ n x n z ⋅ ( 1 − c o s θ ) − n y ⋅ s i n θ n x n y ⋅ ( 1 − c o s θ ) − n z ⋅ s i n θ n y 2 ⋅ ( 1 − c o s θ ) + c o s θ n y n z ⋅ ( 1 − c o s θ ) + n x ⋅ s i n θ n x n z ⋅ ( 1 − c o s θ ) + n y ⋅ s i n θ n y n z ⋅ ( 1 − c o s θ ) − n x ⋅ s i n θ n z 2 ⋅ ( 1 − c o s θ ) + c o s θ ] R(n,\theta )=\begin{bmatrix} v_{1}^{'T}\\ v_{2}^{'T}\\ v_{3}^{'T} \end{bmatrix}=\begin{bmatrix} n_{x}^{2}\cdot (1-cos\theta )+cos\theta & n_{x}n_{y}\cdot (1-cos\theta )+n_{z} \cdot sin\theta &n_{x}n_{z}\cdot (1-cos\theta )-n_{y} \cdot sin\theta \\ n_{x}n_{y}\cdot (1-cos\theta )-n_{z}\cdot sin\theta & n_{y}^{2}\cdot (1-cos\theta )+cos\theta & n_{y}n_{z}\cdot (1-cos\theta )+n_{x} \cdot sin\theta\\ n_{x}n_{z}\cdot (1-cos\theta )+n_{y}\cdot sin\theta & n_{y}n_{z}\cdot (1-cos\theta )- n_{x} \cdot sin\theta & n_{z}^{2}\cdot (1-cos\theta )+cos\theta \end{bmatrix} R(n,θ)=⎣⎡v1′Tv2′Tv3′T⎦⎤=⎣⎡nx2⋅(1−cosθ)+cosθnxny⋅(1−cosθ)−nz⋅sinθnxnz⋅(1−cosθ)+ny⋅sinθnxny⋅(1−cosθ)+nz⋅sinθny2⋅(1−cosθ)+cosθnynz⋅(1−cosθ)−nx⋅sinθnxnz⋅(1−cosθ)−ny⋅sinθnynz⋅(1−cosθ)+nx⋅sinθnz2⋅(1−cosθ)+cosθ⎦⎤
六、代码实现CS摄像机
摄像机代码块:
#include #include "ncamera.h"
nCamera::nCamera() :mPos(-4.0f, 2.0f, -1.0f),mViewCenter(0.0f, 0.0f, -1.0f),mUp(0.0f, 1.0f, 0.0f)
{
mbMoveLeft=false;
mbMoveRight=false;
mbMoveForward=false;
mbMoveBackward=false;
}
void nCamera::RotateView(float angle, float x, float y, float z)
{
//算法实现
glm::vec3 viewDirection=mViewCenter-mPos;
glm::vec3 newDirection;
float C=cosf(angle);
float S=sinf(angle);
glm::vec3 tempX(C+x*x*(1-C),x*y*(1-C)+z*S,x*z*(1-C)-y*S);
newDirection.x = glm::dot(tempX,viewDirection);
glm::vec3 tempY(x*y*(1-C)-z*S, C+y*y*(1-C), y*z*(1-C)+x*S);
newDirection.y = glm::dot(tempY,viewDirection);
glm::vec3 tempZ(x*z*(1 - C) +y*S,y*z*(1 - C)-x*S, C + z*z*(1-C));
newDirection.z = glm::dot(tempZ,viewDirection);
mViewCenter=newDirection+mPos;
}
void nCamera::Yaw(float angle)
{
RotateView(angle,mUp.x,mUp.y,mUp.z);
}
void nCamera::Pitch(float angle)
{
glm::vec3 viewDirection=mViewCenter-mPos;
glm::normalize(viewDirection);
glm::vec3 rightDirection=glm::cross(viewDirection,mUp);
glm::normalize(rightDirection);
RotateView(angle,rightDirection.x,rightDirection.y,rightDirection.z);
}
void nCamera::Update(float deltaTime)
{
float moveSpeed = 10.0f;
float rotateSpeed = 1.0f;
if (mbMoveLeft)
{
glm::vec3 viewDirection = mViewCenter - mPos;
glm::normalize(viewDirection);
glm::vec3 rightDirection = glm::cross(viewDirection,mUp);
glm::normalize(rightDirection);
mPos = mPos + rightDirection*moveSpeed*deltaTime*-1.0f;
mViewCenter = mViewCenter + rightDirection*moveSpeed*deltaTime*-1.0f;
}
if (mbMoveRight)
{
glm::vec3 viewDirection = mViewCenter - mPos;
glm::normalize(viewDirection);
glm::vec3 rightDirection = glm::cross(viewDirection,mUp);
glm::normalize(rightDirection);
mPos = mPos + rightDirection*moveSpeed*deltaTime;
mViewCenter = mViewCenter + rightDirection*moveSpeed*deltaTime;
}
if (mbMoveForward)
{
glm::vec3 forwardDirection=mViewCenter-mPos;
glm::normalize(forwardDirection);
mPos = mPos + forwardDirection*moveSpeed*deltaTime;
mViewCenter = mViewCenter + forwardDirection*moveSpeed*deltaTime;
}
if (mbMoveBackward)
{
glm::vec3 backwardDirection= mPos - mViewCenter;
glm::normalize(backwardDirection);
mPos = mPos + backwardDirection*moveSpeed*deltaTime;
mViewCenter = mViewCenter + backwardDirection*moveSpeed*deltaTime;
}
ViewMatrix=glm::lookAt(mPos,mViewCenter,mUp);
}
windows窗体交互代码:
#include shader生成跳棋棋盘(mesh+简单的异或算法):
顶点着色器:
#version 330 core
layout (location = 0) in vec3 position;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
out vec2 coord;
out vec3 n_p;
void main()
{
vec3 new_pos=position;
gl_Position = projection*view*model*vec4(new_pos, 1.0f);
n_p=new_pos;
}
片段着色器:
GLSL里面不存在隐式转换,需要将int强转成bool。算法思路就是X和Z坐标里面只有一个是偶数的时候,将这个格子渲染成黑色;同奇同偶的时候,将这个格子渲染成白色。
#version 330 core
out vec4 FragColor;
in vec3 n_p;
void main()
{
int x=int(n_p.x),z=int(n_p.z);
if(bool((x%2)^(z%2)))
//if(x%2==1&&z%2==0)
FragColor=vec4(0.0f,0.0f,0.0f,1.0f);
else
FragColor=vec4(1.0f,1.0f,1.0f,1.0f);
}
参考文章: https://blog.csdn.net/AndrewFan/article/details/60981437
参考书籍: 3DMathPrimerForGraphicsAndGameDevelopment
CG的下一篇打算写粒子系统,至于四元数有空再学习,学明白了就会写博客。希望大家支持!