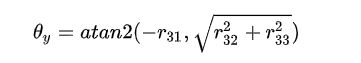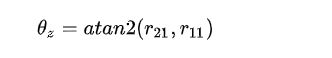3D数学基础——矩阵、欧拉角和四元数的相互转换与比较
矩阵、欧拉角和四元数的相互转换与比较
相互转换
这里只展示最终的转换结果,推导过程请参考《3D数学基础:图形与游戏开发》
欧拉角转换到矩阵
欧拉角描述了一个旋转序列,分别计算出给每个旋转的矩阵再将他们按照一定的顺序连接成一个矩阵,这个矩阵就代表了整个角位移:
矩阵转换到欧拉角
将矩阵表示的角位移转化为欧拉角的表示:
四元数转换到矩阵
四元数q(w,x,y,z)对应的旋转矩阵可以表示为如下形式:![]()
矩阵转换到四元数
利用四元数转换的成的矩阵(上述的矩阵)计算对角线元素之和即可求的 w 值:![]()
利用类似的方法可以计算 x,y,z 的值:![]()
![]()
![]()
以上方式并不总是正常工作,因为平方根的结果的结果总是正值,同时利用一下技巧是检查相对于对角线的对称位置上元素的和与差:
![]()
因此,一旦用对角线元素和/差的平方根解的4个值中的一个,就能利用如下方式计算其他三个:
似乎最简单的策略就是总是先计算同一个分量,如 w,然后再计算 x,y,z 。这样的方式可能存在如下错误:如果 w=0,除法就没有意义(分母不能为0);如有w非常小,将会出现数值不稳定。有学者建议首先判断 w,x,y,z 中哪一个最大,就用对角线元素计算该元素,然后再通过它计算其他三个分量。
//输入矩阵
float m11,m12,m13;
float m21,m22,m23;
float m31,m32,m33;
//输出的四元数
float w,x,y,z;
//探测w,x,y,z 中的最大值
float fourWSquaredMinusl = m11+m22+m33;
float fourXSquaredMinusl = m11-m22-m33;
float fourYSquaredMinusl = m22-m11-m33;
float fourZSquaredMinusl = m33-m11-m22;
int biggestIndex = 0;
float fourBiggestSqureMinus1 = fourWSquaredMinusl;
if(fourXSquaredMinusl>fourBiggestSqureMinus1){
fourBiggestSqureMinus1 = fourXSquaredMinusl;
biggestIndex =1;
}
if(fourYSquaredMinusl>fourBiggestSqureMinus1){
fourBiggestSqureMinus1 = fourYSquaredMinusl;
biggestIndex =2;
}
if(fourZSquaredMinusl>fourBiggestSqureMinus1){
fourBiggestSqureMinus1 = fourZSquaredMinusl;
biggestIndex =3;
}
//计算平方根和除法
float biggestVal = sqrt(fourBiggestSqureMinus1+1.0f)*0.5f;
float mult = 0.25f/biggestVal;
//计算四元数的值
switch(biggestIndex){
case 0:
w=biggestVal;
x=(m23-m32)*mult;
y=(m31-m13)*mult;
z=(m12-m21)*mult;
break;
case 1:
x = biggestVal;
w =(m23-m32)*mult;
y =(m12+m21)*mult;
z =(m31+m13)*mult;
break;
case 2:
y =biggestVal;
w =(m31-m13)*mult;
x =(m12+m21)*mult;
z =(m23+m32)*mult;
break;
case 3:
z =biggestVal;
w =(m12-m21)*mult;
x =(m31+m13)*mult;
y =(m23+m32)*mult;
break;
}
欧拉角转换到四元数
给定一个欧拉旋转(Z-Y-X顺序),则对应的四元数为:q = (w , x, y, z )其中:
四元数转换到欧拉角
根据上面的公式可以求出逆解,即由四元数q=(q0,q1,q2,q3)或q=(w,x,y,z)到欧拉角的转换为:
由于arctan和arcsin的取值范围在−π2−π2和π2π2之间,只有180°,而绕某个轴旋转时范围是360°,因此要使用atan2函数代替arctan函数:
将四元数转为欧拉角可以参考下面的代码。需要注意欧拉角有12种旋转次序,而上面推导的公式是按照Z-Y-X顺序进行的,所以有时会在网上看到不同的转换公式(因为对应着不同的旋转次序),在使用时一定要注意旋转次序:
///
// Quaternion to Euler
///
enum RotSeq{zyx, zyz, zxy, zxz, yxz, yxy, yzx, yzy, xyz, xyx, xzy,xzx};
void twoaxisrot(double r11, double r12, double r21, double r31, double r32, double res[]){
res[0] = atan2( r11, r12 );
res[1] = acos ( r21 );
res[2] = atan2( r31, r32 );
}
void threeaxisrot(double r11, double r12, double r21, double r31, double r32, double res[]){
res[0] = atan2( r31, r32 );
res[1] = asin ( r21 );
res[2] = atan2( r11, r12 );
}
void quaternion2Euler(const Quaternion& q, double res[], RotSeq rotSeq)
{
switch(rotSeq){
case zyx:
threeaxisrot( 2*(q.x*q.y + q.w*q.z),
q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
-2*(q.x*q.z - q.w*q.y),
2*(q.y*q.z + q.w*q.x),
q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
res);
break;
case zyz:
twoaxisrot( 2*(q.y*q.z - q.w*q.x),
2*(q.x*q.z + q.w*q.y),
q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
2*(q.y*q.z + q.w*q.x),
-2*(q.x*q.z - q.w*q.y),
res);
break;
case zxy:
threeaxisrot( -2*(q.x*q.y - q.w*q.z),
q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
2*(q.y*q.z + q.w*q.x),
-2*(q.x*q.z - q.w*q.y),
q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
res);
break;
case zxz:
twoaxisrot( 2*(q.x*q.z + q.w*q.y),
-2*(q.y*q.z - q.w*q.x),
q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
2*(q.x*q.z - q.w*q.y),
2*(q.y*q.z + q.w*q.x),
res);
break;
case yxz:
threeaxisrot( 2*(q.x*q.z + q.w*q.y),
q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
-2*(q.y*q.z - q.w*q.x),
2*(q.x*q.y + q.w*q.z),
q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
res);
break;
case yxy:
twoaxisrot( 2*(q.x*q.y - q.w*q.z),
2*(q.y*q.z + q.w*q.x),
q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
2*(q.x*q.y + q.w*q.z),
-2*(q.y*q.z - q.w*q.x),
res);
break;
case yzx:
threeaxisrot( -2*(q.x*q.z - q.w*q.y),
q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
2*(q.x*q.y + q.w*q.z),
-2*(q.y*q.z - q.w*q.x),
q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
res);
break;
case yzy:
twoaxisrot( 2*(q.y*q.z + q.w*q.x),
-2*(q.x*q.y - q.w*q.z),
q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
2*(q.y*q.z - q.w*q.x),
2*(q.x*q.y + q.w*q.z),
res);
break;
case xyz:
threeaxisrot( -2*(q.y*q.z - q.w*q.x),
q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
2*(q.x*q.z + q.w*q.y),
-2*(q.x*q.y - q.w*q.z),
q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
res);
break;
case xyx:
twoaxisrot( 2*(q.x*q.y + q.w*q.z),
-2*(q.x*q.z - q.w*q.y),
q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
2*(q.x*q.y - q.w*q.z),
2*(q.x*q.z + q.w*q.y),
res);
break;
case xzy:
threeaxisrot( 2*(q.y*q.z + q.w*q.x),
q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
-2*(q.x*q.y - q.w*q.z),
2*(q.x*q.z + q.w*q.y),
q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
res);
break;
case xzx:
twoaxisrot( 2*(q.x*q.z - q.w*q.y),
2*(q.x*q.y + q.w*q.z),
q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
2*(q.x*q.z + q.w*q.y),
-2*(q.x*q.y - q.w*q.z),
res);
break;
default:
std::cout << "Unknown rotation sequence" << std::endl;
break;
}
}
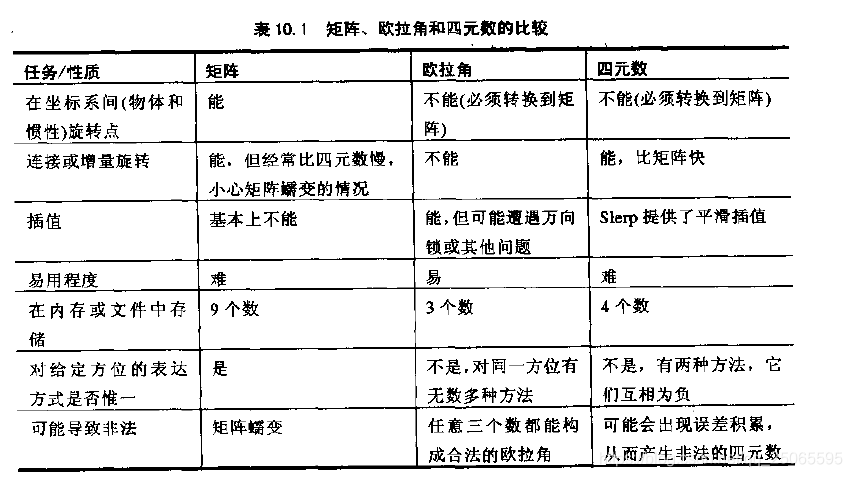
方位表示比较
矩阵
优点
- 可以立即进行向量的旋转;
- 矩阵的形式被图形API所使用;当和图形API交流时,最终必须用矩阵来描述所需的转换;
- 矩阵的组合实现多个角位移的连接;
- 逆矩阵就是“相反"的角位移,因为旋转矩阵是正交的,而正交矩阵的逆矩阵等于 转置矩阵。
缺点
- 矩阵占用更多的空间,欧拉角只需要三个数字来表达方位,而矩阵需要9个;
- 难于使用,由于矩阵很不直观;
- 描述方位的矩阵必须满足限制条件:行必须是单位向量,并且各行相互垂直,但是矩阵可能是病态的(比如精度的缺失,导致不满足上述条件)。
欧拉角
优点:
- 欧拉角中的数都是角度,很直观,所以欧拉角很容易使用;
- 最简洁的表示方式,仅使用三个数来表达方位
- 任意三个数都是合法的
缺点:
- 给定方位的表达方式不唯一
- 二个角度间的插值非常困难
- 万向节死锁问题
四元数
优点
- 四元数可以平滑插值(球面线性插值)
- 四元数的叉乘能将角位移序列快速转换为单个角位移,并很容易实现角位移的求逆
- 能和矩阵形式快速转换
缺点
- 相比欧拉角数据量要大一些
- 四元数可能出现不合法
- 四元数是最难于使用的
总结
- 欧拉角最容易使用:大大简化人机交互(包括直接的键盘输入方位、渲染中指定的摄像机、调试测试等);
- 如果需要在坐标系之间转换向量,那么选择矩阵形式;
- 当需要保存大量的方位数据时,使用欧拉角或者四元数;
- 平滑的插值只能通过四元数来实现
以上参考:
- 3D数学基础:图形于游戏开发
- 游戏引擎架构
- https://blog.csdn.net/loongkingwhat/article/details/88428310
- https://www.cnblogs.com/21207-iHome/p/6894128.html