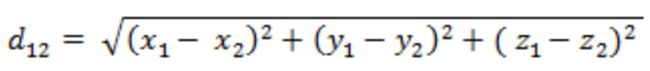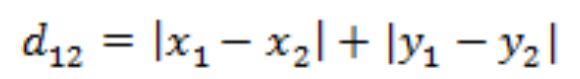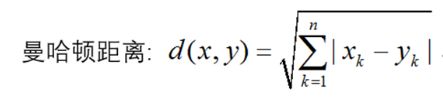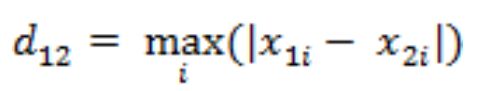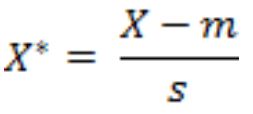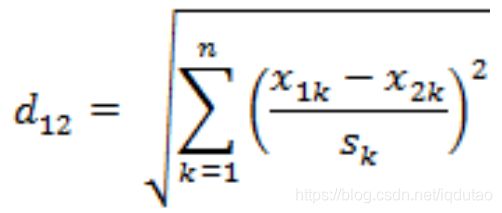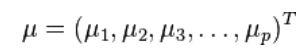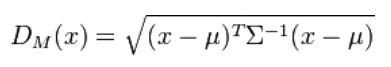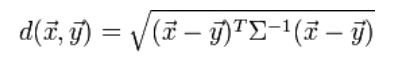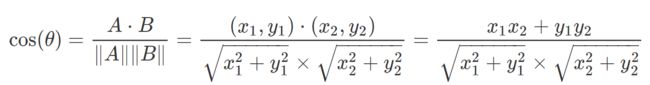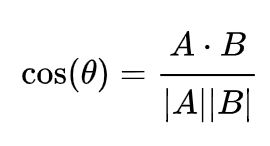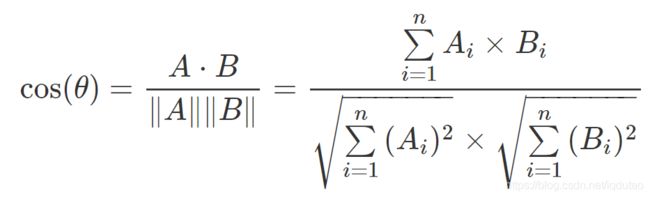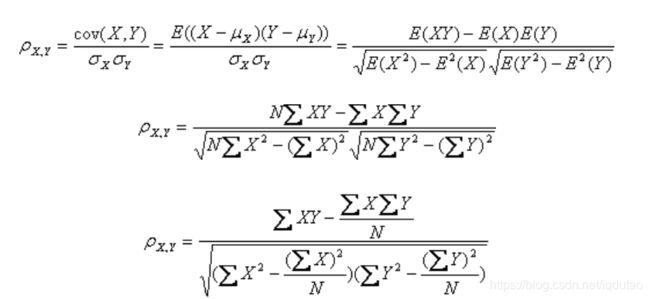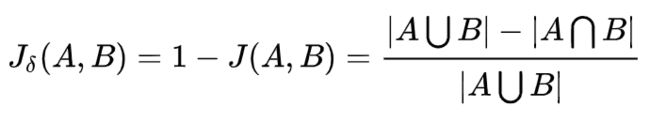机器学习-距离度量和相似度计算

 

       在机器学习和数据挖掘中，我们经常需要知道个体间差异的大小，进而评价个体的相似性和类别。最常见的是数据分析中的相关分析，数据挖掘中的分类和聚类算法，在机器学习中聚类算法，如最近邻（KNN）和 K 均值（K-Means）或者分类任务中，需要度量样本间的距离或者相似度；在推荐系统中，基于内容的过滤算法和协同过滤算法都使用了某种特定的相似度度量来确定两个用户或商品的向量之间的相等程度，都需要进行相关的度量方式。

目录

1. 欧氏距离(Euclidean  Distance)

2. 曼哈顿距离(Manhattan Distance) 

3. 切比雪夫距离 (Chebyshev Distance)

4. 闵可夫斯基距离(Minkowski Distance）

5. 标准化欧氏距离 (Standardized Euclidean Distance)

6. 马氏距离(Mahalanobis Distance)

7. 余弦距离(Cosine Distance)

8. 汉明距离(Hamming Distance)

9. 皮尔森相关系数（Pearson Correlation）

        10. 杰卡德距离(Jaccard Distance)

---

1. 欧氏距离(Euclidean  Distance)

定义：欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”（即直线）距离。

欧式距离是最容易直观理解的距离度量方法，欧式距离是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。

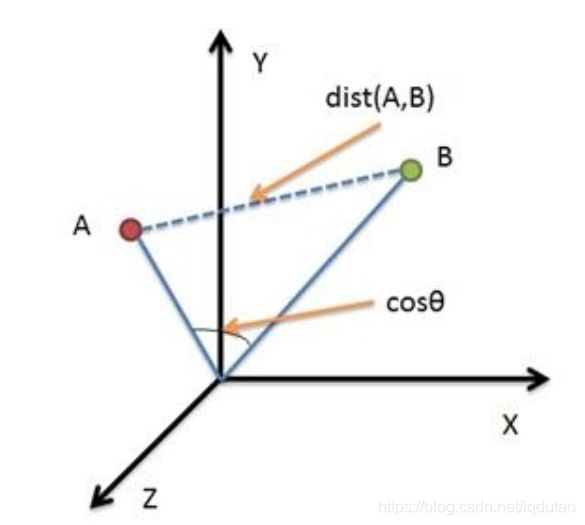
例1  二维平面上点a(x1,y1)与b(x2,y2)间的欧氏距离:

                          

  A和B之间的距离表示为： 

                           

 欧式距离示例计算过程为：

                     

例2  三维空间点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:

                           

                          

例3  n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离（两个n维向量）：

                               

欧式距离的Python实现

import numpy as np


vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])

#在数据完整(无维度数据缺失)的情况下, 维度间的衡量单位是一致的, 否则需要标准化处理

d = np.linalg.norm(vec1-vec2, ord=2)
# 或者
d = np.sqrt(np.sum(np.square(vec1-vec2)))

 

2. 曼哈顿距离(Manhattan Distance) 

定义：在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和，即两个点在标准坐标系上的绝对轴距总和。

想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾 驶距离就是这个“曼哈顿距离”,也称为城市街区距离(City Block distance)。

            

例1  二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离：

                                     

曼哈顿距离示例计算过程为：

                                

例2  n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离：

                  

曼哈顿距离Python实现

import numpy as np

vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])
 
d = np.linalg.norm(vec1-vec2, ord=1)
# 或者
d = np.sum(np.abs(vec1-vec2))

 

3. 切比雪夫距离 (Chebyshev Distance)

定义：切比雪夫距离是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。

切比雪夫距离也叫棋盘距离（ChessboardDistance）或L-Infinity距离。国际象棋中，对该距离最简单的解释就是“王”在棋盘上移动的距离：可以朝任意方向走（上、下、左、右），国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。切比雪夫距离中，走斜线跟走直角是一样的，所以各坐标数值差的最大值。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？

                      

例1  二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离：

                             

 切比雪夫距离示例计算过程为：

                      

例2  n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离

                               

切比雪夫距离Python代码实现

import numpy as np

vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])

d = np.linalg.norm(vec1-vec2, ord=np.inf)
# 或者
d = np.abs(vec1-vec2).max()

 

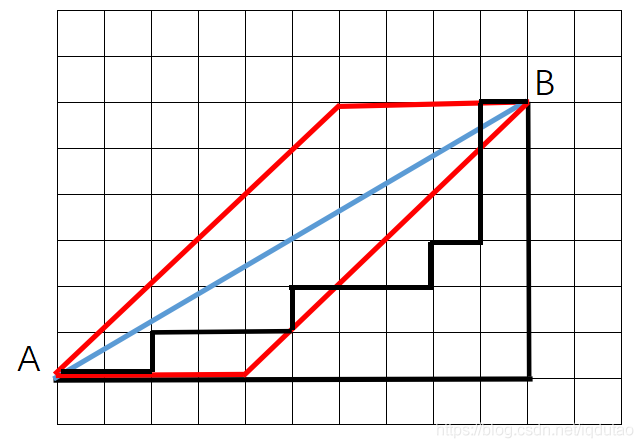
欧氏距离、曼哈顿距离和切比雪夫距离的对比

蓝色的斜线表示欧几里得距离，表示两点之间的直线距离；

黑色的折线表示曼哈顿距离，只能走直线，并且这三条折线的长度是相等的；

红色的路径表示切比雪夫距离，可以走直线，可以走斜线，但是只能沿着方格的顶点走；

                

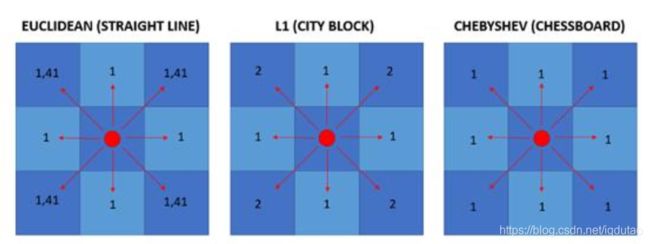
每步长度对比如下图所示，分别对应欧氏距离、曼哈顿距离和切比雪夫距离的每步长度

         

 

4. 闵可夫斯基距离(Minkowski Distance）

闵氏距离定义：闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

                                     

其中p是一个变参数：

当p=1时，就是曼哈顿距离；

当p=2时，就是欧氏距离；

当p→∞时，就是切比雪夫距离。

因此，根据变参数的不同，闵氏距离可以表示某一类/种的距离。

闵可夫斯基距离Python代码实现

import numpy as np

vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])

"""
ord=1: 一范数
ord=2: 二范数
ord=np.inf: 无穷范数
"""
d = np.linalg.norm(vec1-vec2, ord=arg)

 

5. 标准化欧氏距离 (Standardized Euclidean Distance)

定义： 标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。标准欧氏距离的思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。

假设样本集X的均值(mean)为m，标准差(standard deviation)为s，X的“标准化变量”表示为：

                                             

标准化欧氏距离公式：

                                    

如果将方差的倒数看成一个权重，也可称之为加权欧氏距离(Weighted Euclidean distance)。

 

6. 马氏距离(Mahalanobis Distance)

概念：马氏距离(Mahalanobis Distance)是度量学习中一种常用的距离指标，同欧氏距离、曼哈顿距离、汉明距离等一样被用作评定数据之间的相似度指标，但却可以应对高维线性分布的数据中各维度间非独立同分布的问题。所以马氏距离是基于样本分布的一种距离。物理意义就是在规范化的主成分空间中（对原始数据修正后）的欧氏距离，所谓规范化的主成分空间就是利用主成分分析对一些数据进行主成分分解，再对所有主成分分解轴做归一化，形成新的坐标轴，由这些坐标轴张成的空间就是规范化的主成分空间。   

例1  在概率论中，两个随机变量 X 与 Y 之间相互关系，大致有下列3种情况：       

当 X, Y 的联合分布像左图那样时，大致上有： X 越大 Y 也越大， X 越小 Y 也越小，这种情况，我们称为“正相关”。

当X, Y 的联合分布像中间图那样时，大致上有：X 越大Y 反而越小，X 越小 Y 反而越大，这种情况，我们称为“负相关”。

当X, Y 的联合分布像右图那样时，既不是X 越大Y 也越大，也不是 X 越大 Y 反而越小，这种情况我们称为“不相关”。

同样将这3种相关情况，用一个简单的数字表达出来呢？

在图中的区域（1）中，有 X>EX ，Y-EY>0 ，所以(X-EX)(Y-EY)>0；

在图中的区域（2）中，有 X0 ，所以(X-EX)(Y-EY)<0；

在图中的区域（3）中，有 X0；

在图中的区域（4）中，有 X>EX ，Y-EY<0 ，所以(X-EX)(Y-EY)<0。

当X 与Y 正相关时，分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有E(X-EX)(Y-EY)>0 。

当 X与 Y负相关时，分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有(X-EX)(Y-EY)<0。

当 X与 Y不相关时，在区域（1）和（3）中的分布，与在区域（2）和（4）中的分布一样多，平均来说，有(X-EX)(Y-EY)=0。

所以，我们可以定义一个表示X, Y 相互关系的数字特征，也就是协方差，即cov(X, Y) = E(X-EX)(Y-EY)。

当 cov(X, Y)>0时，表明X与Y 正相关；

当 cov(X, Y)<0时，表明X与Y负相关；

当 cov(X, Y)=0时，表明X与Y不相关。

这就是协方差的意义。

 

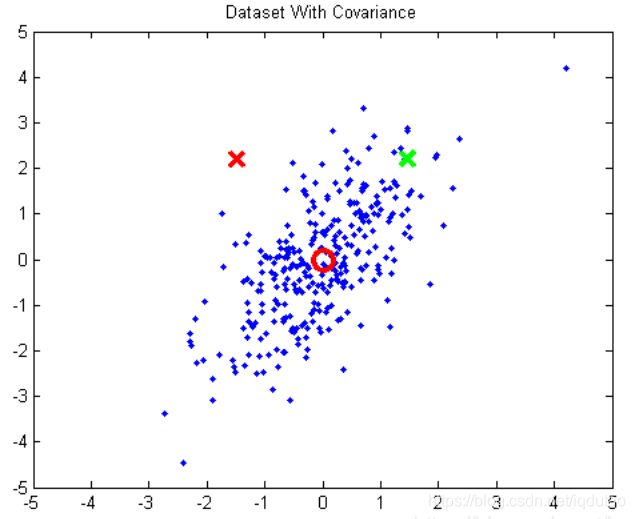
例2  下面是一个二维空间中距离度量的例子

                            

图中，圆圈表示样本分布的中心点c，两个叉分别表示两个样本点x,y，可以看出，在二维空间中两个叉到样本分布的中心点间的欧氏距离相等。但是很明显，绿叉应该是分布内的点，红叉是分布外的点，所以绿叉距离分布中心点的距离应该更近才合理。

使用马氏距离，就等同于通过数据转换的方法，消除样本中不同特征维度间的相关性和量纲差异，使的欧式距离在新的分布上能有效度量样本到分布间的距离。

第一步，端详一下原始数据分布的特点。
这些样本的特征维度即为横坐标轴和纵坐标轴，且两个特征维度呈现明显的正相关性。

第二步，消除不同维度之间的相关性。
消除特征维度间的相关性后，样本分布图如下所示，还存在的一个问题是两个特征维度间的量纲不一致。

                             

第三步，消除不同维度之间的量纲差异。

                                

经过以上三步，现在的样本分布下，样本间的距离可以用欧氏距离来衡量。

 

例3  如上图，看左下方的图，比较中间那个绿色的和另外一个绿色的距离，以及中间绿色到蓝色的距离：

                      

 

如果不考虑数据的分布，就是直接计算欧式距离，那就是蓝色距离更近

但实际上需要考虑各分量的分布的，呈椭圆形分布

蓝色的在椭圆外，绿色的在椭圆内，因此绿色的实际上更近

马氏距离除以了协方差矩阵，实际上就是把右上角的图变成了右下角

  

        马氏距离表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。 对于一个均值为

                                

协方差矩阵为Σ的多变量矢量

                                  

其马氏距离为

                             

马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量X与Y的差异程度：

                           

如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离；如果协方差矩阵为对角阵，其也可称为正规化的马氏距离，其中σi是xi的标准差。

                              

       马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同。在计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧氏距离计算即可。满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，如三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧氏距离计算。

 

7. 余弦距离(Cosine Distance)

       余弦相似度，又称为余弦相似性，是通过计算两个向量的夹角余弦值来评估他们的相似度，相似度度量的值越小，说明个体间相似度越小，相似度的值越大说明个体差异越大。在几何中，夹角余弦可用来衡量两个向量方向的差异；在机器学习中，借用这一概念来衡量样本向量之间的差异。

       对于多个不同的文本或者短文本对话消息要来计算他们之间的相似度如何，一个好的做法就是将这些文本中词语，映射到向量空间，形成文本中文字和向量数据的映射关系，通过计算几个或者多个不同的向量的差异的大小，来计算文本的相似度。下面介绍一个详细成熟的向量空间余弦相似度方法计算相似度。

向量空间余弦相似度(Cosine Similarity)

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，这就叫"余弦相似性"。

                               

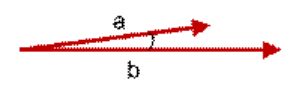
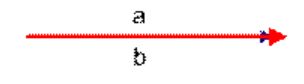
上图两个向量a,b的夹角很小可以说a向量和b向量有很高的的相似性，极端情况下，a和b向量完全重合。如下图：

                              

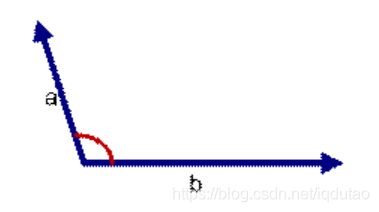
如上图二：可以认为a和b向量是相等的，也即a，b向量代表的文本是完全相似的，或者说是相等的。如果a和b向量夹角较大，或者反方向。如下图

                           

如上图三: 两个向量a，b的夹角很大可以说a向量和b向量有很底的的相似性，或者说a和b向量代表的文本基本不相似。夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。

                                

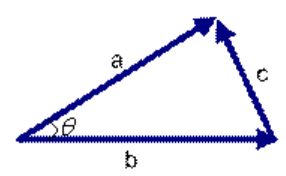
三角形中边a和b的夹角 的余弦计算公式为：

                           

二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

                         

              

即两个n维样本点A(x11,x12,…,x1n)和B(x21,x22,…,x2n)的夹角余弦为：

                                  

                                         

即：

                        

       从数学上看，余弦相似度衡量的是投射到一个多维空间中的两个向量之间的夹角的余弦。当在多维空间中绘制余弦相似度时，余弦相似度体现的是每个向量的方向关系（角度），而非幅度。如果你想要幅度，则应计算欧几里德距离。直观来说，欧几里得距离衡量空间点的直线距离，余弦距离衡量点在空间的方向差异。

余弦相似度很有优势，因为即使两个相似的文件由于大小而在欧几里德距离上相距甚远（比如文档中出现很多次的某个词或多次观看过同一部电影的某用户），它们之间也可能具有更小的夹角。夹角越小，则相似度越高。

余弦相似度Python代码实现

import numpy as np

vec1 = np.array([1, 3, 4])
vec2 = np.array([4, 2, 4])

d = np.dot(vec1,vec2)/(np.linalg.norm(vec1)*(np.linalg.norm(vec2)))

举一个例子来说明，用上述理论计算文本的相似性。为了简单起见，先从句子着手。

句子A：这只皮靴号码大了。那只号码合适

句子B：这只皮靴号码不小，那只更合适

怎样计算上面两句话的相似程度？

基本思路是：如果这两句话的用词越相似，它们的内容就应该越相似。因此，可以从词频入手，计算它们的相似程度。

第一步，分词。

句子A：这只/皮靴/号码/大了。那只/号码/合适。

句子B：这只/皮靴/号码/不/小，那只/更/合适。

第二步，列出所有的词。

这只，皮靴，号码，大了。那只，合适，不，小，很

第三步，计算词频。

句子A：这只1，皮靴1，号码2，大了1。那只1，合适1，不0，小0，更0

句子B：这只1，皮靴1，号码1，大了0。那只1，合适1，不1，小1，更1

第四步，写出词频向量。

句子A：(1，1，2，1，1，1，0，0，0)

句子B：(1，1，1，0，1，1，1，1，1)

到这里，问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段，都是从原点（[0, 0, ...]）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

计算两个句子向量

句子A：(1，1，2，1，1，1，0，0，0)

句子B：(1，1，1，0，1，1，1，1，1)

向量余弦值来确定两个句子的相似度，计算过程如下：

计算结果中夹角的余弦值为0.81非常接近于1，所以，上面的句子A和句子B是基本相似的

由此，我们就得到了文本相似度计算的处理流程是:

（1）找出两篇文章的关键词；

（2）每篇文章各取出若干个关键词，合并成一个集合，计算每篇文章对于这个集合中的词的词频

（3）生成两篇文章各自的词频向量；

（4）计算两个向量的余弦相似度，值越大就表示越相似。
 

8. 汉明距离(Hamming Distance)

定义：两个等长字符串s1与s2的汉明距离为：将其中一个变为另外一个所需要作的最小字符替换次数。例如:

The Hamming distance between "1011101" and "1001001" is 
The Hamming distance between "2143896" and "2233796" is 3. 
The Hamming distance between "toned" and "roses" is 3.

汉明重量：是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4。因此，如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。

应用：汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中，为了增强容错性，应使得编码间的最小汉明距离尽可能大。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。

汉明距离Python代码实现

import numpy as np

vec1 = np.array([1, 1, 0, 1, 0, 1, 0, 0, 1])
vec2 = np.array([0, 1, 1, 0, 0, 0, 1, 1, 1])

d = len(np.nonzero(vec1-vec2)[0])
# 或者
d = np.shape(np.nonzero(vec1-vec2)[0])[0]

 

9. 皮尔森相关系数（Pearson Correlation）

皮尔森相关系数（Pearson correlation coefficient）也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ，是一种线性相关系数，皮尔森相关系数是用来反映两个变量线性相关程度的统计量。考察两个变量的相关关系，首先得看清楚两个变量都是什么类型的，统计分析中常见的变量类型有连续型数值变量，无序分类变量、有序分类变量：

连续型数值变量：如销售额、气温、工资收入、考试成绩；

无序分类变量：如性别男和女，血型种类；

有序分类变量：如学历水平小学、初中、高中、大学、研究生；

适用范围

当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：

(1)两个变量之间是线性关系，都是连续数据。

(2)两个变量的总体是正态分布，或接近正态的单峰分布。

(3)两个变量的观测值是成对的，每对观测值之间相互独立。

相关系数用r表示，其中n为样本量，分别为两个变量的观测值和均值，r描述的是两个变量间线性相关强弱的程度，r的绝对值越大表明相关性越强，系数的正负号代表正相关还是负相关。如果是0，代表没有相关。数值越接近1，相关性越强。

          

公式如下：

                                        

          

皮尔逊相关系数代码实现

def pearson(vector1, vector2):
    n = len(vector1)
    #simple sums
    sum1 = sum(float(vector1[i]) for i in range(n))
    sum2 = sum(float(vector2[i]) for i in range(n))
    #sum up the squares
    sum1_pow = sum([pow(v, 2.0) for v in vector1])
    sum2_pow = sum([pow(v, 2.0) for v in vector2])
    #sum up the products
    p_sum = sum([vector1[i]*vector2[i] for i in range(n)])
    #分子num，分母den
    num = p_sum - (sum1*sum2/n)
    den = math.sqrt((sum1_pow-pow(sum1, 2)/n)*(sum2_pow-pow(sum2, 2)/n))
    if den == 0:
        return 0.0
    return num/den

vector1 = [2,7,18,88,157，90,177,570]

vector2 = [3,5,15,90,180, 88,160,580]

运行结果为0.998，可见这两组数是高度正相关的。

此外，从上面的公式我们知道，皮尔森相关性系数是协方差与标准差的比值，所以它对数据是有比较高的要求的：

第一， 实验数据通常假设是成对的来自于正态分布的总体。为啥通常会假设为正态分布呢？因为我们在求皮尔森相关性系数以后，通常还会用t检验之类的方法来进行皮尔森相关性系数检验，而 t检验是基于数据呈正态分布的假设的。

第二， 实验数据之间的差距不能太大，或者说皮尔森相关性系数受异常值的影响比较大。例如心跳与跑步的例子，万一这个人的心脏不太好，跑到一定速度后承受不了，突发心脏病，那这时候我们会测到一个偏离正常值的心跳（过快或者过慢，甚至为0），如果我们把这个值也放进去进行相关性分析，它的存在会大大干扰计算的结果的。

 

10. 杰卡德距离(Jaccard Distance)

杰卡德距离用于比较有限样本集之间的相似性与差异性

杰卡德相似系数计算公式

杰卡德距离计算公式

 

• 比较文本相似度，用于文本查重与去重；
• 计算对象间距离，用于数据聚类或衡量两个集合的区分度等。

杰拉德距离Python代码实现

import numpy as np
import scipy.spatial.distance as dist

vec1 = np.array([1, 1, 0, 1, 0, 1, 0, 0, 1])
vec2 = np.array([0, 1, 1, 0, 0, 0, 1, 1, 1])

d = dist.pdist(np.array([vec1, vec2]), "jaccard")

 

 

参考链接：https://blog.csdn.net/ruthywei/article/details/82527400

参考链接：https://blog.csdn.net/u012160689/article/details/15341303

参考链接：https://blog.csdn.net/bluesliuf/article/details/88862918

参考链接：https://blog.csdn.net/hustqb/article/details/90290232

参考链接：https://www.jianshu.com/p/5706a108a0c6

参考链接：https://www.cnblogs.com/Zhouwl/p/9482874.html

参考链接：https://blog.csdn.net/abc13526222160/article/details/84073591

参考链接：https://my.oschina.net/hunglish/blog/787596

参考链接：https://blog.csdn.net/u010910642/article/details/51315517