python八进制转二进制
Python is known for being powerful and easy to use when it comes to math. Both its native capabilities and resourceful libraries like NumPy, Pandas, or Scikit-learn, provide developers with the necessary tools for heavy lifting numbers. But sometimes we need to step outside the decimal world and work with one of the other common number bases.
Python在数学方面功能强大且易于使用。 它的本机功能和资源丰富的库(例如NumPy,Pandas或Scikit-learn)都为开发人员提供了繁重工作的必要工具。 但是有时我们需要走出十进制世界,并使用其他常见的数字基数之一。
A number base is the number of digits that a system of counting uses to represent numerical values. The most prevalent number system is the decimal system, also known as base 10. In decimal, the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 represent every possible value. But computers and software developers often need to use other bases.
数字基数是计数系统用来表示数值的位数。 最普遍的数字系统是十进制,也称为基数10。在十进制中,数字0、1、2、3、4、5、6、7、8和9表示每个可能的值。 但是计算机和软件开发人员经常需要使用其他基础。
Of all its cousins, the decimal system invites binary, hexadecimal, and octal over for dinner the most. The others fall into that special category of cousin you avoid when you’re with friends. However, if you plan on using binary, hexadecimal, or octal you may need to brush up on your Python. They are not as clean and easy to use in Python as base 10.
在所有表亲中,十进制系统最多邀请二进制,十六进制和八进制作为晚餐。 其他人属于表亲的特殊类别,与朋友在一起时避免使用。 但是,如果计划使用二进制,十六进制或八进制,则可能需要重新使用Python。 在Python中,它们不如base 10干净,易于使用。
二元 (Binary)
Binary only uses the digits 0 and 1. From these two, it can account for every possible value, the same a the decimal system. Do you remember place values from grade school? That’s exactly how it works. In decimal, every place increases by a multiple of ten, but in binary, every position increases by a multiple of two.
二进制仅使用数字0和1。从这两个数字中,它可以解释每个可能的值,就像十进制一样。 您还记得小学时的地价吗? 这就是它的工作原理。 以十进制表示时,每个位置均增加十倍,而以二进制表示时,每个位置均以两个倍数增。
Base 10 Place Values with Example Numbers of 10, 100, and 1000 以10、100和1000为例的以10为基的地方值 Base 2 Place Values 以2为基数的值For example, 101 would represent a value of 5.
例如,101表示值为5。
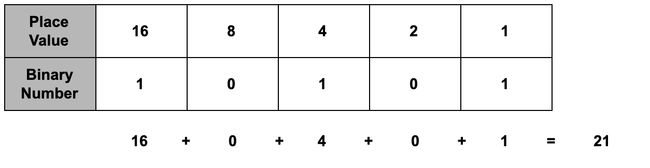
And 10101 would represent a value of 21.
10101代表21。
Ever wonder why your network subnet mask looks something like 255.255.255.0? Because each of those numbers separated by a period is made up of an eight-digit binary number, 11111111.
有没有想过为什么您的网络子网掩码看起来像255.255.255.0? 因为每个数字之间用句点分隔,所以它们由八位二进制数11111111组成。
We could have started this section by stating, “Binary only uses 10 digits.” If you don’t get the joke, read the explanation of how binary works again.
我们可以通过声明“二进制仅使用10位数字”来开始本节。 如果您没有开玩笑,请阅读有关二进制如何再次工作的说明。
In Python, using binary numbers takes a few more steps than using decimal numbers. When you enter a binary number, start with the prefix ‘0b’ (that’s a zero followed by a minuscule b).
在Python中,使用二进制数比使用十进制数要花更多的步骤。 输入二进制数时,请以前缀“ 0b”开头(即为零,后接小数b)。
0b11is the same as binary 11, which equates to a decimal 3. It’s not hard, but it is extra work. Whenever you want to store a binary value in a variable, it will convert it to decimal for you.
0b11与二进制11相同,等同于十进制3。这并不难,但是这是额外的工作。 每当您要将二进制值存储在变量中时,它将为您将其转换为十进制。
number1 = 0b11
number1 = 0b11
This results in the variable number1 storing a value of three. It just stores the value without indicating you’d like it represented in binary. So, when you retrieve it, you’ll get a decimal value of 3. Truthfully, Python processes all the mathematical operators independent of base, but it always returns them to you in decimal.
这导致变量number1存储值为3。 它只是存储值,而没有表明您希望用二进制表示。 因此,当您检索它时,将得到一个十进制值3。实际上,Python处理所有与基数无关的数学运算符,但始终以十进制返回它们。
“But what if I want to have my numbers returned to me in binary?”
“但是如果我想将我的数字以二进制形式返回给我怎么办?”
Glad you asked.
很高兴你问。
If you’d like to keep numbers in your code strictly binary, here’s a solution.
如果您想将代码中的数字严格保留为二进制,这是一种解决方案。
>>> num1 = "0b100"
>>> num2 = "0b110"
>>> mysum = int(num1, 2) + int(num2, 2)
>>> print(bin(mysum))
0b1010In the code snippet above, we started by assigning a string of “0b100” to the variable num1. Next, we assigned a string of “0b110” to the variable num2. So we have two variables of type string storing the binary representation of 4 and 6, respectively.
在上面的代码片段中,我们首先为变量num1分配了字符串“ 0b100”。 接下来,我们将字符串“ 0b110”分配给变量num2 。 因此,我们有两个类型为string的变量,分别存储4和6的二进制表示形式。
Next, we added the two numbers. But as we did that, we converted each to an integer in base 10 using the function int(). Normally int() would throw an error given a string with a letter in it. By specifying the second parameter of 2, we instruct int() to interpret the string as a binary number. So, it stays happy.
接下来,我们将两个数字相加。 但是这样做时,我们使用函数int()将每个都转换为以10为底的整数。 通常,给定一个带有字母的字符串,int()会抛出错误。 通过指定第二个参数2,我们指示int()将字符串解释为二进制数。 因此,它保持快乐。
You can use the second parameter to specify any base between 2 and 36. Bases 2 and 36 are included in the range.
您可以使用第二个参数指定2到36之间的任何底数。范围中包括2到36的底数。
After we add the two numbers together and store the result in mysum, we print the sum. But it’s been stored independent of base. When we recall it, it still wants to present it to us in decimal. So we must tell Python we want our number in binary. Using the bin() function converts the value to binary before it’s printed to the screen.
将两个数字相加并将结果存储在mysum ,我们将打印出总和。 但它的存储独立于基础。 当我们回想起它时,它仍然想以十进制形式将其呈现给我们。 所以我们必须告诉Python我们想要二进制数。 使用bin()函数可在将值打印到屏幕之前将其转换为二进制。
The above code gives you a clear representation of binary in Python. However, you may also use a more abbreviated version, like this.
上面的代码为您提供了Python中二进制的清晰表示。 但是,您也可以使用这样的缩写形式。
>>> num1 = 0b100
>>> num2 = 0b110
>>> mysum = num1 + num2
>>> print(bin(mysum))You get the same result. The sole difference is how you are storing the numbers in variables num1 and num2. If you print either variable to the screen in the first example, you will see it in binary even though it’s technically a string. In the second example, you will see a decimal unless you use bin() to convert it.
您得到相同的结果。 唯一的区别是如何将数字存储在变量num1和num2 。 如果在第一个示例中将任何一个变量打印到屏幕上,即使从技术上讲它是一个字符串,您都将以二进制形式看到它。 在第二个示例中,除非使用bin()进行转换,否则将看到一个小数。
>>> num1 = "0b100"
>>> print(num1)
"0b100">>> num1 = 0b100
>>> print(num1)
4
>>> print(bin(num1))
0b100十六进制 (Hexadecimal)
Decimal uses ten digits, binary uses two digits, and hexadecimal uses sixteen digits. Since we only have the ten digits from the decimal system to use, we substitute letters for everything above the number nine. Therefore, the digits in hexadecimal are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F. They represent zero through nine, then A is worth ten, B is worth eleven, C is worth twelve, D is worth thirteen, E is fourteen, and F wraps up with a value of fifteen. So, there are sixteen digits in hexadecimal. If you write that in hexadecimal, you can state, “Hexadecimal has 10 digits.”
十进制使用十位数字,二进制使用两位数字,十六进制使用十六位数字。 由于我们只能使用十进制的十位数字,因此我们用字母代替数字9以外的所有内容。 因此,十六进制数字为0、1、2、3、4、5、6、7、8、9,A,B,C,D,E和F。它们表示从零到九,则A值得十,B值十一,C值十二,D值十三,E值十四,F值十五。 因此,十六进制有十六位数字。 如果用十六进制写,则可以说:“十六进制有10位数字。”
Wait? Haven’t we seen that before? Yes. Honestly, a ‘10’ always represents the total number of digits in any base if you are writing the number in the respective number system. But it’s only funny in binary.
等待? 我们以前没看过吗? 是。 老实说,如果您在相应的数字系统中写入数字,则“ 10”始终代表任何基数的总位数。 但这只是二进制形式的有趣。
When denoting hexadecimal numbers in Python, prefix the numbers with ‘0x’. Also, use the hex() function to convert values to hexadecimal format for display purposes.
在Python中表示十六进制数字时,请在数字前加上“ 0x”。 同样,使用hex()函数将值转换为十六进制格式以用于显示。
Our two hexadecimal code samples are similar to the ones we used for binary.
我们的两个十六进制代码样本类似于我们用于二进制的样本。
>>> hnum1 = "0x10"
>>> hnum2 = "0x10"
>>> myhsum = int(hnum1, 16) + int(hnum2, 16)
>>> print(hnum1)
"0x10"
>>> print(myhsum)
32
>>> print(hex(myhsum))
0x20>>> hnum1 = 0x10
>>> hnum2 = 0x10
>>> myhsum = hnum1 + hnum2
>>> print(hnum1)
16
>>> print(myhsum))
32
>>> print(hex(myhsum))
0x20八进制 (Octal)
Finally, the same holds for octal. Any guesses on how many digits are in the octal number system? Octal stands for eight. Right, octal contains eight digits. And instead of bin() or hex(), we use oct() to convert numbers to octal in Python. We prefix octal numbers with a zero followed by a lowercase o, like ‘0o’.
最后,八进制也是如此。 关于八进制数字中有多少位数的任何猜测? 八进制代表八。 对,八进制包含八位数字。 而不是bin()或hex(),我们使用oct()在Python中将数字转换为八进制。 我们在八进制数字前加一个零,后跟一个小写的o,例如“ 0o”。
The eight digits of octal are 0, 1, 2, 3, 4, 5, 6, 7.
八进制的八位数字是0、1、2、3、4、5、6、7。
Let’s use the same code sample here, but we’ll use the proper notation and conversion function for octal.
让我们在这里使用相同的代码示例,但对八进制使用正确的符号和转换函数。
>>> onum1 = "0o10"
>>> onum2 = "0o10"
>>> myosum = int(onum1, 8) + int(onum2, 8)
>>> print(onum1)
"0o10"
>>> print(myosum)
16
>>> print(oct(myosum))
0o20>>> onum1 = 0o10
>>> onum2 = 0o10
>>> myosum = onum1 + onum2
>>> print(onum1)
8
>>> print(myosum))
16
>>> print(oct(myosum))
0o20结论 (Conclusion)
The great thing about Python is it can do nearly everything except my laundry. And I’m working on that.
关于Python的伟大之处在于,它几乎可以完成除洗衣之外的所有工作。 我正在努力。
The takeaways are simple:
外卖很简单:
- Binary uses bin() and ‘0b’. 二进制使用bin()和'0b'。
- Hexadecimal uses hex() and ‘0x’. 十六进制使用hex()和'0x'。
- Octal uses oct() and ‘0o’. 八进制使用oct()和'0o'。
The int() function can be used to convert numbers into a base 10 integer from any base between 2 and 36 by changing the second parameter. e.g. int(number, 30)
通过更改第二个参数,可以使用int()函数将数字从2到36之间的任何底数转换为以10为底的整数。 例如int(number,30)
Even though using bases outside our beloved decimal system requires a bit more effort, Python easily adapts and empowers us to go where no decimal has gone before — into the final frontier of other bases.
即使在我们钟爱的十进制系统之外使用基数需要付出更多的努力,Python仍可以轻松地进行调整,使我们能够走到以前没有十进制的地方-进入其他基数的最终领域。
Rod Castor helps companies Get Analytics Right! He helps international organizations and small businesses improve their data analytics, data science, tech strategy, and tech leadership efforts. In addition to consulting, Rod also enjoys public speaking, teaching, and writing. You can discover more about Rod and his work at rodcastor.com and through his mailing list.
Rod Castor帮助公司正确完成分析! 他帮助国际组织和小型企业改善数据分析,数据科学,技术战略和技术领导力。 除了提供咨询服务外,Rod还喜欢公开演讲,教学和写作。 您可以在rodcastor.com和他的邮件列表中找到有关Rod及其工作的更多信息。
翻译自: https://towardsdatascience.com/binary-hex-and-octal-in-python-20222488cee1
python八进制转二进制