简单的排序算法思想
简单的排序思想
- 插入排序
-
- 直接插入排序
-
- 从前往后的直接插入排序
- 从后往前的直接插入排序(交换)
- 从后往前的直接插入排序(不交换)
- 从后往前的直接插入排序(*具有哨兵位)
- 折半插入法
- 二路插入法
- 希尔排序
- 选择排序
- 堆排序
- 冒泡排序
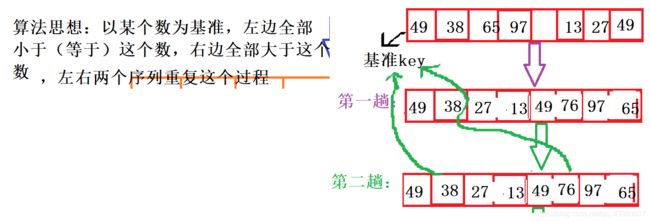
- 快速排序**(递归)
- 归并排序
-
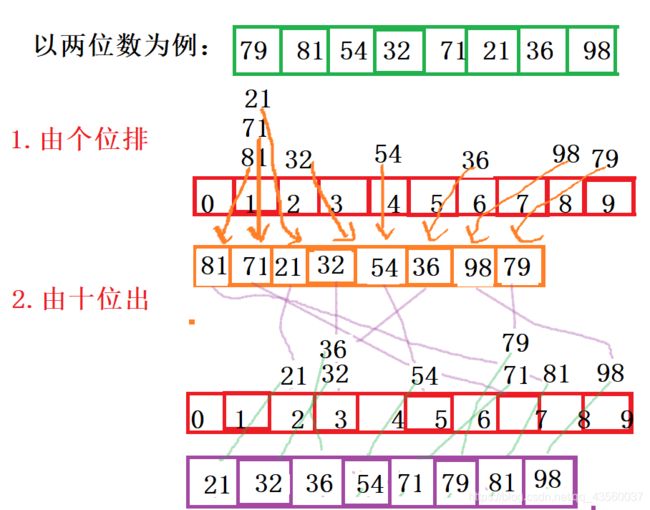
- 基数排序(非比较排序)
- 算法效率
插入排序
直接插入排序
从前往后的直接插入排序
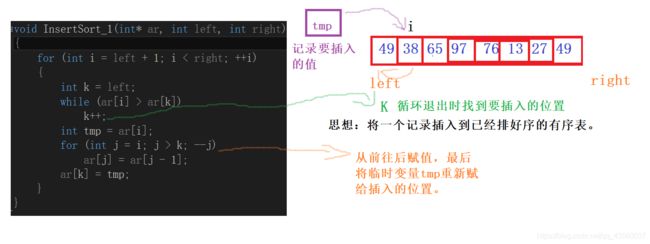
首先解释一下为什么传参选择left和right而不是数组元素个数n,这样做可以更加灵活的排序,比如你可以指定数组内第3个元素到第6个元素排序,而其他元素不排序
void InsertSort_1(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
int k = left;
while (ar[i] > ar[k])
k++;
int tmp = ar[i];
for (int j = i; j > k; --j)
ar[j] = ar[j - 1];
ar[k] = tmp;
}
}
缺点,当要排序的数字比前面排好序的数字都大时,仍然需要从头开始循环来找位置,时间效率减小。
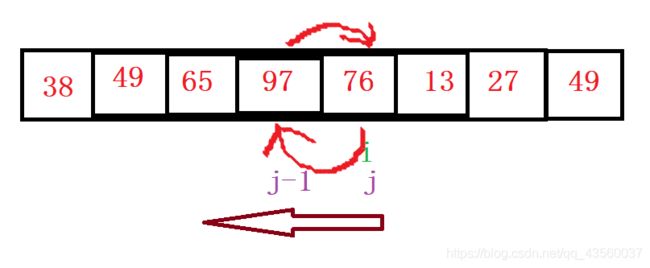
从后往前的直接插入排序(交换)
交换函数(传址调用)
void Swap(int* a, int* b)//交换
{
int tmp = *a;
*a = *b;
*b = tmp;
}
void InsertSort_2(int* ar, int left, int right)
{
for (int i = left+1; i < right; ++i)
{
int j = i;
while (j > left && ar[j] < ar[j - 1])//j>left是为了防止越界访问
{
Swap(&ar[j], &ar[j - 1]);
j--;
}
}
}
此方法有效杜绝了从前往后排序的弊端,但是会频繁调用外部交换函数,时间效率很低。
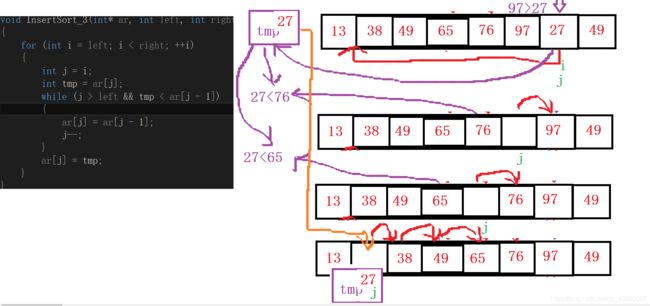
从后往前的直接插入排序(不交换)
void InsertSort_3(int* ar, int left, int right)
{
for (int i = left; i < right; ++i)
{
int j = i;
int tmp = ar[j];
while (j > left && tmp < ar[j - 1])
{
ar[j] = ar[j - 1];
j--;
}
ar[j] = tmp;
}
}
此方法有效避免使用交换函数,效率相比上面两个方法时间效率提高。
从后往前的直接插入排序(*具有哨兵位)
哨兵位设置是为了避免数组越界操作,需要多留出一个辅助空间,即省略了上述代码判断条件中“j
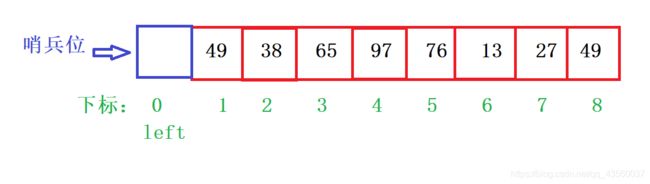
void InsertSort_4(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
ar[0] = ar[i];
int j = i;
while (ar[0] < ar[j - 1])//省略了j>left;
{
ar[j] = ar[j - 1];
j--;
}
ar[j] = ar[0];
}
}
需要注意的是,使用该算法时传参left在主函数中已经不是上述其他几种算法中的left,而应该是“left+1”。
折半插入法
算法思想依然是在有序的数组中查找插入位置并插入,而“查找”这一步使用二分查找法。
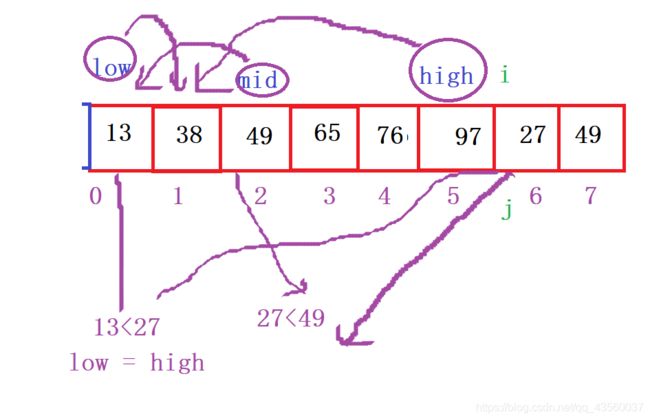
void BinInsertSort(int* ar, int left, int right)
{
for (int i = left + 1; i < right; ++i)
{
int tmp = ar[i];
int low = left;
int high = i - 1;
int mid;
while (low <= high)
{
mid = (low + high) / 2;
if (tmp >= ar[mid])
low = mid + 1;
if (tmp < ar[mid])
high = mid - 1;
}
for (int j = i; j>low; --j)
{
ar[j] = ar[j - 1];
}
ar[low] = tmp;
}
}
时间效率相比上面几种方法得到了提高
二路插入法
在折半插入算法上改进优化,目的是为了减少排序过程中移动的次数,因此需要n个记录的辅助空间
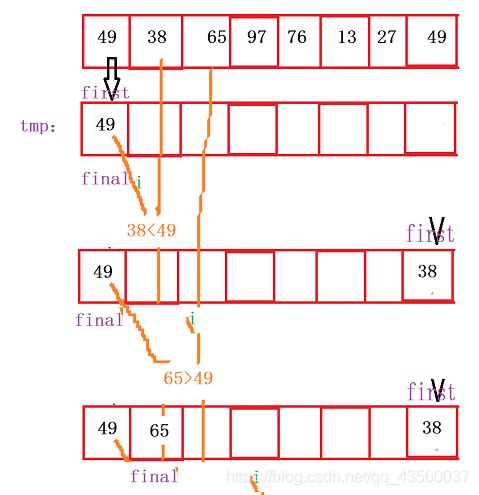
void TwoWayInsertSort(int* ar, int left, int right)
{
int n = right - left;
int* tmp = (int *)malloc(sizeof(int)* n);
tmp[0] = ar[left];
int first, final;
first = final = 0;
for (int i = left + 1; i < right; i++)
{
if (ar[i] < tmp[first])
{
first = (first - 1 + n) % n;
tmp[first] = ar[i];
}
else if (ar[i] >= tmp[final])
{
tmp[++final] = ar[i];
}
else
{
int end = final;
while (ar[i] < tmp[end])
{
tmp[(end + 1)%n] = tmp[end];//取模值是为了防止越界
end = (end-1+n)%n;
}
tmp[(end + 1)%n] = ar[i];
final++;
}
}
int k = 0;
for (int i = first; k < n; ++k)//拷贝回去
{
ar[k] = tmp[i];
i = (i + 1) % n;
}
free(tmp);
tmp = NULL;
}
该方法将数组访问设置成循环模式,当要插入的值为最小值时可直接插入而不需要往后挪。
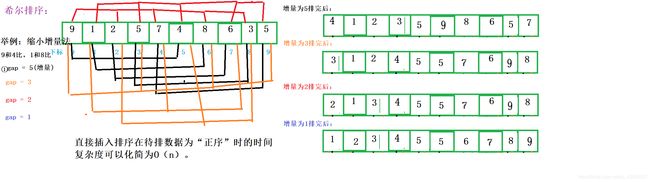
希尔排序
void ShellSort(int* ar, int left, int right)
{
int gap = right - left;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = left + gap; i < right; ++i)
{
if (ar[i] < ar[i - gap])
{
int tmp = ar[i];
int j = i;
while (j>left && tmp < ar[j - gap])
{
ar[j] = ar[j - gap];
j -= gap;
}
ar[j] = tmp;
}
}
}
}
时间效率相比之前算法大幅度提高
选择排序
将第一个数看做最小的,然后通过比较将较小值与第一个数交换
int GetMinIndex(int* ar, int left, int right)//获取最小下标
{
int min_value = ar[left];
int index = left;
for (int i = left + 1; i < right; ++i)
{
if (ar[i] < min_value)
{
min_value = ar[i];
index = i;
}
}
return index;
}
void SelectSort(int* ar, int left, int right)
{
for (int i = left; i < right - 1; ++i)
{
int index = GetMinIndex(ar, i, right);
if (index != i)
Swap(&ar[i], &ar[index]);
}
}
是一种比较中庸的排序算法
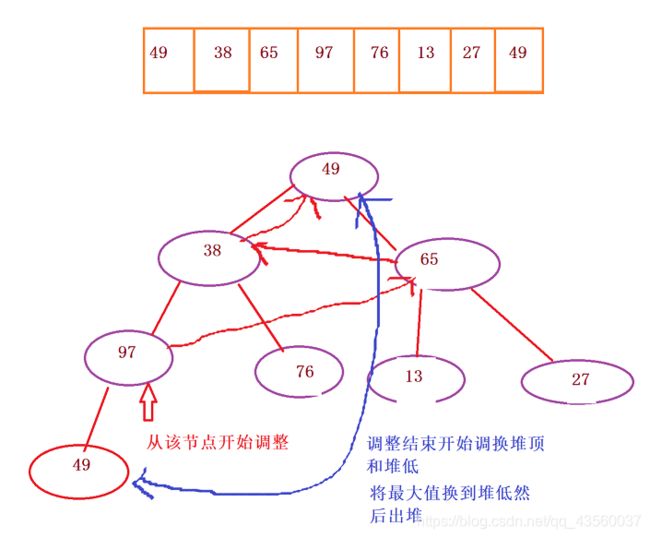
堆排序
void AdjustDown(int* ar, int left, int right, int start)//赋值法向下调整
{
int n = right - left;
int i = start;
int j = 2*i + 1;
int tmp = ar[i];
while (j < n)
{
if (j + 1 < n && ar[j] < ar[j + 1])//右树存在且左树大于右数
j = j + 1;
if (tmp < ar[j])
{
ar[i] = ar[j];//满足条件向上赋值
i = j;
j = i * 2 + 1;
}
else
break;
}
ar[i] = tmp;
}
void HeapSort(int* ar, int left, int right)
{
int n = right - left;
int curpos = n / 2 - 1 + left;//找到最后一个分支
while (curpos >= 0)
{
AdjustDown(ar, left, right, curpos);
curpos--;
}
//将顶与低交换
int end = right - 1;
while (end > left)
{
Swap(&ar[left], &ar[end]);//出堆
AdjustDown(ar, left, end, 0);
end--;
}
}
堆排序的算法思想基于二叉树遍历,所以时间效率很高
冒泡排序
void BubbleSort_1(int* ar, int left, int right)
{
bool flag = false;
for (int i = left; i < right - left - 1; ++i)
{
for (int j = left; j < right - left - 1 - i; ++j)
{
if (ar[j] > ar[j + 1])
{
Swap(&ar[j], &ar[j + 1]);
flag = true;
}
}
if (!flag)
break;
else
flag = false;
}
}
加上flag可避免不必要的比较
快速排序**(递归)
int _Partition_1(int* ar, int left, int right)//hoare法
{
int low = left, high = right - 1;
int key = ar[low];
while (low < high)
{
while (low < high && ar[high] > key)
high--;
Swap(&ar[low], &ar[high]);
while (low < high && ar[low] <= key)
low++;
Swap(&ar[low], &ar[high]);
}
return low;
}
int _Partition_2(int* ar, int left, int right)//挖坑法
{
int low = left, high = right - 1;
int key = ar[low];
while (low < high)
{
while (low < high && ar[high] > key)
high--;
ar[low] = ar[high];
while (low < high && ar[low] <= key)
low++;
ar[high] = ar[low];
}
ar[low] = key;
return low;
}
int _Partition_3(int* ar, int left, int right)//前后指针法
{
int key = ar[left];
int pos = left;
for (int i = pos + 1; i < right; ++i)
{
if (ar[i] < key)
{
pos++;
if (pos != i)
{
Swap(&ar[pos], &ar[i]);
}
}
}
Swap(&ar[left], &ar[pos]);
return pos;
}
void QuickSort(int* ar, int left, int right)
{
if (left >= right)
return;
int pos = _Partition_3(ar, left, right);
QuickSort(ar, left, pos);//左子序列
QuickSort(ar, pos + 1, right);//右子序列
}
最常用的高效排序算法
归并排序
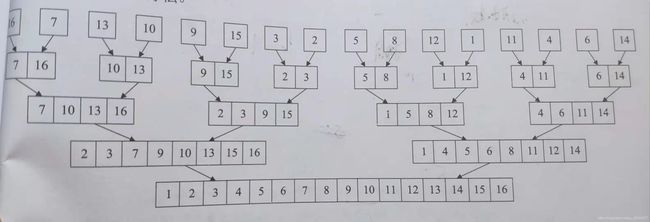
归并排序算法思想:将n个记录看成n个子序列,每个子序列长度为1,两两归并得到长度为2的有序子序列,循环进行,直到长度为n
void _MergeSort(int* ar, int left, int right,int* tmp)
{
if (left >= right)
return;
int mid = (left + right) / 2;
_MergeSort(ar, left, mid, tmp);//分解左边分支
_MergeSort(ar, mid + 1, right, tmp);//分解右边分支
归并
int begin1, end1, begin2, end2;
begin1 = left, end1 = mid;
begin2 = mid + 1, end2 = right;
int k = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (ar[begin1] < ar[begin2])
tmp[k++] = ar[begin1++];
else
tmp[k++] = ar[begin2++];
}
while (begin1 <= end1)
tmp[k++] = ar[begin1++];
while (begin2 <= end2)
tmp[k++] = ar[begin2++];
memcpy(ar + left, tmp + left, sizeof(int)* (right - left + 1));
}
void MergeSort(int* ar, int left, int right)
{
int n = right - left;
int * tmp = (int*)malloc(sizeof(int)* n);
_MergeSort(ar, left, right-1,tmp);
free(tmp);
}
稳定排序且效率高
基数排序(非比较排序)
算法效率
void TestSortEfficient()
{
int n = 20000;
int* a = (int*)malloc(sizeof(int)*n);
int* a1 = (int*)malloc(sizeof(int)*n);
int* a2 = (int*)malloc(sizeof(int)*n);
int* a3 = (int*)malloc(sizeof(int)*n);
int* a4 = (int*)malloc(sizeof(int)*n);
int* a5 = (int*)malloc(sizeof(int)*n);
int* a6 = (int*)malloc(sizeof(int)*n);
int* a7 = (int*)malloc(sizeof(int)*n);
int* a8 = (int*)malloc(sizeof(int)*n);
int* a9 = (int*)malloc(sizeof(int)*n);
int* a10 = (int*)malloc(sizeof(int)*n);
int* a11 = (int*)malloc(sizeof(int)*n);
int* a12 = (int*)malloc(sizeof(int)*n);
int* a13 = (int*)malloc(sizeof(int)*n);
int* a14 = (int*)malloc(sizeof(int)*n);
srand(time(0));
for (int i = 0; i < n; ++i)
{
a[i] = rand();
a1[i] = a[i];
a2[i] = a[i];
a3[i] = a[i];
a4[i] = a[i];
a5[i] = a[i];
a6[i] = a[i];
a7[i] = a[i];
a8[i] = a[i];
a9[i] = a[i];
a10[i] = a[i];
a11[i] = a[i];
a12[i] = a[i];
a13[i] = a[i];
a14[i] = a[i];
}
time_t start = clock();
InsertSort_1(a, 0, n);
time_t end = clock();
printf("InsertSort_1 time = %u\n", end - start);
start = clock();
InsertSort_2(a1, 0, n);
end = clock();
printf("InsertSort_2 time = %u\n", end - start);
start = clock();
InsertSort_3(a2, 0, n);
end = clock();
printf("InsertSort_3 time = %u\n", end - start);
start = clock();
InsertSort_4(a3, 0, n);
end = clock();
printf("InsertSort_4 time = %u\n", end - start);
start = clock();
BinInsertSort(a4, 0, n);
end = clock();
printf("BinInsertSort time = %u\n", end - start);
start = clock();
TwoWayInsertSort(a5, 0, n);
end = clock();
printf("TwoWayInsertSort time = %u\n", end - start);
start = clock();
ShellSort(a6, 0, n);
end = clock();
printf("ShellSort time = %u\n", end - start);
start = clock();
SelectSort(a7, 0, n);
end = clock();
printf("SelectSort time = %u\n", end - start);
start = clock();
HeapSort(a8, 0, n);
end = clock();
printf("HeapSort time = %u\n", end - start);
start = clock();
BubbleSort(a9, 0, n);
end = clock();
printf("BubbleSort time = %u\n", end - start);
start = clock();
BubbleSort_1(a10, 0, n);
end = clock();
printf("BubbleSort_1 time = %u\n", end - start);
start = clock();
QuickSort(a11, 0, n);
end = clock();
printf("QuickSort time = %u\n", end - start);
start = clock();
QuickSort_1(a12, 0, n);
end = clock();
printf("QuickSort_1 time = %u\n", end - start);
start = clock();
MergeSort(a13, 0, n);
end = clock();
printf("MergeSort time = %u\n", end - start);
start = clock();
RadixSort(a14, 0, n);
end = clock();
printf("RadixSort time = %u\n", end - start);
}
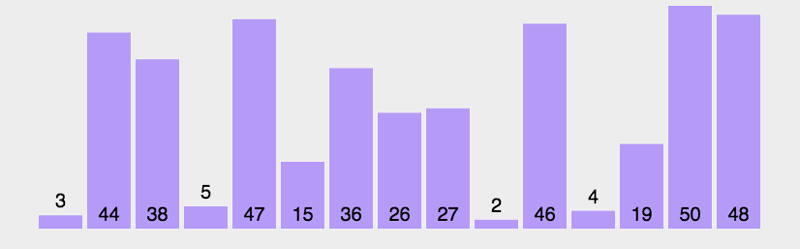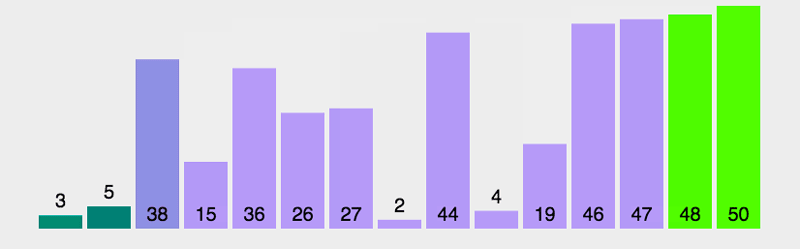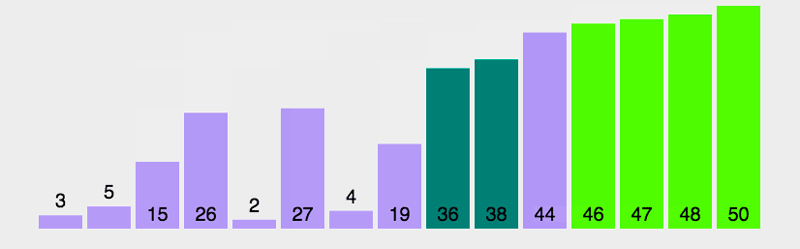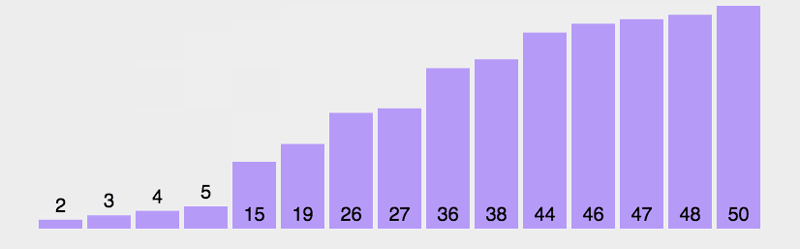
得出结果
时间效率如下:
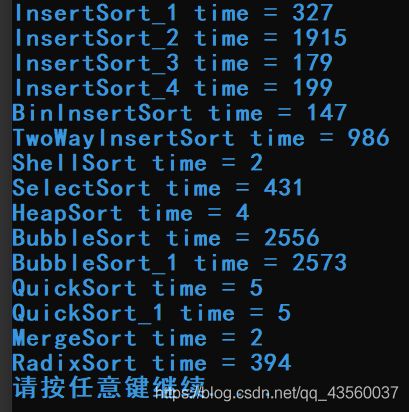
标没有十全十美的排序算法,有优点就有缺点,快速排序性能优越但是不稳定,需要辅助空间,对于少量的数据排序效率不高