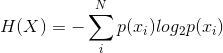分析RGB文件&YUV文件三通道概率密度，并计算信息熵------数据压缩hw2

1 实验目标

对down.rgb和down.yuv分析三个通道的概率分布，并计算各自的熵。

两个文件的分辨率均为256*256，yuv为4:2:0采样空间，存储格式为：rgb文件按每个像素BGR分量依次存放；YUV格式按照全部像素的Y数据块、U数据块和V数据块依次存放。

---

2 实验步骤

2.1 RGB、YUV格式文件存储方式

RGB：

存储方式为依次存储RGB，即B1G1R1B2G2R2......

故该实验文件的存储空间为：256*256*3

参考

YUV：

存储方式为先存储全部Y，再存储全部U，再存储全部V。

故该实验文件的存储空间为：256*256*(1+1/4*2) (U、V各为Y的1/4）

参考

2.2 读取文件

本文采用c++实现，将实验文件读入数组处理。image_rgb与image_yuv两个数组存储原图像。

2.3 计算概率

R,G,B三个数组存储统计0~255不同颜色出现的次数，并在统计完成后计算概率（/size）

Y,U,V在计算概率时注意各自大小不同

2.4 绘制图表

将统计计算得到的数据写入csv文件，再导入excel绘制成可视化图表

2.5 计算熵

3 实验代码

3.1 RGB

#include 
#include 
#include 

using namespace std;

#define size 256*256
#define V_start 81920 //256*256*1.25

int main()
{
    unsigned char* image_rgb;
    unsigned char* image_yuv;
    double R[256] = { 0 }, G[256] = { 0 }, B[256] = { 0 };
    double Y[256] = { 0 }, U[256] = { 0 }, V[256] = { 0 };
    double h_R = 0, h_G = 0, h_B = 0;
    double h_Y = 0, h_U = 0, h_V = 0;
    image_rgb = new unsigned char[size*3];
    image_yuv = new unsigned char[size*1.5];

    //输出文件
    FILE* outR = NULL;
    fopen_s(&outR, "C:\\Users\\11191\\Desktop\\dataconpress\\rstat.csv", "w");
    FILE* outG = NULL;
    fopen_s(&outG, "C:\\Users\\11191\\Desktop\\dataconpress\\gstat.csv", "w");
    FILE* outB = NULL;
    fopen_s(&outB, "C:\\Users\\11191\\Desktop\\dataconpress\\bstat.csv", "w");

    FILE* fin_rgb;
    fopen_s(&fin_rgb, "C:\\Users\\11191\\Desktop\\dataconpress\\down.rgb", "rb");
    fread(image_rgb, sizeof(unsigned char), size * 3, fin_rgb);

    //RGB

    //统计次数
    for (int i = 0; i < size; i++) {
        B[int(image_rgb[i * 3])]++;
        G[int(image_rgb[i * 3 + 1])]++;
        R[int(image_rgb[i * 3 + 2])]++;
    }

    //计算概率
    for (int i = 0; i < 256; i++) {
        R[i] /= size;
        G[i] /= size;
        B[i] /= size;
    }

    //计算熵
    for (int i = 0; i < 256; i++) {
        if (R[i])h_R -= R[i] * log(R[i]) / log(2);
        if (G[i])h_G -= G[i] * log(G[i]) / log(2);
        if (B[i])h_B -= B[i] * log(B[i]) / log(2);
    }
    cout << "H(R)=" << h_R << " H(G)=" << h_G << " H(B)=" << h_B << endl;

    //写入csv
    fprintf(outR, "Symbol,Frequency\n");
    fprintf(outG, "Symbol,Frequency\n");
    fprintf(outB, "Symbol,Frequency\n");

    for (int i = 0; i < 256; i++) {
        fprintf(outR, "%-3d,%-8.2e\n", i, R[i]);
        fprintf(outG, "%-3d,%-8.2e\n", i, G[i]);
        fprintf(outB, "%-3d,%-8.2e\n", i, B[i]);
    }

    return 0；
}

 

3.2 YUV （片段，相同部分略去）

    //YUV
    
    //输出文件
    FILE* outY = NULL;
    fopen_s(&outY, "C:\\Users\\11191\\Desktop\\dataconpress\\ystat.csv", "w");
    FILE* outU = NULL;
    fopen_s(&outU, "C:\\Users\\11191\\Desktop\\dataconpress\\ustat.csv", "w");
    FILE* outV = NULL;
    fopen_s(&outV, "C:\\Users\\11191\\Desktop\\dataconpress\\vstat.csv", "w");

    FILE* fin_yuv;
    fopen_s(&fin_yuv, "C:\\Users\\11191\\Desktop\\dataconpress\\down.yuv", "rb");
    fread(image_yuv, sizeof(unsigned char), size * 1.5, fin_yuv);

    //统计次数
    for (int i = 0; i < size; i++)Y[int(image_yuv[i])]++;
    for (int i = size; i < V_start; i++)U[int(image_yuv[i])]++;
    for (int i = V_start; i < size * 1.5; i++)V[int(image_yuv[i])]++;

    //计算概率
    for (int i = 0; i < 256; i++) {
        Y[i] /= size;
        U[i] /= size/4;
        V[i] /= size/4;
    }

    //计算熵
    for (int i = 0; i < 256; i++) {
        if (Y[i])h_Y -= Y[i] * log(Y[i]) / log(2);
        if (U[i])h_U -= U[i] * log(U[i]) / log(2);
        if (V[i])h_V -= V[i] * log(V[i]) / log(2);
    }
    cout << endl << "H(Y)=" << h_Y << " H(U)=" << h_U << " H(V)=" << h_V << endl;

    //写入csv
    fprintf(outY, "Symbol,Frequency\n");
    fprintf(outU, "Symbol,Frequency\n");
    fprintf(outV, "Symbol,Frequency\n");

    for (int i = 0; i < 256; i++) {
        fprintf(outY, "%-3d,%-8.2e\n", i, Y[i]);
        fprintf(outU, "%-3d,%-8.2e\n", i, U[i]);
        fprintf(outV, "%-3d,%-8.2e\n", i, V[i]);
    }

 

4 实验结果

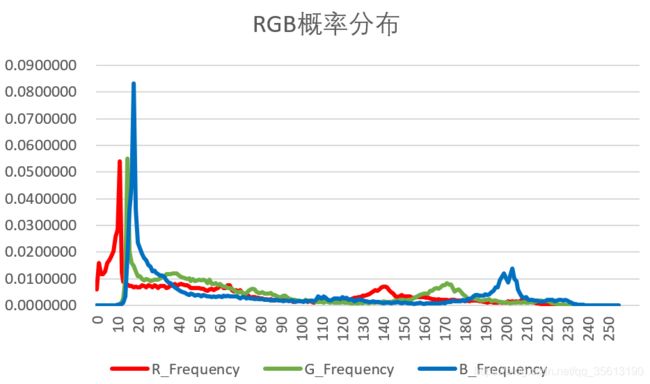
4.1 概率分布

4.2 熵的计算

分量	熵
R	7.22955
G	7.17846
B	6.85686

分量	熵
Y	6.33182
U	5.1264
V	4.11314

5 感想总结

本实验综合性比较强，融合了多方面的知识，主要包括：

1、问题的解析——只有从头到尾对问题全面剖析，将问题拆分为多个小问题，逐个击破，才能较为顺利的解决。否则大概率一头雾水，无从下手。就本实验而言，从问题”概率分布和熵“出发，自然而然将问题导向对图像存储的方式，了解之后才能进行下一步的算法编写。

2、不同文件格式的理解——了解rgb与yuv格式对分量的不同存储方式

3、c++代码的编写——此处问题较多，与问题解析类似，代码的编写也涉及问题的拆分。文件读写方式多样，如何选择并正确使用较为重要（fopen，fread，fprintf函数的运用）；数据的存储与处理；算法的构思：统计0~255出现的次数进而求得概率

4、数据的导出——解决方式多种多样，可能使用python绘图较为方便，但是该方面知识实在是不足。。。

5、可视化数据——本文使用了导出为csv文件格式，并在excel中画图的方式。问题较多，在如何导出为csv格式以及excel绘图上花了较多时间。