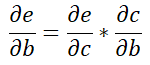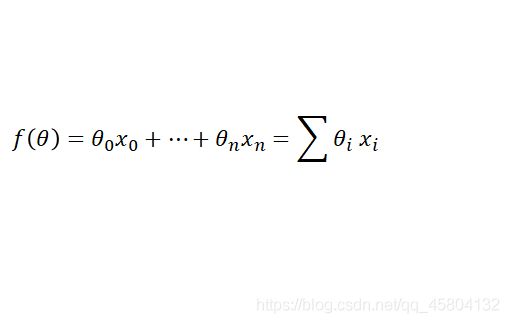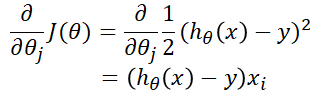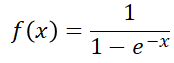反馈神经网络：反向传播算法与简单的反馈神经网络算法python实现，在脱离api的路上越走越远。。。

本文就数学原理，思想基础，python实现几个角度讲解反向传播的实现，需要部分基础，可能跟我差不多的小白会看的有点吃力。。。

---

一. 深度学习基础

1. 深度学习

深度学习是统计学的应用，属于机器学习基础之后的内容。它的任务其实与机器学习殊途同归，都是在寻找数据与数据的关系，结果与影响因素的一一对应关系。就像是寻找x，y的关系，建立一个模型，这里将狭义的x，y拓展到了向量，矩阵，等张量。而随着数据复杂度的增加，也不能在用一个简单的函数，对输入做映射了。
在数学中，通过各种复杂的多元函数，高阶函数解决复杂模型的拟合问题。但是过于复杂的函数式求解本身存在很大的难度，想要获取其公式更是难上加难。
经过前人的研究，发现可以通过神经网络表示这样一个一一对应的关系。而神经网络的本质也就是一个多元复合函数。通过增加网络的层次和神经元，可以更好的表达函数的复合关系。

2. 反向传播算法

众所周知，反向传播算法是神经网络的核心与精髓，好吧，开玩笑。反向传播算法在训练中确实占据了举足轻重的地位。它到底是个什么？
其实反向传播算法并不复杂，就像是，更像是字面意思，反向，传播。它是高数中链式求导法则的一个强大的应用。接下来回讲到一个反向传播算法应用的基础。

3. 梯度下降算法与链式求导法则

梯度下降算法是链式求导法则的一个应用，梯度下降算法属于BP神经网路的经典算法，我们先来说链式求导法则。

①. 链式求导法则

链式求导法则是高数中的一种求导方法。

上图为公式的整个过程，在本例中我们要求得e对各个点的梯度。需要将每个点与e连接起来，比如我们要求e对输入点a的梯度。那么我们需要。

这样我们就将e和b梯度联系起来了。于是通过同理推导，可以得到e对b求偏导。

显然，e对a求偏导就是建立了一条路径，这样就很容易求偏导，这也就是链式求导的强大应用。

②. 梯度向量

梯度向量：

如果将神经网络数学公式按向量的形式去写：

那么梯度向量就是如下：

所谓的梯度向量其实就是求出函数在每个向量的偏导数之和，这也正是链式法则解决的问题了。

③. 梯度下降算法

梯度下降原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快，这也正是梯度下降名字的由来，其原先的故事是道士下山，不过读者们可自己去了解。
从函数的角度来看，对于一个函数J(θ)来说，无非就是求它的偏导。但偏导却不一定负数，因此我们要求的是这个偏导的相反数，视为它的反梯度。其求解过程如下：
这里的J(θ)复合了f(θ)和y

首先我们要定义f(θ):

h本质上是f，只是为了表现出θ将其改写为这种格式。

具体过程建议自己字草稿纸上上推导。

求得梯度之后就可以，用如下公式不断迭代求θ

其中a为学习率，就是代表没每一步固定要走多远，这样的话就很容易想到，如果a设置很大的话，很有可能会走不到局部最小点。从公式来看的话，也容易分析得到，该公式本质是求局部极小点的，这是它的优点，也是它的致命缺点。导致了后来，如果一个函数曲线的极小点过多，那么它的效果很差，因为往往在某个极小点迭代就会停止。产从实际角度来看就是，从山上往下走，走到某个坑，看到对面已经是上坡了，就认为自己已经下山了，殊不知，自己只是在山上的一个坑洞中。

python代码：

x=[(2,0,3),(1,0,3),(1,1,3),(1,4,2),(1,2,4)]
y=[5,6,8,10,11]

epsilon=0.002
alpha=0.002
diff=[0,0]
max_itor=1000
error0=0
error1=0
cnt=0


m=len(x)
theta0=0
theta1=0
theta2=0

while True:
    cnt+=1
    
    for i in range(m):
        diff[0]=(theta0*x[i][0]+theta1*x[i][1]+theta2*x[i][2])-y[i]
        theta0-=alpha*diff[0]*x[i][0]
        theta1-=alpha*diff[0]*x[i][1]
        theta2-=alpha*diff[0]*x[i][2]
        
    error1=0
    for lp in range(len(x)):
        error1+=(y[lp]-(theta0*x[lp][0]+theta1*x[lp][1]+theta2*x[lp][2]))**2/2
    if abs(error1-error0)<epsilon :
        break
    else:
        error0=error1
        
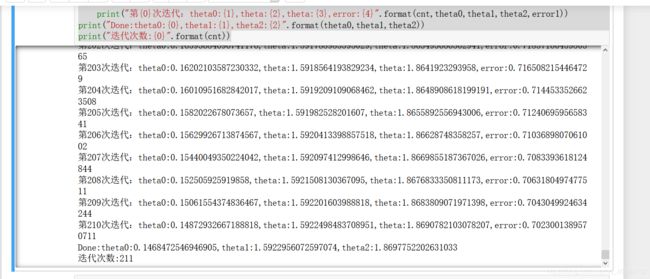
    print("第{0}次迭代：theta0:{1},theta:{2},theta:{3},error:{4}".format(cnt,theta0,theta1,theta2,error1))
print("Done:theta0:{0},theta1:{1},theta2:{2}".format(theta0,theta1,theta2))
print("迭代次数:{0}".format(cnt))

结果如下：

4. 最小二乘法

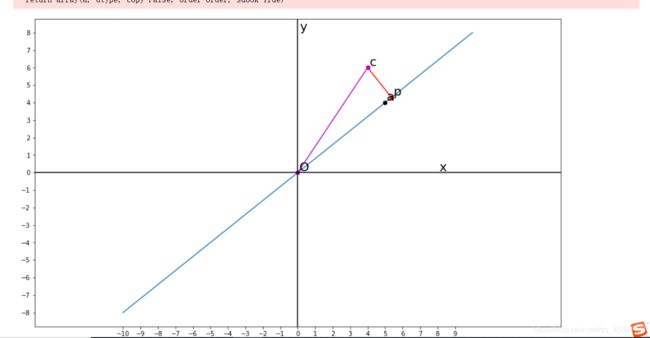
最小二乘法是机器学习的常用算法，它的作用是函数匹配，直观来说如果在二维平面中，它的目的就是在从一堆数据点之中，找到与这些点的距离之后最小的一条直线，显然它具有预测数据的功能。

这里直接应用的是残差，也就是真实值与计算值的差的平方和。表达残差的方式有三种。
范数
L-1范数
L-2范数
这三个数可以自己去了解。
我们只需要知道对于给定的数据，在确定的假设空间中。使得残差δ最小。

对于一元多项式来说，它的目标就是找到一组权重使得，残差最小。其求法就是f对每个权重w求偏导，使偏导为0求出极值点。

代码：

'''
numpy实现最小二乘法
'''
#导库
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (15,9)

a=np.array([[5],[4]],dtype='float32')
c=np.array([[4],[6]],dtype='float32')
#矩阵积
b=np.dot(a.T,c)
#求逆矩阵
aa=np.linalg.inv(a.T.dot(a))
l=aa.dot(b)
print('l',l)
#构造一个线性函数权值为l
p=a.dot(l)
print('p',p)
#获取一个排列的数据
x=np.linspace(-2,2,10)
#调整维度
x.shape=(1,10)
xx=a.dot(x)
fig=plt.figure()
ax=fig.add_subplot(111)
ax.plot(xx[0,:],xx[1,:])
ax.plot(a[0],a[1],'ko')

ax.plot([c[0],p[0]],[c[1],p[1]],'r-o')
ax.plot([0,c[0]],[0,c[1]],'m-o')

ax.axvline(x=0,color='black')
ax.axhline(y=0,color='black')

margin=0.1

ax.text(a[0]+margin,a[1]+margin,r'a',fontsize=20)
ax.text(c[0]+margin,c[1]+margin,r'c',fontsize=20)
ax.text(p[0]+margin,p[1]+margin,r'p',fontsize=20)


ax.text(0+margin,0+margin,r"O",fontsize=20)
ax.text(0+margin,8+margin,r'y',fontsize=20)
ax.text(8+margin,0+margin,r'x',fontsize=20)

#设置区间
plt.xticks(np.arange(-10,10))
plt.yticks(np.arange(-10,10))

ax.axis('equal')
plt.show()

效果如下：

二. 反馈神经网络

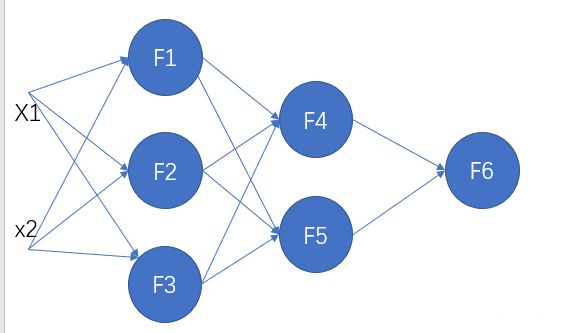
1. 反馈神经网络原理与具体过程

在利用链式求导与梯度下降不断求导时，显然如果拉长求导过程，增加单元，求导过程会产生很多反复的计算，这样就导致了大量冗余的计算。
而反馈神经网络将训练误差看作以权重向量中每个元素为变量的高维函数，通过不断更新权重，寻找误差的最低点。按误差梯度下降的方式，更新权值。

如上图所示，输入x1与x2之后，会得到最终的结果，从f6处输出，为y。
F6(x)=y,那么我们用y与真实值做对比，求误差得到δ

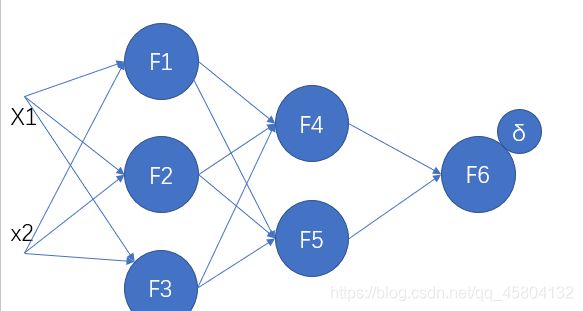
我们将δ反向传播至f4与f5

接下来我们根据误差以及上面提到的公式对权值进行更新。

之后便是不断迭代更新权重，求误差，直到到达迭代上限或者误差很小的情况下，便停止跌代保存参数。

2. 反馈神经网络的激活函数

sigmoid函数

如图它可以将数据规划到[0,1]中，超过阈值便激活，否则便为0.

sigmoid函数：

sigmoid函数的导数：

过深的数学公式什么的这里就不必讲了因为它们并不是必要去钻研的，而且我这里手敲公式出来太麻烦了，所以我们直接来看代码。

3. 代码：

目标是构建一个含有一个输入层，一个隐藏层，一个输出层的反馈神经网络。

代码：

'''
基于python的简单反馈神经网络实现 2021/3/10 by ksks14
'''


import numpy as np
import math 
import random



#生成5和6之间的随机数
def rand(a,b):
    return (b-a)*random.random()+a

#生成一个矩阵
def make_matrix(m,n,fill=0.0):
    mat=[]
    for i in range(m):
        mat.append([fill]*n)
    return mat
#sigmoid函数，激活函数
def sigmoid(x):
    return 1.0/(1.0+math.exp(-x))
#sigmoid函数的导函数   对sigmoid函数求导的过程稿纸上。
def sigmoid_derivate(x):
    return x*(1-x)


class Recurrent_Network:
    #函数内容的初始化
    def __init__(self):
        self.input_n=0
        self.hidden_n=0
        self.output_n=0
        self.input_cells=[]
        self.hidden_cells=[]
        self.output_cells=[]
        self.input_weights=[]
        self.output_weights=[]
    #对数据进行初始化    
    def setup(self,ni,nh,no):
        self.input_n=ni+1
        self.hidden_n=nh
        self.output_n=no
        
        self.input_cells=[1.0]*self.input_n
        self.hidden_cells=[1.0]*self.hidden_n
        self.output_cells=[1.0]*self.output_n
        
        self.input_weights=make_matrix(self.input_n,self.hidden_n)
        self.output_weights=make_matrix(self.hidden_n,self.output_n)
        
        for i in range(self.input_n):
            for h in range(self.hidden_n):
                self.input_weights[i][h]=rand(-0.2,0.2)
        for h in range(self.hidden_n):
            for o in range(self.output_n):
                self.output_weights[h][o]=rand(-2.0,2.0)
    
    #对神经网络前向的计算。
    def predict(self,inputs):
        for i in range(self.input_n-1):
            self.input_cells[i]=inputs[i]
            
        for j in range(self.hidden_n):
            total=0.0
            for i in range(self.input_n):
                total+=self.input_cells[i]*self.input_weights[i][j]
            self.hidden_cells[j]=sigmoid(total)
        for k in range(self.output_n):
            total=0.0
            for j in range(self.hidden_n):
                total+=self.hidden_cells[j]*self.output_weights[j][k]
            self.output_cells[k]=sigmoid(total)
            
        return self.output_cells[:]
    
    def back_propagate(self,case,label,learn):
        self.predict(case)
        #计算输出层的误差
        output_deltas=[0.0]*self.output_n
        for k in range(self.output_n):
            error=label[k]-self.output_cells[k]
            output_deltas[k]=sigmoid_derivate(self.output_cells[k])*error
            
        #计算隐藏层的误差
        hidden_deltas=[0.0]*self.hidden_n
        for j in range(self.hidden_n):
            error=0.0
            for k in range(self.output_n):
                error+=output_deltas[k]*self.output_weights[j][k]
            hidden_deltas[j]=sigmoid_derivate(self.hidden_cells[j])*error
        
        
        #更新输出层权重
        for j in range(self.hidden_n):
            for k in range(self.output_n):
                self.output_weights[j][k]+=learn*output_deltas[k]*self.hidden_cells[j]
                
        #更新隐藏层权重
        for i in range(self.input_n):
            for j in range(self.hidden_n):
                self.input_weights[i][j]+=learn*hidden_deltas[j]*self.input_cells[i]
                
        error=0
        
        for o in range(len(label)):
            error+=0.5*(label[o]-self.output_cells[0])**2
            
            return error
        
        
    def train(self,cases,labels,limit=100,learn=0.05):
        for i in range(limit):
            error=0
            for i in range(len(cases)):
                label=labels[i]
                case=cases[i]
                error+=self.back_propagate(case,label,learn)

    def test(self):
        cases=[
            [0,0],
            [0,1],
            [1,0],
            [1,1],
        ]
        labels=[[0],[1],[1],[0]]
        self.setup(2,5,1)
        self.train(cases,labels,100000,0.05)
        for case in cases:
            print(self.predict(case))
                
if __name__=="__main__":
    nn=Recurrent_Network()
    nn.test()