深度神经网络DNN（六）——导数与梯度

导数

导数就是表示某个瞬间的变化量。它可以定义成下面的式子：
$$\frac{df(x)}{dx}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
上式表示的是函数的导数。左边的符号表示f(x)关于x的导数，即f(x)相对于x的变化程度。表示的导数的含义是，x的“微小变化”将导致函数f(x)的值在多大程度上发生变化。其中，表示微小变化的h无限趋近0。
接下来，我们参考上式，来实现求函数的导数的程序。向h中赋入一个微小值，就可以计算出来了。

def numerical_diff(f, x):
	h = 10e-50
	return (f(x+h) - f(x)) / h

这个函数有两个参数，即“函数f”和“传给函数f的参数x”。乍一看这个实现没有问题，但是实际上这段代码有两处需要改进的地方。

1. 在上面的实现中，因为想把尽可能小的值赋给h（可以话，想让h无限接近0），所以h使用了10e-50（有50个连续的0 的“0.00 . . . 1”）这个微小值。但是，这样反而产生了舍入误差（rounding error）。所谓舍入误差，是指因省略小数的精细部分的数值（比如，小数点第8 位以后的数值）而造成最终的计算结果上的误差。比如，在Python中：

>>> np.float32(1e-50)
0.0

2. 虽然上述实现中计算了函数f在x+h和x之间的差分，但是必须注意到，这个计算从一开始就有误差。如下图所示，“真的导数”对应函数在x处的斜率（称为切线），但上述实现中计算的导数对应的是(x + h) 和x之间的斜率。因此，真的导数（真的切线）和上述实现中得到的导数的值在严格意义上并不一致。这个差异的出现是因为h不可能无限接近0。

如上图所示，数值微分含有误差。为了减小这个误差，我们可以计算函数f在(x+h)和(x−h)之间的差分。因为这种计算方法以x为中心，计算它左右两边的差分，所以也称为中心差分（而(x + h) 和x之间的差分称为前向差分）。下面，我们基于上述两个要改进的点来实现数值微分（数值梯度）：

def numerical_diff(f, x):
	h = 1e-4 # 0.0001
	return (f(x+h) - f(x-h)) / (2*h)

如上所示，利用微小的差分求导数的过程称为数值微分（numerical differentiation）。而基于数学式的推导求导数的过程，则用“解析性”（analytic）一词，称为解析性求解或者解析性求导。比如，y = x²的导数，可以通过dy/dx=2x解析性地求解出来。因此，当x = 2时，y的导数为4。解析性求导得到的导数是不含误差的“真的导数”。

数值微分的例子

现在我们试着用上述的数值微分对简单函数进行求导。先来看一个由下式表示的2次函数：
$$y=0.01x^2+0.1x$$
用Python来实现：

def function_1(x):
	return 0.01*x**2 + 0.1*x

接下来，我们来绘制这个函数的图像：

import numpy as np
import matplotlib.pylab as plt
x = np.arange(0.0, 20.0, 0.1) # 以0.1为单位，从0到20的数组x
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x, y)
plt.show()

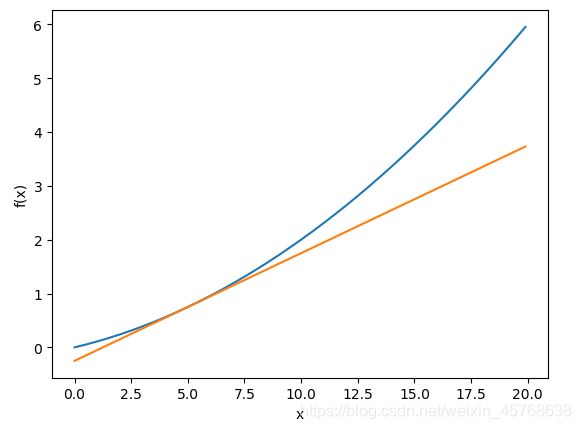
生成的图像：

我们来计算一下这个函数在x = 5和x = 10处的导数：

print(numerical_diff(function_1, 5))
print(numerical_diff(function_1, 10))

# 运行结果
0.1999999999990898
0.2999999999986347

这里计算的导数是f(x)相对于x的变化量，对应函数的斜率。另外，f(x) = 0.01x² + 0.1x 的解析解是df(x)/dx=0.02x+0.1。因此，在x =5 和x = 10处，“真的导数”分别为0.2 和0.3。和上面的结果相比，我们发现虽然严格意义上它们并不一致，但误差非常小。实际上，误差小到基本上可以认为它们是相等的。
现在，我们用上面的数值微分的值作为斜率，画一条直线。结果如图所示，可以确认这些直线确实对应函数的切线：

import numpy as np
import matplotlib.pyplot as plt

def numerical_diff(f, x):
    h = 1e-4 # 0.0001
    return (f(x+h) - f(x-h)) / (2*h)

def function_1(x):
    return 0.01*x**2 + 0.1*x 

def tangent_line(f, x):
    d = numerical_diff(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y
     
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")

tf = tangent_line(function_1, 5)
y2 = tf(x)

plt.plot(x, y)
plt.plot(x, y2)
plt.show()

偏导数

接下来，我们看一下这个函数。
$$f(x_0,x_1)=x_0^2+x_1^2$$
虽然它只是一个计算参数的平方和的简单函数，但是请注意和上例不同的是，这里有两个变量。这个式子可以用Python来实现：

def function_2(x):
	return x[0]**2 + x[1]**2
	# 或者return np.sum(x**2)

这里，我们假定向参数输入了一个NumPy数组。函数的内部实现比较简单，先计算NumPy数组中各个元素的平方，再求它们的和（np.sum(x**2)也可以实现同样的处理）。我们来画一下这个函数的图像：

from pylab import *
from mpl_toolkits.mplot3d import Axes3D

# 生成三维对象
fig=figure()
ax=Axes3D(fig)

# 生成二维网格
X=np.arange(-3,3,0.25)
Y=np.arange(-3,3,0.25)
X,Y=np.meshgrid(X,Y)

# 对每个网格点求函数值
Z=X**2+Y**2

# 作图并展示
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap='hot')
show()

结果如下图所示，是一个三维图像：

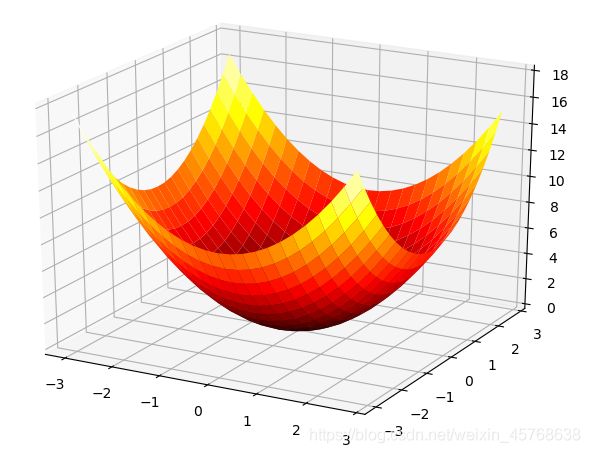
现在我们来求上式的导数。这里需要注意的是，有两个变量，所以有必要区分对哪个变量求导数，即对x₀和x₁两个变量中的哪一个求导数。另外，我们把这里讨论的有多个变量的函数的导数称为偏导数。用数学式表示的话，可以写成：
$$\frac{\partial f}{\partial x_0}、\frac{\partial f}{\partial x_1}$$
怎么求偏导数呢？我们先试着解一下下面两个关于偏导数的问题：
问题1：求x₀=3, x₁=4时，关于x₀的偏导数：

>>> def function_tmp1(x0):
... return x0*x0 + 4.0**2.0
...
>>> numerical_diff(function_tmp1, 3.0)
6.00000000000378

问题2：求x₀=3, x₁=4时，关于x₁的偏导数：

>>> def function_tmp2(x1):
... return 3.0**2.0 + x1*x1
...
>>> numerical_diff(function_tmp2, 4.0)
7.999999999999119

在这些问题中，我们定义了一个只有一个变量的函数，并对这个函数进行了求导。例如，问题1中，我们定义了一个固定x₁=4的新函数，然后对只有变量x₀的函数应用了求数值微分的函数。从上面的计算结果可知，问题1的答案是6.00000000000378，问题2的答案是7.999999999999119，和解析解的导数基本一致。
像这样，偏导数和单变量的导数一样，都是求某个地方的斜率。不过，偏导数需要将多个变量中的某一个变量定为目标变量，并将其他变量固定为某个值。在上例的代码中，为了将目标变量以外的变量固定到某些特定的值上，我们定义了新函数。然后，对新定义的函数应用了之前的求数值微分的函数，得到偏导数。

梯度

在刚才的例子中，我们按变量分别计算了x₀和x₁的偏导数。现在，我们希望一起计算x₀和x₁的偏导数。比如，我们来考虑求x₀=3, x₁=4 时(x₀, x₁)的偏导数：
$$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})$$
像上面这样的由全部变量的偏导数汇总而成的向量称为梯度（gradient）。梯度可以像下面这样来实现：

def numerical_gradient(f, x):
	h = 1e-4 # 0.0001
	grad = np.zeros_like(x) # 生成和x形状相同的数组
	
	for idx in range(x.size):
		tmp_val = x[idx]
		# f(x+h)的计算
		x[idx] = tmp_val + h
		fxh1 = f(x)
		# f(x-h)的计算
		x[idx] = tmp_val - h
		fxh2 = f(x)
		
		grad[idx] = (fxh1 - fxh2) / (2*h)
		x[idx] = tmp_val # 还原值
	
	return grad

函数numerical_gradient(f, x)的实现看上去有些复杂，但它执行的处理和求单变量的数值微分基本没有区别。需要补充说明一下的是，np.zeros_like(x)会生成一个形状和x相同、所有元素都为0 的数组。
函数numerical_gradient(f, x)中，参数f为函数，x为NumPy数组，该函数对NumPy数组x的各个元素求数值微分。现在，我们用这个函数实际计算一下梯度。这里我们求点(3, 4)、(0, 2)、(3, 0) 处的梯度：

>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([ 6., 8.])

>>> numerical_gradient(function_2, np.array([0.0, 2.0]))
array([ 0., 4.])

>>> numerical_gradient(function_2, np.array([3.0, 0.0]))
array([ 6., 0.])

像这样，我们可以计算(x₀, x₁) 在各点处的梯度。上例中，点(3, 4) 处的梯度是(6, 8)、点(0, 2) 处的梯度是(0, 4)、点(3, 0) 处的梯度是(6, 0)。这个梯度意味着什么呢？
为了更好地理解，我们把的梯度画在图上。不过，这里我们画的是元素值为负梯度的向量：

import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)    
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)        
        x[idx] = tmp_val # 还原值        
    return grad

def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)        
        return grad


def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)


def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y
     
if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)
    
    X = X.flatten()
    Y = Y.flatten()
    
    grad = numerical_gradient(function_2, np.array([X, Y]) )
    
    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()

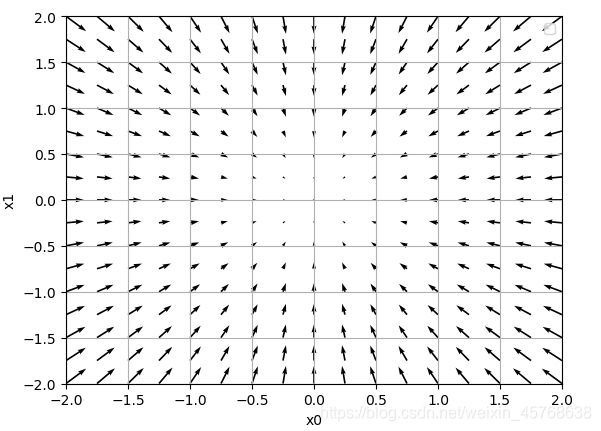
如上图所示，f(x₀,x₁)=x₀²+x₁²的梯度呈现为有向向量（箭头）。观察发现梯度指向函数f(x₀,x₁) 的“最低处”（最小值），就像指南针一样，所有的箭头都指向同一点。其次，我们发现离“最低处”越远，箭头越大。
虽然上图中的梯度指向了最低处，但并非任何时候都这样。实际上，梯度会指向各点处的函数值降低的方向。更严格地讲，梯度指示的方向是各点处的函数值减小最多的方向。这是一个非常重要的性质！

小结

• 导数与数值微分的概念及意义
• 多元函数的偏导数及梯度
• 代码实现导数与梯度求解并可视化