机器学习损失函数小结

概述

  机器学习算法实际上就是模型表征、优化和评估的过程，其中，模型评估决定了后续的优化算法及模型改进的走向，而衡量模型评估的指标就是损失函数。参考李航老师的《统计学习方法》关于损失函数的描述：

监督学习问题是在假设空间$\mathcal{F}$中选取模型$f$作为决策函数，对于给定的输入$X$，由$f(X)$给出相应的输出$Y$，这个输出的预测值$f(X)$与真实值$Y$可能一致也可能不一致，用一个损失函数（loss function）或代价函数（cost function）来度量预测错误的程度。损失函数是$f(X)$和$Y$的非负实值函数，记作$L(Y,f(X))​。

  损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越小，通常模型的性能越好。不同的模型用的损失函数一般也不一样。

  损失函数分为经验风险损失函数和结构风险损失函数，经验风险损失函数指预测结果和实际结果的差别，结构风险损失函数是指经验风险损失函数加上正则项。

  由于模型的输入、输出$(X,Y)$是随机变量，遵循联合分布$P(X,Y)$，所以损失函数的期望为：
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ R_{exp}(f)&=E_…
这是理论上模型$f(X)$关于联合分布$P(X,Y)$的平均意义下的损失，称为风险函数（risk function）或期望损失（expected loss）。学习的目标就是选择期望风险最小的模型，但由于联合分布$P(X,Y)$未知，$R_{exp}(f)$不能直接计算。

  给定一个训练数据集
$$T=\left\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\right\}$$
模型$f(X)$关于训练数据集的平均损失称为经验风险（empirical risk）或经验损失（empirical loss），记作$R_{emp}$：
$$R_{emp}(f)=\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))\text{\hspace{1em}(2)}$$

  期望风险$R_{exp}$是模型关于联合分布的期望损失，经验风险$R_{emp}$是模型关于训练数据集的平均损失。根据大数定律，当样本容量$N$趋于无穷时，经验风险$R_{emp}$趋于期望风险$R_{exp}$。所以，可以利用经验风险估计期望风险。

损失函数、代价函数、目标函数的区别与联系

• 损失函数(loss function)通常是针对单个训练样本而言；
• 代价函数(cost function)通常是针对整个数据集（或一个mini-batch）；
• 目标函数(objective function)表示任意希望被优化的函数。

分类问题中的损失函数

  为了刻画模型输出与样本标签的匹配程度，定义损失函数$L(\bullet ,\bullet$)$:$$Y\times Y$ $\to$ $R$，$L(f(x_i,\theta ),y_i)$越小，表明模型在该样本点匹配得越好。

0-1损失函数

  对于二分类问题，$Y=\{-1，1\}$，我们希望$signf(x_i,\theta )=y_i$，最自然的损失函数为0-1损失，即:
$$L_{0-1}(f,y)=1_{fy\le 0}\text{\hspace{1em}(3)}$$
其中，$1_p$为指示函数（Indicator Function），当且仅当P为真时取值为1，否则取值为0。该损失函数能直观地刻画分类的错误率，但是由于其非凸、非光滑的特点，使得算法很难直接对该函数进行优化。

Hinge损失函数

  0-1损失函数的一个代理损失函数为Hinge损失函数：
$$L_{hinge}(f,y)=max\{0,1-fy\}\text{\hspace{1em}(4)}$$

Hinge损失函数是0-1损失函数相对紧的凸上界，且当$fy\ge 1$时，该函数不对其做任何惩罚。由于Hinge损失在$fy=1$处不可导，因此不能用梯度下降法进行优化，而是用次梯度下降法（Subgra-
dient Descent Method）。

Logistic损失函数

  0-1损失函数的另一个代理损失函数为Logistic损失函数：
$$L_{Logistic}(f,y)=lo{g}_2(1+exp(-fy))\text{\hspace{1em}(5)}$$

Logistic损失函数也是0-1损失函数的凸上界，且该函数处处光滑，因此可以用梯度下降法进行优化。但是，该损失函数对所有的样本点都有所惩罚，因此对异常值相对更敏感一些。

交叉熵损失函数

  当预测值$f\in [-1,1]$时， 另一个常用的代理损失函数为交叉熵（Cross Entroy）损失函数：
$$L_{crossentroy}(f,y)=-lo{g}_2(\frac{1+fy}{2})\text{\hspace{1em}(6)}$$

交叉熵损失函数也是0-1损失函数的光滑凸上界。这四种损失函数的曲线如下图所示：

图1 二分类问题的损失函数

源码如下：

import numpy as np
import math
import matplotlib.pyplot as plt


plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(8, 5))
x = np.linspace(start=-2, stop=3,num =1001,dtype=np.float)
x1=np.linspace(start=-1, stop=1,num =21,dtype=np.float)
logi = np.log(1 + np.exp(-x))/math.log(2)
cross_entropy = -np.log2((1+x1)/2)
boost = np.exp(-x)
y_01 = x < 0
y_hinge = 1.0 - x
y_hinge[y_hinge < 0] = 0
#S_values = [x=3]
plt.plot(x, logi, 'r-', mec='k', label='Logistic Loss', lw=2)
plt.plot(x, y_01, 'g-', mec='k', label='0/1 Loss', lw=2)
plt.plot(x, y_hinge, 'b-',mec='k', label='Hinge Loss', lw=2)
#plt.plot(x, boost, 'm--',mec='k', label='Adaboost Loss',lw=2)
plt.plot(x1, cross_entropy, 'k--',mec='k', label='Cross_entropy Loss',lw=2)
plt.vlines(-1, 0,5,colors = "k", linestyles = "dashed")
plt.vlines(1, 0,5,colors = "k", linestyles = "dashed")

plt.grid(True, ls='--')
plt.legend(loc='upper right')
plt.title('损失函数')
plt.show()

回归问题中的损失函数

  对于回归问题，$Y=R$，我们希望$f(x_i,\theta )\approx y_i$，常用的损失函数包括如下：

平方损失函数

$$L_{squre}(f,y)=(f-y{)}^2\text{\hspace{1em}(5)}$$

平方损失函数时光滑函数，能够用梯度下降法来进行优化。然而，当预测值距离真实值越远时，平方损失函数的惩罚力度越大，因此它对异常类比较敏感。

绝对损失函数

为了解决平方损失函数对异常类比较敏感的问题，可采用绝对损失函数：
$$L_{absoulte}(f,y)=|f-y|\text{\hspace{1em}(6)}$$

绝对损失函数相当于在做中值回归，相比做均值回归的平方损失函数，绝对损失函数对异常点更鲁棒一些。但是，绝对损失函数在$f=y$处无法求导数。

Huber损失函数

  综合考虑可导性和对异常点的鲁棒性，可以采用Huber损失函数：
$$L_{Huber}(f,y)=\{\begin{array}{cc}(f-y{)}^2,& |f-y{|}^2\le \delta \\ 2\delta |f-y|-{\delta }^2,& |f-y|>\delta \end{array}\text{\hspace{1em}(7)}$$

Huber损失函数在$|f-y|$较小时为平方损失，在$|f-y|$较大时为线性损失，处处可导，且对异常点鲁棒。这三种损失函数的曲线如图2所示：

图2 回归问题的损失函数

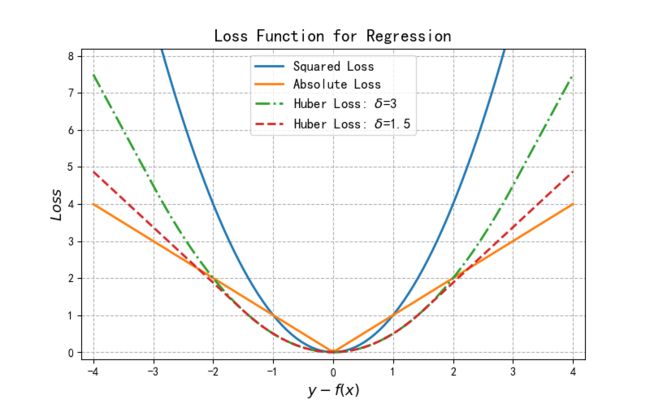
源码如下：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(8, 5))
def huber(res, delta):
    res = abs(res)
    return (res<=delta)*(res**2/2) + (res>delta)*(delta*res-delta**2/2)

plt.axis([-4.2,4.2,-0.2,8.2])
x = np.linspace(-4,4,100)
plt.plot(x, x**2, label="Squared Loss", lw=2)
plt.plot(x,np.where(x>=0,x,-x), label="Absolute Loss", lw=2)
plt.plot(x,huber(x, 3), label="Huber Loss: $\delta$={}".format(3),lw=2, linestyle="-.")
plt.plot(x,huber(x, 1.5), label="Huber Loss: $\delta$={}".format(1.5),lw=2,linestyle="--")
plt.grid(True, ls='--')

plt.legend(loc='upper center', fontsize=12)
plt.xlabel("$y-f(x)$",fontsize=13)
plt.ylabel("$Loss$",fontsize=13)
plt.title("Loss Function for Regression",fontsize=15)