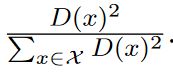K-means算法是最常用的聚类算法之一,本文将对该算法进行解析和numpy复现代码。
K-means解析
定义
K-means基于的一个假设是同类样本点会在特征空间形成簇。在K-means算法中,会给定样本集 X 的 n 个数据点,簇的个数 k。每个簇都有一个类别中心 c。K-means的优化目标如下式,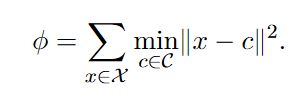
式子的意思是让所有数据点离它们所属的类别中心(最近的中心)的欧式距离之和最小。
求解步骤
求解这个方程一般用下面步骤求解:
- 随机选取 k 个类别中心 C = {c1, c2,···, ck}。
- 把每个数据点归到其最近的类别中心的簇,即给每个点打上假标签。得到 k 个簇集。
- 通过步骤2得到的 k 个簇集,重新计算类别中心,计算方式为,
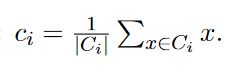
- 重复步骤2和步骤3直到类别中心不再更新为止。
可以看出K-means的求解十分简单,其关键在于类别中心的初始化。最简单的初始化是随机选取 k 个点当作类别中心,但可能会遇到下图情况。下图四个簇对应四个类,当初始点(星)如下图所示时,类别中心无法收敛到正确的位置上。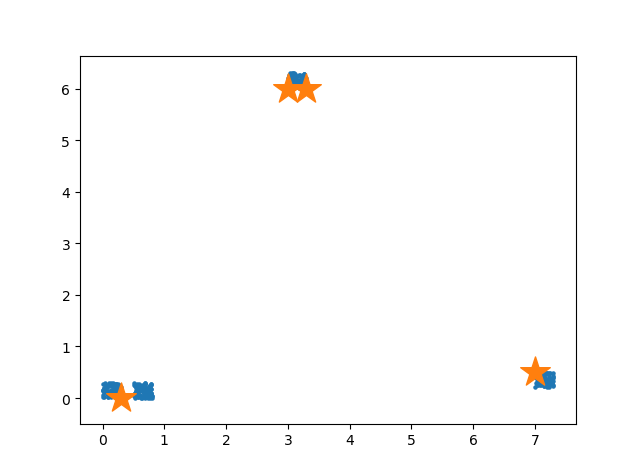
k-means++算法 [1] 就是为解决这个问题所提出的。
K-means++选取初始类别中心步骤为:
关键点在步骤2,其实质是当一个点属于已选取的类别中心的簇的概率越大,它被选取的概率越小。其目的是使得算法尽可能不在同一簇里不选取两个类别中心。不过算法以概率的形式选取,也无法保证不出现上图的情况。因此,一般K-means算法会运行多次,选取目标函数最小的类别中心。
算法代码
初始化形心
使用的是K-means++的方式:
def ini_centers(self,x):
cs = np.array([x[np.random.randint(0, len(x), size = 1).item()]])
for j in range(self.class_num - 1):
for i, c in enumerate(cs):
d = np.sqrt(np.sum((x - c) ** 2, 1).reshape(-1, 1))
if i == 0:
dist = d
else:
dist = np.concatenate((dist, d), 1)
# n, class_num
dist = dist.min(1)
dist = dist**2/sum(dist**2)
index = np.random.choice(np.arange(len(x)), p=dist.ravel())
new_c = x[index]
cs = np.concatenate((cs,[new_c]), 0)
return cs打标签和重新计算类别中心
cnt = 0
flag = True
while flag and cnt < self.max_iter:
# predict
label, score = self.predict(x,cs)
# update
new_cs = np.array([x[label==i].mean(0) for i in range(self.class_num)])
if (cs == new_cs).all(): flag = False
cs = new_cs
cnt+=1预测函数
def predict(self,x,cs):
for i,c in enumerate(cs):
d = np.sqrt(np.sum((x - c)**2,1).reshape(-1,1))
if i == 0:
dist = d
else:
dist = np.concatenate((dist,d),1)
label = dist.argmin(1)
score = dist.min(1).sum()
return label, score多次计算
def fit(self,x):
sc = float("inf")
for t in range(self.n_init):
cs = self.ini_centers(x)
# initial
cnt = 0
flag = True
while flag and cnt < self.max_iter:
# predict
label, score = self.predict(x,cs)
# update
new_cs = np.array([x[label==i].mean(0) for i in range(self.class_num)])
if (cs == new_cs).all(): flag = False
cs = new_cs
cnt+=1
if score < sc:
sc = score
self.cluster_centers_ = cs
return self.cluster_centers_总体函数
class my_Kmeans():
def __init__(self, class_num, max_iter=300, n_init=10):
self.class_num = class_num
self.cluster_centers_ = None
self.max_iter = max_iter
self.n_init = n_init
def ini_centers(self,x):
cs = np.array([x[np.random.randint(0, len(x), size = 1).item()]])
for j in range(self.class_num - 1):
for i, c in enumerate(cs):
d = np.sqrt(np.sum((x - c) ** 2, 1).reshape(-1, 1))
if i == 0:
dist = d
else:
dist = np.concatenate((dist, d), 1)
# n, class_num
dist = dist.min(1)
dist = dist**2/sum(dist**2)
index = np.random.choice(np.arange(len(x)), p=dist.ravel())
new_c = x[index]
cs = np.concatenate((cs,[new_c]), 0)
return cs
def fit(self,x):
sc = float("inf")
for t in range(self.n_init):
cs = self.ini_centers(x)
# initial
cnt = 0
flag = True
while flag and cnt < self.max_iter:
# predict
label, score = self.predict(x,cs)
# update
new_cs = np.array([x[label==i].mean(0) for i in range(self.class_num)])
if (cs == new_cs).all(): flag = False
cs = new_cs
cnt+=1
if score < sc:
sc = score
self.cluster_centers_ = cs
return self.cluster_centers_
def predict(self,x,cs):
for i,c in enumerate(cs):
d = np.sqrt(np.sum((x - c)**2,1).reshape(-1,1))
if i == 0:
dist = d
else:
dist = np.concatenate((dist,d),1)
label = dist.argmin(1)
score = dist.min(1).sum()
return label, score
def fit_predict(self,x):
self.fit(x)
label, score = self.predict(x,self.cluster_centers_)
return label上述代码经试验基本功能完备,但是效果跟效率要差于sklearn库。有可以改进的地方欢迎跟我交流。
[1] Arthur, David and Sergei Vassilvitskii. “k-means++: the advantages of careful seeding.” SODA '07 (2007).