1. 导入数据
library(tidyverse)
library("survival")
library("survminer")
test_data=read.table("survival.txt",header = T,sep = "\t",stringsAsFactors = F)
test_data$over55=ifelse(test_data$age >= 55,1,0)
test_data$over55=as.factor(test_data$over55)
test_data$drug=as.factor(test_data$drug)
head(test_data)
# studytime died drug age over55
# 1 1 1 0 61 1
# 2 1 1 0 65 1
# 3 2 1 0 59 1
# 4 3 1 0 52 0
# 5 4 1 0 56 1
# 6 4 1 0 67 1
summary(test_data)
# studytime died drug age over55
# Min. : 1.00 Min. :0.0000 0:20 Min. :47.00 0:19
# 1st Qu.: 7.75 1st Qu.:0.0000 1:28 1st Qu.:50.75 1:29
# Median :12.50 Median :1.0000 Median :56.00
# Mean :15.50 Mean :0.6458 Mean :55.88
# 3rd Qu.:23.00 3rd Qu.:1.0000 3rd Qu.:60.00
# Max. :39.00 Max. :1.0000 Max. :67.00
attach(test_data)
注意,因为我为了自动补全变量名,使用了attach()。如果没有用这个,像survfit() coxph()这些函数还需要加上data参数
2. KM生存曲线
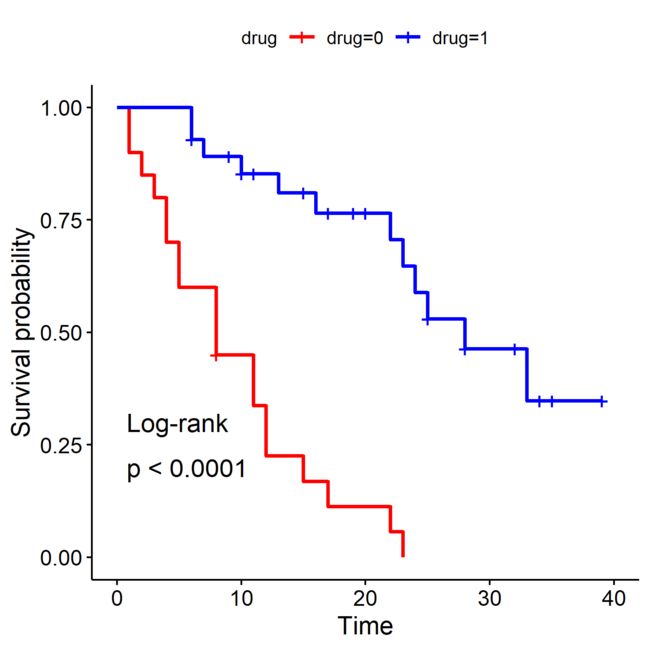
drug_KM=survfit(Surv(studytime,died) ~ drug,data=test_data)
ggsurvplot(drug_KM,data=test_data,legend.title = "drug",pval = TRUE,pval.method=T,palette=c("red","blue"))
ggsave("drug.png",width = 5,height = 5)
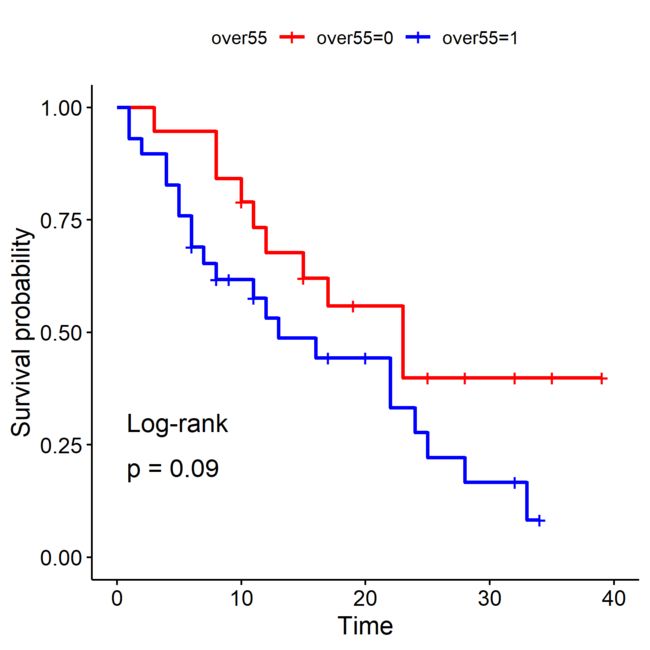
over55_KM=survfit(Surv(studytime,died) ~ over55,data=test_data)
ggsurvplot(over55_KM,data=test_data,legend.title = "over55",pval = TRUE,pval.method=T,palette=c("red","blue"))
ggsave("over55.png",width = 5,height = 5)
3. COX比例风险模型
用两个变量进行Cox-PH model,都是分类变量,当然数值变量也可以做
cox.mod=coxph(Surv(studytime,died) ~ drug + over55)
#描述一下
summary(cox.mod)
# Call:
# coxph(formula = Surv(studytime, died) ~ drug + over55)
#
# n= 48, number of events= 31
#
# coef exp(coef) se(coef) z Pr(>|z|)
# drug1 -2.2632 0.1040 0.4582 -4.940 7.82e-07 ***
# over551 0.9274 2.5278 0.3935 2.356 0.0184 *
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# exp(coef) exp(-coef) lower .95 upper .95
# drug1 0.104 9.6135 0.04238 0.2553
# over551 2.528 0.3956 1.16888 5.4668
#
# Concordance= 0.784 (se = 0.039 )
# Likelihood ratio test= 31.03 on 2 df, p=2e-07
# Wald test = 26.92 on 2 df, p=1e-06
# Score (logrank) test = 34.49 on 2 df, p=3e-08
- exp(coef)就是HR,0.104表示:在控制年龄的情况下,用药的人死亡可能性是没有用药的人的0.104倍
- exp(-coef)为9.6135的解释刚好反过来,表示:在控制年龄的情况下,没有用药的人死亡可能性是用药的人的9.6135倍
- Concordance表示预测一致性
- 后面有三个假设:零假设是b1=b2=b3=...=b_k=0,表征的是模型整体的显著性
4. 森林图
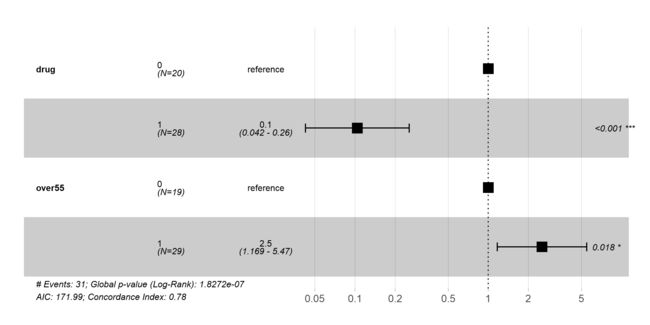
一般文献里面比较关心HR,我们可以用森林图来表示
ggforest(cox.mod, main = '',data = test_data)
ggsave(filename = "cox.mod.png",device = "png",width = 20,height = 10,units = c("cm"))
有时候也能看到KM曲线里面加HR的图,这需要结合KM的结果和COX的结果。
到这里,对于paper的画图已经足够了,如果想深入了解Cox比例风险模型,可以看看下面的内容
5. 采用某个变量前后的模型比较
用LRT (likelihood ratio tests) 比较嵌套模型(一个模型含有另一个模型的全部变量),零假设是两个模型没有差异
cox.mod=coxph(Surv(studytime,died) ~ drug + over55)
cox.mod2=coxph(Surv(studytime,died) ~ over55)
anova(cox.mod2,cox.mod,test = "LRT")
# Analysis of Deviance Table
# Cox model: response is Surv(studytime, died)
# Model 1: ~ over55
# Model 2: ~ drug + over55
# loglik Chisq Df P(>|Chi|)
# 1 -98.062
# 2 -83.994 28.136 1 1.131e-07 ***
p值很小,说明有差异,所以我们不能去掉drug变量
6. cox模型也能用数值型变量
cox.mod3=coxph(Surv(studytime,died) ~ age)
summary(cox.mod3)
exp(coef)等于1.08表示:每增加1岁,风险增加0.08
7. 检查COX PH model的假设
- check linearity
模型中有数值型变量
线性回归里面也有这一步,方法类似 - check the proportional hazard's assumptions
可以简单理解为某个变量对结局事件的影响(回归得到的系数)不随时间而改变
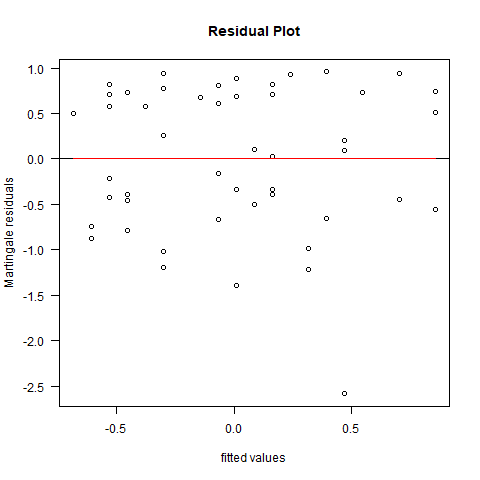
cox.mod4=coxph(Surv(studytime,died) ~ age)
png("Martingale_residuals.png")
plot(predict(cox.mod4),residuals(cox.mod4,type = "martingale"),
xlab = "fitted values",ylab = "Martingale residuals",
main = "Residual Plot",las=1)
#加水平线
abline(h=0)
#画残差的拟合线
lines(smooth.spline(predict(cox.mod4),residuals(cox.mod4,type = "martingale")),col="red")
dev.off()
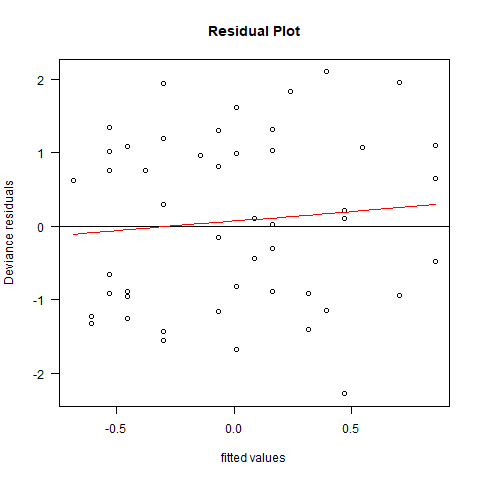
换一种残差检查线性,deviance residuals
png("deviance_residuals.png")
plot(predict(cox.mod4),residuals(cox.mod4,type = "deviance"),
xlab = "fitted values",ylab = "Deviance residuals",
main = "Residual Plot",las=1)
abline(h=0)
lines(smooth.spline(predict(cox.mod4),residuals(cox.mod4,type = "deviance")),col="red")
dev.off()
check proportional hazards assumption
using Schoenfeld test for PH, Ho: HAZARDS are prop, Ha: HAZARDS are NOT prop
结果会返回每个变量,以及整体的p值
cox.zph(cox.mod4)
# chisq df p
# age 0.662 1 0.42
# GLOBAL 0.662 1 0.42
p值较大可以接受原假设。
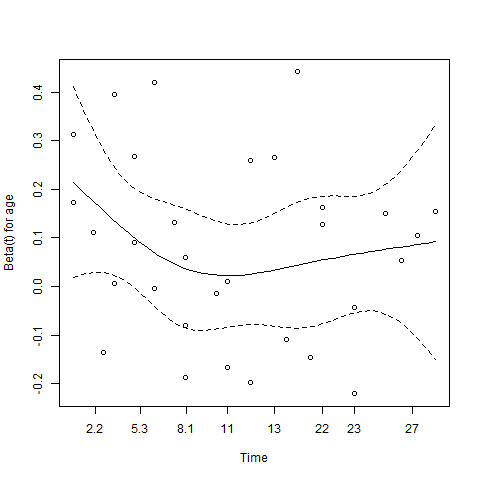
也可以看某个变量的系数(β)是不是随着时间而改变,如果是(也就是说HR随时间而改变),则说明为non-prop hazard
par(mfrow=c(1,1))
png("cox.zph.png")
plot(cox.zph(cox.mod4)[1])
dev.off()
detach(test_data)