1.树
1.1 什么是树?
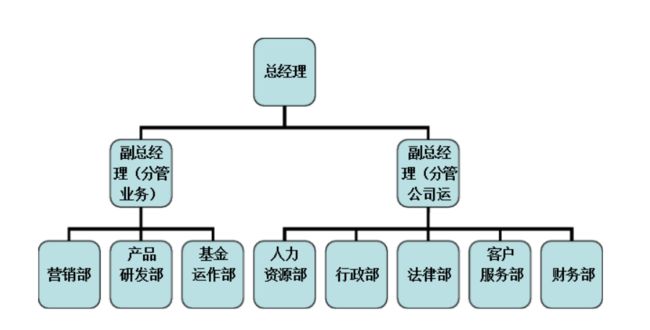
树是一种分层数据的抽象模型,它是一种非常重要的非线性结构.现实生活中最简单的树的例子就是家谱,或者公司的组织架构.如下图所示
1.2树的相关术语
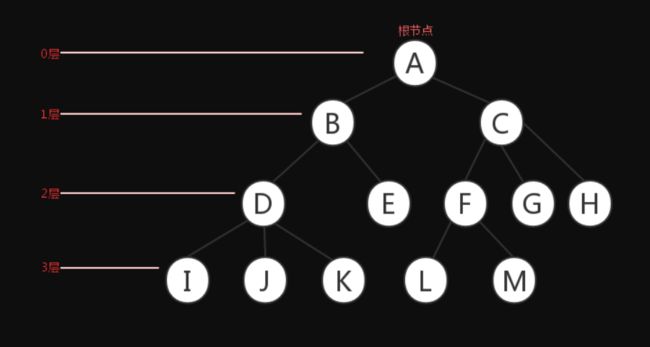
位于树的顶部叫做跟节点,他没有父节点.其他节点都都是子节点,没有子元素的节点称为外部节点或者叶节点.每个节点都有都有层次,比如图中b节点层次为1,A节点层次为0,树中最大的层次称为该树的深度.
有关树的另一个术语就是子树/子树有节点和它的后台节点组成,例如节点BDE就组成了上图中的一个子树.
1.3 二叉树和二叉搜索树
二叉树在计算机中应用非常广泛,它是一中特殊的树,二叉树中的每个节点最多只能拥有两个节点:一个是左侧子节点,另一个是右侧子节点.这个定义可以有助于我们可以更高效得对数中数据进行增删改查等操作.
二叉搜索树(BST):是二叉树中的一种.但是只允许在节点的左侧储存比节点小的值,在右侧节点储存比节点大或等于的值.
下面我们来实现二叉搜索树.
首先我们先创建Node类来表示二叉搜索树中的每个节点.代码如下
class Node{
constructor(key){
this.key = key;//节点的值
this.left= null;// 左侧节点引用
this.right = null;// 右侧节点引用
}
}
和链表一样,我们将通过两个指针(引用)来表示节点之间的关系,在二叉搜索树树中每个节点都有一个左侧节点和右侧节点的指针(引用)用来储存它的子节点.
接下来我们来实现二叉搜索树,下面是一个树需要实现的具体方法
- insert(key): 向树中插入一个键
- search(key):向树中查找一个键,如果节点存在则返回true, 否者返回false.
- min(): 返回树中最小的键.
- max(): 返回树中最大的键.
- remove(key): 从树中移除某个键.
1.3.1实现树的插入
class BinaSearchTree {
constructor() {
this.root = null;
}
// 向二叉树中插入正确节点的方法.
static insertNode(node, root) {
// 如果当前插入节点的key比根节点的key值小, 则将节点插入到根节点的左侧
// 而且当前根节点左侧不存在节点,则插入否者递归插入
if (node.key < root.key) {
if (root.left) {
this.insertNode(node, root.left)
} else {
console.log(root)
root.left = node
}
} else {
if (root.right) {
this.insertNode(node, root.right)
} else {
root.right = node;
}
}
}
// 向二叉树插入的数据
insert(key) {
let node = new Node(key);
// 如果根节点不为空,调用insertNode方法插入正确的节点
if (this.root !== null) {
BinaSearchTree.insertNode(node, this.root)
} else {
// 向根节点插入数据
this.root = node;
}
}
}
bst.insert(9);
bst.insert(5);
bst.insert(4);
bst.insert(12);
bst.insert(20);
console.log(bst);
BinaSearchTree类的insert方法用于向二叉搜索树中插入一个新节点,.如果树的根节点为空,则直接向树的根节点插入的新节点,否者调用insertNode方法来传入树的根节点和要插入的新节点.
insertNode方法会帮助我们找到新节点应该插入的正确位置,它接受两个参数,第一个参数为当前插入的新节点, 第二个参数为要插入的根节点, 如果当前插入的新节点的键比当前根节点的key小,那么此时检索当前根节点的左侧子节点, 如果它没有左侧子节点,则在跟节点的左侧插入新节点, 否者需要通过递归调用insertNode.继续找到树的下一层,此时应该比较的就是当前根节点的左侧子节点树.
同理可得,如果插入的的新节点的键比当前根节点的键大,同时根节点的右侧没有子节点,那么就在那个位置插入新节点,否者则递归调用insertNode方法,此时我们一个比较的是当前根节点的右侧节点树.
1.3.2树的遍历
遍历一个树是指访问树的每一个节点并对其进行某种操作的过程.一般的,访问树的所有节点总共有三种方法:中序、先序、后序.
中序遍历
中序遍历是一种以上行访问顺序访问BST中所有节点的遍历方式,也就是从小到大的顺序访问所有节点.中序遍历针对每棵树都是左根右的顺序数据,下面我们看看它的实现.
inOrderTraverse(callback){
this.inOrderTraverseNode(this.root,callback)
}
inOrderTraverse方法接受一个回调函数作为参数.回调函数定义我们对遍历的每个节点对应的操作.用于在BST中最常的实现的算法就是递归.这里使用了一个辅助方法,来接受一个对应的节点和回调函数作为参数,辅助方法的实现如下.
inOrderTraverseNode(node,callback){
if(node === null) return;
this.inOrderTraverseNode(node.left,callback)
callback(node.key);
this.inOrderTraverseNode(node.right,callback)
}
要中序遍历一个树,首先我们要检查以参数形式传入的节点是否为null, 这就是要停止递归继续执行的判断条件,然后我们递归调用相同的函数来访问左侧节点,接着对根节点进行一些操作即调用对应的callback并传入对应的节点值,然后在访问右侧子节点.
接着我们试着在之前的树调用inOrderTraverse方法
bst.inOrderTraverse(key =>{
console.log(key)
})
我们想inOrderTraverse方法传入一个回调函数, 这个回调函数的作用就是在控制台打印当前节点值此时,我们可以看到控制台依次打印出4,5,9,12,20.
先序遍历
先序遍历是以优先以后代节点的顺序访问的每个节点.先序遍历针对每棵树都是根左右的顺序遍历.
preOrderTraverse(callback){
this.preOrderTraverseNode(this.root,callback)
}
preOrderTraverseNode(node,callback){
if( node === null )return;
callback(node.key)
this.preOrderTraverseNode(node.left,callback);
this.preOrderTraverseNode(node.right,callback);
}
先序遍历的实现和中序遍历类似,与其不同的是,先序遍历会先遍历节点本身,遍历节点的的左侧子节点,最后是节点的右侧子节点.
后序遍历
后序遍历则是先访问节点的后代节点,在访问节点的本身,即按照左右根的顺序进行遍历.
portOrderTraverse(callback){
this.portOrderTraverseNode(this.root,callback)
}
portOrderTraverseNode(node,callback){
if(node === null) return;
this.portOrderTraverseNode(node.left,callback);
this.portOrderTraverseNode(node.right,callback);
callback(node.key)
}
中序遍历和先序遍历和后序遍历的实现都非常相似,唯一不同的是,相应的执行顺序.
1.3.3树的查找和删除.
在树中我们经常有三种执行的搜索类型
- 搜索最小值
- 搜索最大值
- 搜索特定值
搜索最大值和最小值
在二叉搜索树中,你会发现最小的值在的最后一层的最左侧节点,这就是这棵树中最小的键,同理在树的最后一层的最右侧节点就是这棵树总共最大的键.
- 搜索树的最大值
max(){
return this.maxNode(this.root);
}
maxNode(node){
let current = node;
// 遍历当前接地的左侧节点
while(current !== null && current.left !== null){
current = current.left
};
return current
}
- 搜索树的最小值
min(){
return this.minNode(this.root);
}
minNode(node){
let current = node;
// 遍历当前节点的右侧节点
while(current !== null && current.right !== null){
current = current.right
};
return current
}
上面的 minNode方法内部我们会遍历树的左边, 直到当前节点的为空且节点的左侧也为空时则停止并返回当前节点.maxNode方法也是相同的逻辑,只不过maxNode遍历的是树的右边.
搜索一个树的特定值
search(key){
return BinaSearchTree.searchNode(this.root,key)
}
searchNode(node,key){
// 如果节点为空则返回false 表示没有找打对应的节点
if(node === null) return false;
// 如果key小于当前节点key,则递归遍历当前节点的左侧节点,
if(key < node.key){
return this.searchNode(node.left,key)
}else if(key > node.key){
return this.searchNode(node.right, key)
}else{
// 当节点的key和要要查找的key相同时直接返回true 表示查找到了
return true;
}
}
上面的search方法用来搜索是否存在节点为key的节点, 如果有则返回true,否者返回false,这个方法同样的需要一个searchNode辅助方法来方便我们在树中寻找任意一棵树的一个特定节点值. searchNode方法会接受两个参数,第一个参数为当前搜索的节点, 第二个参数为有查找的键值, searchNode方法内部首先会判断节点是否为空, 如果为空,直接返回false, 如果当前节点的key小于要查找的key,则我们需要继续查找节点的左侧节点来进行对比,因此我们会用递归来深层查找节点的key,同理当节点的key小于当前要查找的key,我们则需要继续查找当前节点的右侧节点来进行对比,否者此时说明此时节点的key等于当前对应的key,此时表明找到了,我们直接返回true.
移除一个节点
移除一个节点的算法实现时最复杂的,因为它要考虑的场景非常多,当然它同样的需要递归来来实现.
remove(key){
this.root = this.removeNode(this.root,key);
}
remove方法接受要删除的键,并且调用了removeNode方法,传入了root和要移除的键.
removeNode(node, key) {
// 如果节点为空, 则返回 null
if (node === null) return null;
// 如果key小于节点的key, 则递归当前当前的节点的左侧节点
// 并更新节点的左侧节点, 并将新节点返回
if (key < node.key) {
// 更新节点的左侧节点, 并赋值为当前递归删除节点的新节点
node.left = this.removeNode(node.left, key);
return node
} else if (key > node.key) {
node.right = this.removeNode(node.right, key);
return node
} else {
// 移除一个叶节点
if (node.left === null && node.right === null) {
node = null;
return node;
}
// 移除有一个左侧或者右侧子节点的节点
if (node.left === null) {
node = node.right;
return node
} else if (node.right === null) {
node = node.left;
return node
}
//移除有两个子节点的节点
const minNode = this.minNode(node.right);
node.key = minNode.key;
node.right = this.removeNode(node.right, minNode.key);
return node
}
}
在树中移除一个节点第一种情况是该节点是一个没有左侧或右侧子节点的叶节点,此时我们给这个的节点赋值为null来移除它,并将其返回,此时父节点的指针会接受到这个值.此时我们能实现在父节点的指针上left或者right上删除该节点.
现在我们来处理第二种情况,移除一个带有左侧子节点或者右侧子节点, 通过这个子节点没有左侧节点只有右侧节点,此时我们只需要将当前节点的引用改为对它右侧子节点的引用,并返回更新后的节点.如果这个节点没有右侧子节点,同理我们我只需要将对它的引用对它左侧节点的引用.并返回更新后的节点,
现在我们来处理第三种情况,也是最复杂的情况,那就是移除一个有两个子节点的节点,即左侧子节点和右侧子节点.有移除一个有两个子节点的节点,需要有如下四个步骤:
- 当找到要删除的节点时,需要找到它的右子树的最小的节点
- 如果用它的右侧子树的最小节点的键去更新这个节点值.
- 将右侧子树中的最小节点删除
- 最后向他的父节点返回更新后的节点的引用.