高等数学——积分

1. 不定积分

1.1 定义

在区间上，函数的带有任意常数项的原函数称为（或）在区间上的不定积分，记作其中记号称为积分号，称为被积函数，称为被积表达式，称为积分变量。

由定义可知：

如果是在区间上的一个原函数，那么就是的不定积分，即因而不定积分可以表示的任意一个原函数。
由于是的原函数，所以或
又由于是的原函数，所以或记作
由此可见，微分运算（以记号表示）与求不定积分的运算（简称积分运算，以记号表示）是互逆的，当记号与连在一起时，或者相互抵消，或者抵消后差一个常数。

定理连续函数一定有原函数。

image.png

1.2 基本积分表

1.3 不定积分的性质

性质 1 设函数及的原函数存在，则

性质 2 设函数的原函数存在，为非零常数，则

1.4 积分法

第一类换元积分法 设具有原函数，可导，则有换元公式

第二类换元积分法 设是单调的、可导的函数，并且，又设具有原函数，则有换元公式其中是的反函数。

分部积分法 设函数及具有连续导数，那么，两个函数乘积的导数公式为移项得对这个等式两边求不定积分，得此即为分部积分公式，简便写法为

2. 定积分

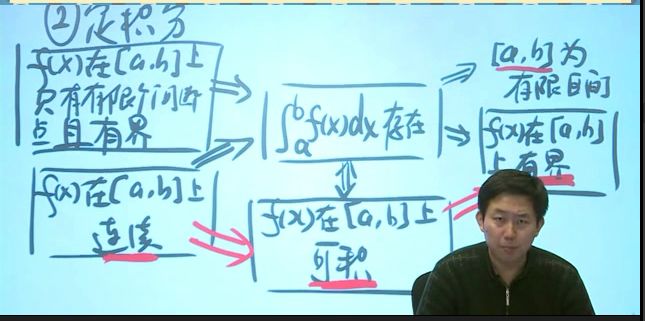
2.1 两个充分条件

定理 1 设在上连续，则在上可积。

定理 2 设在上有界，且只有有限个间断点，则在上可积。

2.2 定积分的性质

规定

当时，
当时，

性质 1

性质 2

性质 3 设，则

性质 4 如果在区间上，则

性质 5 如果在区间上，则

推论 1 如果在区间上，则

推论 2

性质 6 设及分别是在区间上的最大值及最小值，则

性质 7 (积分中值定理) 如果在区间上连续，则在上至少存在一个点，使下式成立：

2.3 微积分基本公式

定理 1 如果在区间上连续，则积分上限的函数在上可导，并且它的导数

定理 2 如果在区间上连续，则函数就是在上的一个原函数。

定理 3 如果是连续函数在上的一个原函数，则

定积分的换元法 假设在区间上连续，函数满足条件：
（1）;
（2）在上具有连续导数，且其值域，则有

定积分的分部积分法 即已经积出的部分可以先用上下限代入。

3. 反常积分

3.1 无穷限的反常积分

定义 1 设在区间上连续，取，如果极限存在，则称此极限为函数在无穷区间上的反常积分，记作，即
这时也称反常积分收敛，如果上述极限不存在，则函数在无穷区间上的反常积分就没有意义，习惯上称为反常积分发散。

类似的，设在区间上连续，取，如果极限存在，则称此极限为函数在无穷区间上的反常积分，记作，即
这时也称反常积分收敛，如果上述极限不存在，则称反常积分发散。

设在区间上连续，如果反常积分和都收敛，则称上述两反常积分之和为函数在无穷区间上的反常积分，记作，即
这时也称反常积分收敛，否则，称反常积分发散。

3.2 无界函数的反常积分

如果函数在的任一领域内都无界，那么点称为函数的瑕点（也称为无界间断点），无界函数的反常积分又称为瑕积分。

定义 2 设函数在区间上连续，点为的瑕点，取，如果极限存在，则称此极限为函数在上的反常积分，记作，即这时也称反常积分收敛，如果上述极限不存在，则称反常积分发散。

类似的，设函数在区间上连续，点为的瑕点，取，如果极限存在，则定义否则，就称反常积分发散。

设函数在区间上除点外连续，点为的瑕点，如果两个反常积分和都收敛，则定义否则，就称反常积分发散。

4. 微分方程

3.1 定义

一般的，凡是表示未知函数、未知函数的导数与自变量之间关系的方程，叫做微分方程，有时也简称方程。微分方程中所出现的未知函数的最高阶导数的阶数，叫做微分方程的阶。

一般的，阶微分方程的形式是

3.2 微分方程的解法

3.2.1 可分离变量的微分方程

一般的，如果一个一阶微分方程能写成的形式，即能把微分方程写成一段只包含的函数和，另一端只含的函数和，那么原方程就称为可分离变量的微分方程。

对式两端积分设即依次为和的原函数，于是有式即为方程的隐式解，也称为微分方程的隐式通解。

3.2.2 齐次方程

如果一阶微分方程可化为的形式，那么就称这方程为齐次方程。

在齐次方程中，引入未知函数（其中），就可将它化为可分离变量的方程。

3.2.3 线性方程

定义 1 方程叫做一阶线性微分方程。如果则方程称为齐次的，否则称为非齐次的。

此类方程的解为：其对应的齐次方程的通解与非齐次方程的一个特解之和。
由
分离变量后求解得到：
再用常数变易法来求解非齐次方程的特解：将的通解中的常数替换为的未知函数，即做变换
于是
将和代入进行求解，得到

即为方程的特解。
所以方程的解为：

定义 2 一阶线性方程，形如

解法：两边同乘积分因子得

两边积分得

于是

3.3 函数的线性相关性

对于两个函数构成的函数组，如果两函数的比为常数，则它们是线性相关的，否则就线性无关。