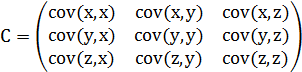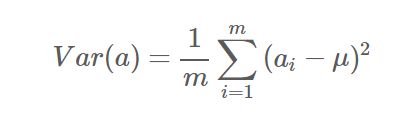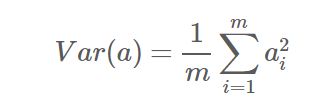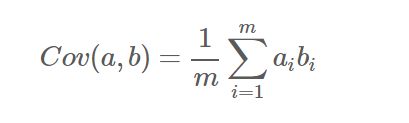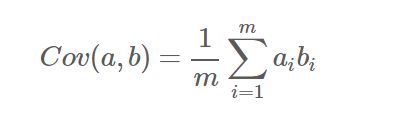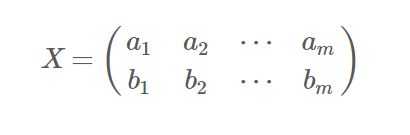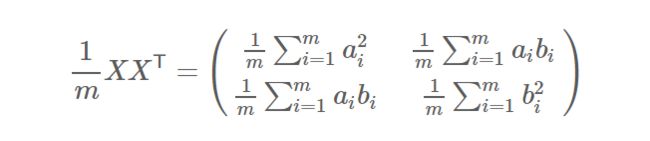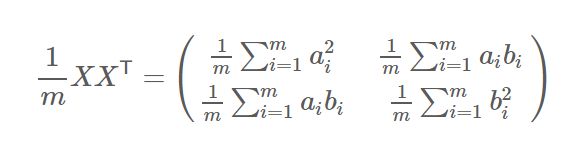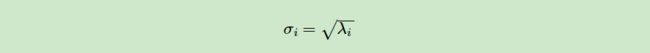本文内容是机器学习算法原理介绍系列的最后一篇,承接之前文章的思路,主要是介绍PCA算法的详细原理及sklearn的官方demo
一、为什么要使用PCA
先来看一下下面几个例子
1、 比如拿到一个汽车的样本,里面既有以“千米/每小时”度量的最大速度特征,也有“英里/小时”的最大速度特征,显然这两个特征有一个多余。------特征的含义相同
2、 拿到一个数学系的本科生期末考试成绩单,里面有三列,一列是对数学的兴趣程度,一列是复习时间,还有一列是考试成绩。我们知道要学好数学,需要有浓厚的兴趣,所以第二项与第一项强相关,第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢?|"learn"与"study"----强关联项|语义相同
3、 拿到一个样本,特征非常多,而样例特别少,这样用回归去直接拟合非常困难,容易过度拟合。比如北京的房价:假设房子的特征是(大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数),搞了这么多特征,结果只有不到十个房子的样例。要拟合房子特征->房价的这么多特征,就会造成过度拟合。-----------特征的数量偏多
二、预备知识---协方差的介绍
协方差:简单来讲是用于评测或者衡量两个随机变量(维度)之间的关联程度,协方差的绝对值越大,则表明两者之间的协同关联度越高,为0的时候则表示两个维度之间相互独立
从协方差的定义上我们也可以看出一些显而易见的性质,如:
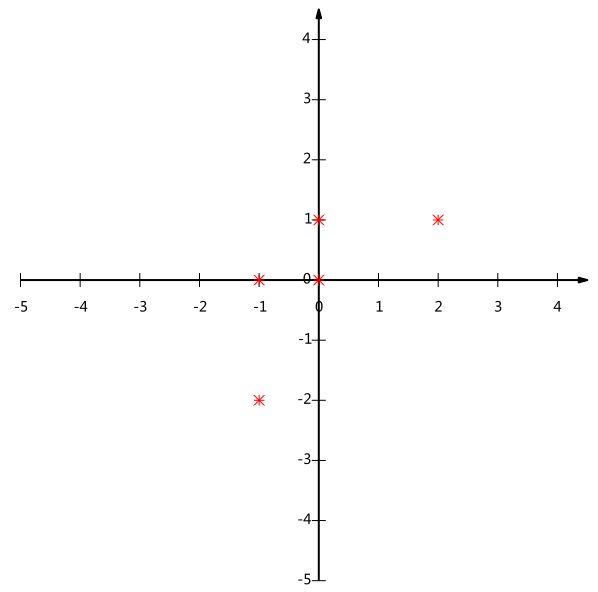
举一个简单的三维例子
由上述可以看出,协方差矩阵是一个对称矩阵,且对角线存放每一维度的方差
三、PCA 原理剖析(原文链接:http://blog.codinglabs.org/articles/pca-tutorial.html)
下面先来看一个高中就学过的向量运算:
内积
两个维数相同的向量的内积被定义为:
(a1,a2,⋯,an)T⋅(b1,b2,⋯,bn)T=a1b1+a2b2+⋯+anbn
内积运算将两个向量映射为一个实数。其计算方式非常容易理解,但是其意义并不明显。下面我们分析内积的几何意义。假设A和B是两个n维向量,我们知道n维向量可以等价表示为n维空间中的一条从原点发射的有向线段,为了简单起见我们假设A和B均为二维向量,则A=(x1,y1),B=(x2,y2)。则在二维平面上A和B可以用两条发自原点的有向线段表示,见下图:
好,现在我们从A点向B所在直线引一条垂线。我们知道垂线与B的交点叫做A在B上的投影,再设A与B的夹角是a,则投影的矢量长度为|A|cos(a),其中|A|=x21+y21−−−−−−√是向量A的模,也就是A线段的标量长度。
注意这里我们专门区分了矢量长度和标量长度,标量长度总是大于等于0,值就是线段的长度;而矢量长度可能为负,其绝对值是线段长度,而符号取决于其方向与标准方向相同或相反。
到这里还是看不出内积和这东西有什么关系,不过如果我们将内积表示为另一种我们熟悉的形式:
A⋅B=|A||B|cos(a)
现在事情似乎是有点眉目了:A与B的内积等于A到B的投影长度乘以B的模。再进一步,如果我们假设B的模为1,即让|B|=1,那么就变成了:
A⋅B=|A|cos(a)
也就是说,设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度!这就是内积的一种几何解释,也是我们得到的第一个重要结论。在后面的推导中,将反复使用这个结论。
基
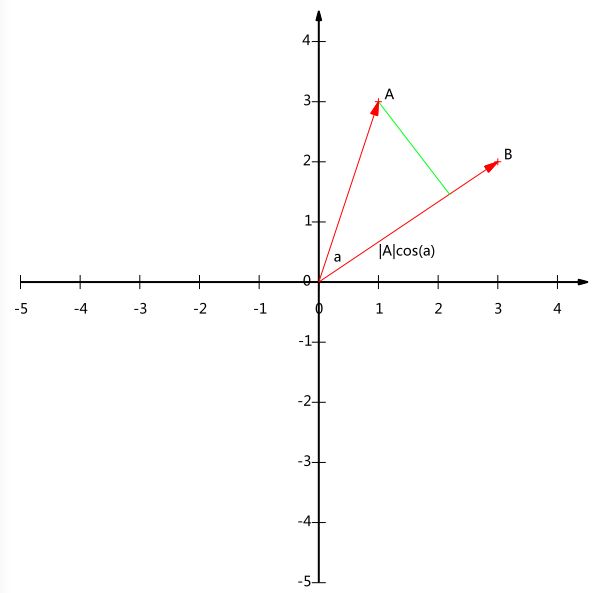
下面我们继续在二维空间内讨论向量。上文说过,一个二维向量可以对应二维笛卡尔直角坐标系中从原点出发的一个有向线段。例如下面这个向量:
在代数表示方面,我们经常用线段终点的点坐标表示向量,例如上面的向量可以表示为(3,2),这是我们再熟悉不过的向量表示。
不过我们常常忽略,只有一个(3,2)本身是不能够精确表示一个向量的。我们仔细看一下,这里的3实际表示的是向量在x轴上的投影值是3,在y轴上的投影值是2。也就是说我们其实隐式引入了一个定义:以x轴和y轴上正方向长度为1的向量为标准。那么一个向量(3,2)实际是说在x轴投影为3而y轴的投影为2。注意投影是一个矢量,所以可以为负。
更正式的说,向量(x,y)实际上表示线性组合:
x(1,0)T+y(0,1)T
不难证明所有二维向量都可以表示为这样的线性组合。此处(1,0)和(0,1)叫做二维空间中的一组基。
再例如,(1,1)和(-1,1)也可以成为一组基。一般来说,我们希望基的模是1,因为从内积的意义可以看到,如果基的模是1,那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了!实际上,对应任何一个向量我们总可以找到其同方向上模为1的向量,只要让两个分量分别除以模就好了。
现在,我们想获得(3,2)在新基上的坐标,即在两个方向上的投影矢量值,那么根据内积的几何意义,我们只要分别计算(3,2)和两个基的内积
基变换的矩阵展示
下面我们找一种简便的方式来表示基变换。还是拿上面的例子,想一下,将(3,2)变换为新基上的坐标,就是用(3,2)与第一个基做内积运算,作为第一个新的坐标分量,然后用(3,2)与第二个基做内积运算,作为第二个新坐标的分量。实际上,我们可以用矩阵相乘的形式简洁的表示这个变换
为了避免过于抽象的讨论,我们仍以一个具体的例子展开。假设我们的数据由五条记录组成,将它们表示成矩阵形式:
其中每一列为一条数据记录,而一行为一个字段。为了后续处理方便,我们首先将每个字段内所有值都减去字段均值,其结果是将每个字段都变为均值为0(这样做的道理和好处后面会看到)。
我们看上面的数据,第一个字段均值为2,第二个字段均值为3,所以变换后:
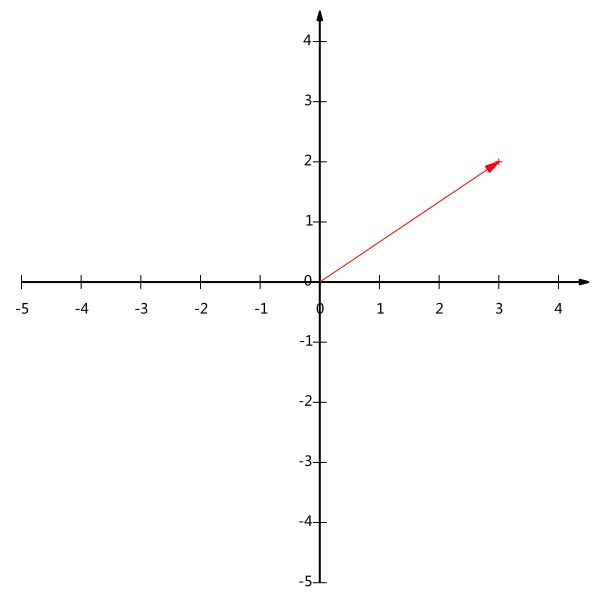
我们可以看下五条数据在平面直角坐标系内的样子:
现在问题来了:如果我们必须使用一维来表示这些数据,又希望尽量保留原始的信息,你要如何选择?
通过上一节对基变换的讨论我们知道,这个问题实际上是要在二维平面中选择一个方向,将所有数据都投影到这个方向所在直线上,用投影值表示原始记录。这是一个实际的二维降到一维的问题。
那么如何选择这个方向(或者说基)才能尽量保留最多的原始信息呢?一种直观的看法是:希望投影后的投影值尽可能分散。
以上图为例,可以看出如果向x轴投影,那么最左边的两个点会重叠在一起,中间的两个点也会重叠在一起,于是本身四个各不相同的二维点投影后只剩下两个不同的值了,这是一种严重的信息丢失,同理,如果向y轴投影最上面的两个点和分布在x轴上的两个点也会重叠。所以看来x和y轴都不是最好的投影选择。我们直观目测,如果向通过第一象限和第三象限的斜线投影,则五个点在投影后还是可以区分的。
下面,我们用数学方法表述这个问题。
方差---表征离散程度,投影尽可能分散,也就是方差值变大
由于上面我们已经将每个字段的均值都化为0了,因此方差可以直接用每个元素的平方和除以元素个数表示:
协方差----目标是使得各特征之间相互独立,没有线性关系,从而避免特征之间的信息重复
至此,我们得到了降维问题的优化目标: 将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的K个方差)。
假设我们只有a和b两个字段,那么我们将它们按行组成矩阵X:
然后我们用X乘以X的转置,并乘上系数1/m:
设我们有m个n维数据记录,将其按列排成n乘m的矩阵X,设C=1/m*XXT,则C是一个对称矩阵,其对角线分别个各个字段的方差,而第i行j列和j行i列元素相同,表示i和j两个字段的协方差。
PCA算法总结
设有m条n维数据。
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵C=1/m*XXT
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
四、PCA步骤中特征值和特征向量的求解
1.常用的数学方法---针对方形矩阵
2.SVD奇异求解----任何形式的矩阵
1.特征值和特征向量
我们首先回顾下特征值和特征向量的定义如下:
[图片上传中...(image.png-5ae866-1550134434773-0)]
2.SVD奇异值求解
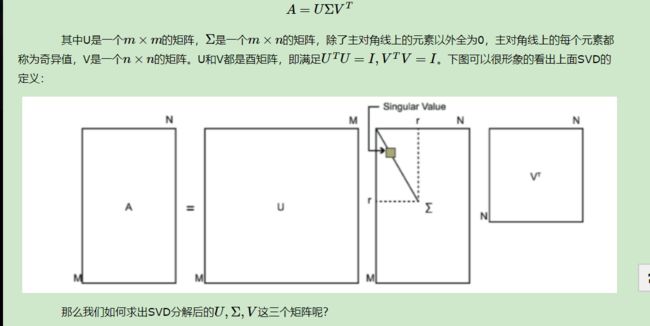
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵,那么我们定义矩阵A的SVD为:
如果我们将A的转置和A做矩阵乘法,那么会得到n×n的一个方阵ATA。既然ATA是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
(ATA)vi=λivi
这样我们就可以得到矩阵ATA的n个特征值和对应的n个特征向量v了。 将ATA的所有特征向量张成一个n×n的矩阵V,就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。
如果我们将A和A的转置做矩阵乘法,那么会得到m×m的一个方阵AAT。既然AAT是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
(AAT)ui=λiui
这样我们就可以得到矩阵AAT的m个特征值和对应的m个特征向量u了。 将AAT的所有特征向量张成一个m×m的矩阵U,就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量
注:针对上述为什么ATA就是V,AAT就是U,进行如下证明
U和V我们都求出来了,现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0,那我们只需要求出每个奇异值σ就可以了。
最后值得一提的是奇异值σ和特征值λ之间的关系
五、sklearn 实例demo
1.load_iris()
鸢尾类别是3个,class为3
每一类50个数据,总共数据量为150
每一个数据的特征维度为4
数据是以json的形式存储,键分别为data,target
parameters:
return_X_y:boolean,default=False
如果为真 返回(data,target)
data=load_iris()
print (data.target[[10,25]])表示返回的是第10,25两个样本所属的类别编号
IncrementalPCA
主要是为了解决单机内存限制的。有时候样本数量过大,直接去拟合数据会让内存爆炸的,此时可用IncrementalPCA来解决这个问题。
parameters
1.n_components: 整数,PCA降维后的维度,大于1且小于数据数量
2.whiten:判断是否进行白化。所谓白化,就是对降维后的数据的每个特征进行归一化,让方差都为1.对于PCA降维本身来说,
一般不需要白化。如果你PCA降维后有后续的数据处理动作,可以考虑白化。默认值是False,即不进行白化。
3.copy default=True 一般不懂
4.batch_size init 数据要分的批数
attributes:
1.components with maximum variance 即参与进行降维的主成分 array
2.explained_variance_ : array Variance explained by each of the selected components. 主成分返回的方差数组
3.explained_variance_ratio_ :Percentage of variance explained by each of the selected components.
If all components are stored, the sum of explained variances is equal to 1.0.
4.singular_values_,奇异值
5.mean_,待降维矩阵的均值
6.var_,待降维矩阵的方差
methods:
1.fit(x) 见之前文章 不详述 Returns the instance itself.
2.fit_transform(x) 见之前文章 不详述 Transformed array.
3.get_params_()
4.partial_fit(x)Returns the instance itself.
PCA
parameters:除了上述的参数外
1.svd_solver:即指定奇异值分解SVD的方法,由于特征分解是奇异值分解SVD的一个特例,一般的PCA库都是基于SVD实现的。
有4个可以选择的值:{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大,
数据维度多同时主成分数目比例又较低的PCA降维,它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD,
使用了scipy库对应的实现。arpack和randomized的适用场景类似,区别是randomized使用的是scikit-learn自己的SVD实现,
而arpack直接使用了scipy库的sparse SVD实现。默认是auto,即PCA类会自己去在前面讲到的三种算法里面去权衡,
选择一个合适的SVD算法来降维。一般来说,使用默认值就够了。
2.tol : float >= 0, optional (default .0)
Tolerance for singular values computed by svd_solver == ‘arpack’.
3.random_state : int
f int, random_state is the seed used by the random number generator; If RandomState instance,
random_state is the random number generator; If None,
the random number generator is the RandomState instance used by np.random. Used when svd_solver == ‘arpack’ or ‘randomized’.
attributes:见上述的IncrementalPCA
常用methods
1.fit(x)
2.fit_transform(x)
3.get_params(x)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris#鸢尾
from sklearn.decomposition import PCA
from sklearn.decomposition import IncrementalPCA
iris=load_iris()#导入数据集合
x=iris.data
y=iris.target
n_components=2
ipca=IncrementalPCA(n_components=n_components,batch_size=10)
x_ipca=ipca.fit_transform(x)#返回的是降维后的150个数据
pca=PCA(n_components=n_components)
x_pca=pca.fit_transform(x)
colors = ['navy', 'turquoise', 'darkorange']
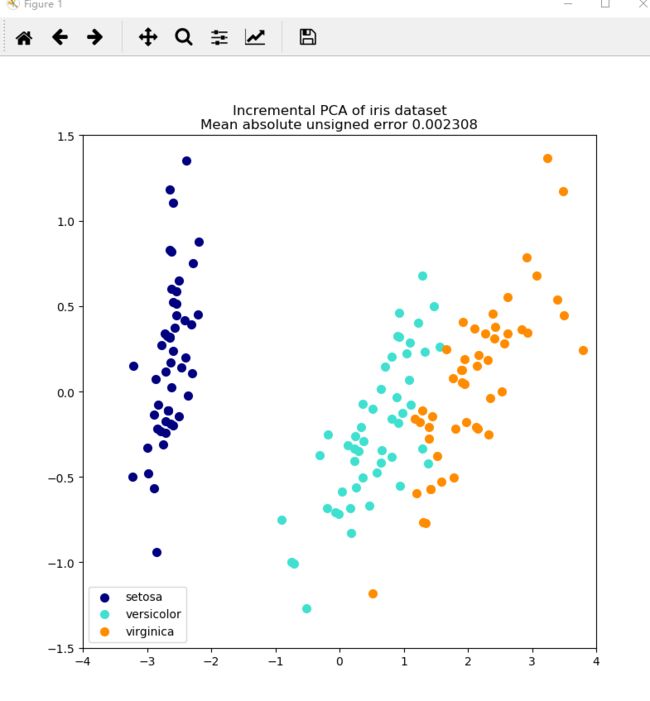
for x_transformed, title in [(x_ipca, "Incremental PCA"), (x_pca, "PCA")]:
plt.figure(figsize=(8,8))
for color,i,target_name in zip(colors,[0,1,2],iris.target_names):
plt.scatter(x_transformed[y==i,0],x_transformed[y==i,1],color=color,linewidths=2,label=target_name)#总过有三种,每一种的第一维作为x,第二维作为y
if "Incremental" in title:
err=np.abs(np.abs(x_pca)-np.abs(x_ipca)).mean()#求一下两者偏差并求其差值绝对值
plt.title(title + " of iris dataset\nMean absolute unsigned error "
"%.6f" % err)
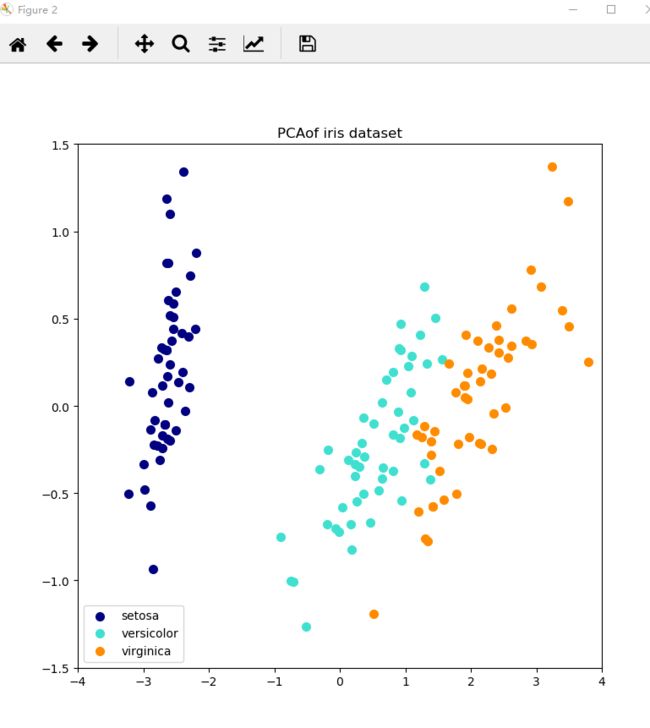
else:
plt.title(title+"of iris dataset")
plt.legend(loc="best",shadow=False,scatterpoints=1)
plt.axis([-4,4,-1.5,1.5])#四个参数用来设定x,y 轴的最大值和最小值
plt.show()
上述代码的结果展示:
至此,本系列已经暂时告一段落,经过这一系列的总结后,基本上对于机器学习的常用算法有了了解和简单应用,下一系列就是机器学习的强化实战项目