title: 统计学基础汇总
date: 2017-06-01 12:00:00
type: "tags"
tags:
- 数据描述
- 统计术语
categories:
- 生物统计
统计学术语
下面是一些常见的医学或生物学统计学术语。
数据和变量
在了解这两个术语之前,先看一组数据,从这组数据出发,说明这几个术语。
这组数据是R中自带的数据集,即iris这个数据集,iris数据集的中文名是安德森鸢尾花卉数据集,英文全称是Anderson’s Iris data set。iris包含150个样本,对应数据集的每行数据。每行数据包含每个样本的四个特征和样本的类别信息,所以iris数据集是一个150行5列的二维表,我们先看一下这个数据集的结构,如下所示:
> str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
再看一下前几条信息,如下所示:
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
从上面的这两个结果,我们可以得到这些信息:
第一,这个数据集一共有150行,5列。
第二,每1列的名称分别为Sepal.Length、Sepal.Width、Petal.Length、Petal.Width和Species,它们分别表示鸢尾花的花萼长度,花萼宽度、花瓣长度,花瓣宽度,种属,也就是说第1行中一共有这5个信息,我们把这5个信息称为变量(variable)。这里需要说明一下的是,变量(variable)在计算机/数据库等领域也叫属性(attribute)、特征(feature)、特性(characteristic)、字段(field)等等。
再回到iris这个数据集中。
其中,我们把种属(Species)这个信息称为定性变量(qualitative variable),定性变量取的值称为水平(level)或类(class)。定性变量有其它的教材中也会称为分类变量(categorical variable)、属性变量(attributives variable)、名义变量/标称变量(nominal variable)或维度(dimension)。
再看其它的4个变量,它们是用具体的数字表示,这些变量称为定量变量(quantitative variable),有也领域也称为指标。
定性变量的例子除了种属外,还有其他的例子,例如我们常见的性别,颜色等,在有些情况下,定量变量也会按照定性变量去处理,例如,为了调查方便,我们在问卷中可以只问高收入、中收入还是低收入,而不是问具体多少钱,这种定性变量还能进行排序,它们也常常称为定序变量(ordinal variable)。
定量变量还能分为连续型变量(continuous variable)和离散型变量(discrete variable)。
连续型变量的例子有身高、体重、热量、速度、长度等,它们的取值 是实数轴的某一个区间或者是某些区间集合中的所有可能点的变量。
离散型变量的例子有,某种事件发生的次数,例如抛5次硬币,在描述有几次正面朝上的时候,只可能是0次,1次,2次,3次,4次,5次,而不可能是1.5次这种小数,离散型变量只能取正整数或0。
还看上面的案例,整个iris这个数据集中,除了第1行的变量名称外,剩下的内容则是与这些变量对应的数据(data),可以把数据看成变量的观测值,或者是试验结果,例如,身高是一个变量,测量一个人的身高,就好比一次试验,可观测到一次试验结果,就是观测值(observation)。这里还要提一下,观测值(observation)在计算机/数据库领域也叫记录(record)、对象(object)、向量(vector)、模式(pattern)、事件(event)、例(case,instance)、样本(sample)、或项、实体(entity)等等。
我们一般所说的数据是一个集合名词,每一个数字包含很多观测值,每个观测值也称为一个数据点(data point, point)或例(case)。就以这个iris的数据集为例,它的每1列代表一个变量,而每1行则为一个对象关于各个变量的观测值,簇也把这种数据方阵的每一行叫做一个观测(值),就像下面的样子,它就是一个观测:
这也是一个观测值,如下所示:
横断面研究和纵贯研究
横断面研究(cross-sectional study)是指,它的数据是一群人在某个时间点的情况。
纵贯研究(longitudinal study)是指,在一段时间内手里观察同一群人。
概率和随机变量
在统计学研究中,有很多对象都被认为具有随机性(randomness),随机的事情也有规律的,例如我们抛一个硬币,在硬币落在地面之前,硬币朝哪面我们是不知道的,它是随机的,事先无法准确地预测。但是,只要这个硬币是正常的,没问题的,那么我们就知道,硬币朝上与朝下的概率基本上是相等的。
在这里,硬币的朝上与朝下的这个变量,它就是随机变量(random variable)。而一个随机变量的性质则完全被与其相关的概率或概率分布决定。那什么是概率?
一个事件(event)的概率(probability)是该事件发生可能性的一个数量度量,它的聚会范围是0到1,也可能是0或1.当一个事件的概率接近1时,则说明这个事件很可能发生;如果概率接近0,则说明不太可能发生,如果概率为0.5,那么说明该事件发生和不发生的可能性一样。
简单来说,概率称量某个事件出现的机会,有些概率在某种假定条件下可以算出来,例如抛硬币,得到正面朝上与反面朝上的概率都是0.5,这种可能计算概率的事件称为等可能事件(equally likely event),这种可能是假定的,对于硬币来说,就是假定正面与反面朝上的㜅一样,如果我们抛了一千次,其中得到正面与反面朝上的频率或相对频数(relative frequency)都接近0.5,那么就说明这个硬币是公平的,是正常的,这些事件理论上可能通过重复试验中出现的频率来计算其发生的概率。
不过有些概率是无法用重复计算来估计的,例如有人认为,最近3个月内中东地区发生大规模军事冲突的概率是80%,这显著无法用重复试剂来估计,这只是他们基于过去的经合和掌握的信息形成的信息,这种概率称为主观概率(subjective probability)。
利用R产生随机数
在进行抽样时,或者是模拟某个分布时,我们常常要用到随机数,现在都是用软件来生成随机数,虽然这种随机数不晃真正的随机数,但是已经足够使用了,使用软件生成的这种随机数称为伪随机数(pseudo-random number),现在介绍一下用R来如何生成随机数。
现在生成10个2到3之间的,服从均匀分布的伪随机数,如下所示:
> set.seed(1000)
> runif(10,2,3)
[1] 2.327879 2.758846 2.113936 2.690755 2.516402 2.067738 2.738715 2.583535
[9] 2.215771 2.256122
现在解释一下,先看runif()这个函数,在R中,这个函数前面的r表示随机,unif表示服从均匀分布,类似的还有rnorm(),它的功能类似,只是它生成的是服从正态分布的随机数,其中norm就是正态分布的意思。
现在,再看set.seed(1000)的作用是保证你随机生成的数字前后一致,如果它的参数就是一个数字,这个数字可以随意指定,括号里的数字只要一致,那么每次生成的随机数就一致,如果不使用这个函数,那么我们每次运行runif(10,2,3),它生成的随机数就不一样,现在看一下下面的代码:
> runif(10,2,3) # 不指定set.seed()
[1] 2.567518 2.049710 2.561620 2.966179 2.509945 2.700937 2.020349 2.783569
[9] 2.584397 2.317293
> runif(10,2,3) # 再次运行runif(10,2,3),生成的结果就不一样
[1] 2.996208 2.531047 2.109908 2.633212 2.797929 2.712990 2.702835 2.562833
[9] 2.258873 2.506937
> set.seed(1000) # 指定set.seed(1000)
> runif(10,2,3) # 生成的结果就与前面的一样
[1] 2.327879 2.758846 2.113936 2.690755 2.516402 2.067738 2.738715 2.583535
[9] 2.215771 2.256122
个体、总体、样本和抽样
为了说明这几个术语,我们还要看一个案例。
我们要调查一下外地游客在重庆认路的情况进行调查,那么我们可以这么设计问题,“请问,你在重庆旅游时,是否很容易找到目的地?”可能的回答有这些:“很容易”,“不容易“,”不知道“。调查的目的是希望知道在重庆的游客中,对这个问题的三种回答所占的比例,显然不可能调查所有的游客,但我们可以调查其中的一部分,进而估计出在重庆的所有游客的回答。
在这个例子中,单个游客称为调查的对象(object),他们的回答称为个体(element,或individual, unit),而所有在重庆的游客对这个问题的回答称为一个总体(population),总体是包含所有要研究的个体的集合,而调查时,问到那些游客则称为该总体的一个样本(sample),是总体中挑选出来的一部分。
在抽取样本时,如果总体中的每一个体都有同等机会被选到样本中,这种抽样称为简单随机抽样(sample random sampling),这样得到的样本称为随机样本(random sample)。不过即使是随机抽样,也不可能保证样本与总体的对应特征完全一样,会出现与总体的误差,这种误差无法避免,这样的误差称为抽样误差(sampling error)。
观察单位(observed unit)
观察单位也叫个体(individual),是统计研究中的基本单位,它可以是一个人,一头动物,也可能是特指一群人(例如一个家庭、一个幼儿园,一个自然村)。
总体(population)
根据研究目的而确定的同质观察单位的全体,更确切地说,它是同质的所有观察单位某种观察值的集合,例如调查某地2008年7岁正常女童的身高,而其中的观察单位(个体)则是每个女童。由于这里的总体明确规定了空间、时间、人群范围内有限个观察单位,因此称为有限总体(finite populaton)。而在一些情况下,总体的概念则是设想的或抽象的,例如研究某治疗慢性前列腺增生的药物的疗效,这里的总体的同质基础是慢性前列腺增生患者,该总体应包括用该药治疗的所有前列腺增生症患者的治疗结果,没有时间和空间的限制,其观察单位的全体数只是理论上存在的,因此可以视为“无限”,称为无限总体(infinite populaton)。
虽然我们要研究某个问题是关于整个总体的,但是研究者通常不可能考察总体中的所有个体,为了降低成本,因此在医学研究中通常彩从总体中抽取样本(sample)的方法,根据样本信息来推断总体特征,这种方法叫抽样研究(sampling research),从总体中抽取部分观察单位的过程称为抽样(sampling)。
为了保证样本的代表性,抽样必须遵循随机化(randomization)原则。从总体中随机抽得的部分观察单位,其实际测量的集合就是样本,该样本中包含的观察单位数称为该样本的样本含量(sample size)。例中从某地2008年7岁正常女童中,随机抽取了110名女童,测量身高,得到了110名女童的身高测量值,组成了样本;也可能从就诊的前列腺增生症患者中随机抽取了100名患者,并观察药物的治疗效果,就组成了治疗效果的样本。
变量(variable)
确定总体后,研究者对每个观察单位的某项特征进行观察或测量,这种特征能表现观察单位的变量异,就是变量。例如某地7岁女童的身高,体重都可以视为变量。
统计推断
在实际研究工作中,受条件所限,在研究中很难得到整个总体,往往堡垒有得到总体中的一个子集,即实际工作中往往按随机的方式从总体中抽取若干有代表性的同质个体所构成的一个样本(sample)进行研究,这就需要通过样本有限的、不确定的信息来歓有关总体的特征,这就是统计推断(statistical inference),简言之,统计推断是指由样本所提供的信息对总体数量规律做出推断。
强度相对数
说明某现象发生的频率或强度,称为率。常以百分率(%)、千分率(‰)、万分率(1/万)、十万分率(1/10万)等表示。
例5-1:2839名职工,发生高血压5人,高血压发病率为5/2839=1.76‰。
结构相对数
表示事物内部某一部分的个体数与该事物部分个体数的总和之比,用来说明各构成部分在总体中所占的比重或分布,称为构成比,通常以100%为比例基数。
例5-2 某医院1990年因五种疾病死亡的人数共190人,其中死于恶性肿瘤者58人,恶性肿瘤死亡人数占五种疾病死亡人数的构成比为58/190=30.53% 。
相对比
相对比简称比(ratio),是两个有关指标之比,说明两指标间的比例关系,通常以倍数或百分数(%)表示。例如某年医院出生婴儿中,男性为370,女性为358,则婴儿性别比为370/358*100=103
同比
发展速度主要是为了消除季节变动的影响,用以说明本期发展水平与去年同期发展水平对比而达到的相对发展速度。如,本期2月比去年2月,本期6月比去年6月等。其计算公式为:同比发展速度=本期发展水平/去年同期发展水平×100%。
环比
当前水平与前一时期水平之比,表明现象逐期的发展速度。如计算一年内各月与前一个月对比,即2月比1月,3月比2月,4月比3月 ……12月比11月,说明逐月的发展程度。
数据的描述
我们拿到一批数据,可能会考虑这些问题,这些数据是什么,这些数据如何表示,如何从整体上来描述这批数据。
如何查看数据
计量资料(measurement data)
计量资料又叫定量资料(quantitative data)或数值变量资料(numerical variable),表现为数值大小,一般有计量单位,例如身高多少厘米,体重多少公斤。根据测量值是否连续,又可分为连续型(continuous)和离散型(discrete),连续理革可在褛范围内聚任意值,例如身高,体重,而离散型只能取整数值,例如死亡人数。
离散型数据(discrete data)
离散型数据本质上是一种分类。最典型的例子,就是性别、种族、职业、教育程度等。在多数情况下,离散型数据并没有具体的数值(比如性别中的男和女),或者虽然形式上由数值表示,但数值本身并没有明确的意义(比如用邮政编码来记录受试者居住的地域)。有些离散变量是有某种顺序关系的,比如说教育程度可以从低到高排列,而有些离散变量并没有这种顺序,比如说某个基因的基因型。这两种情况分别称为有序变量(ordinal variable)和名义变量(nominal variable)。
连续型数据(continuous data)
连续型数据的数值有具体的科学意义,并且可以在数轴上的某个范围连续取值比如身高、体重、血糖浓度、肾小球滤过率等。
计数资料(enumeration data)
计数资料又称定性资料(qualitative data )或无序分类(unordered categorical variable)变量资料,亦称为名义变量资料,它的变量值是定性的,表现为互不相容的特性,例如结果的阴阳,家族史的有无等,分为两种:一种是二分类,例如治愈与未治愈,另一种是多分类,例如血型,A型,B型,AB型和O型。
等级资料(ranked data)
又称半定量资料(semi-quantitative data)或有序分类变量(ordinal categorical variable)资料:它将观察单位按某种程度分为等级,例如某药物治疗的效果为治愈、显效、好转、无效。
数据整体的一般描述
极差
又叫全距(Range),是用来表示统计资料中的变异量数(measures of variation),其最大值与最小值之间的差距;即最大值减最小值后所得之数据。
均值
通常情况下,我们所说的均值都是所有的数据之和除以数据的数目,但是,在一些特殊的情况下,会指明均值的类型,例如是算术均值,还是几何均值。
算术均值(arithmetic mean)
算术平均数是对集中趋势的最常用的描述。我们对某个量进行了n次观测,把测量到的数值分别记为X1, X2,…, Xn,那么要得到算术平均数,只需把X1到Xn加起来,再除以数据的个数n。数学公式为:
几何均值(geometric mean)
几何平均数是指n个观察值连乘积的n次方根。
中位数(median)
中位数是把该变量所有取值从小到大(或从大到小)排序,取最中间的一个(例如总共有21个数,则取排行第11的)。如果样本量是偶数,则取中间两个数的平均。
众数(mode)
一组数据中出现次数最多的数值,叫众数,有时众数在一组数中有好几个。用M表示。 理性理解:简单的说,就是一组数据中占比例最多的那个数。
例如:2,3,3,3,4,5的众数是3。 但是,如果有两个或两个以上个数出现次数都是最多的,那么这几个数都是这组数据的众数。 例如:2,2,3,3,4,5的众数是2和3。 其次,如果所有数据出现的次数都一样,那么这组数据没有众数。 例如:2,3,4,5没有众数。
百分位数(percentile)
如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数。可表示为:一组n个观测值按数值大小排列。如,处于p%位置的值称第p百分位数。
百分位数的计算
w<-c(75.0,64.0,47.4,66.9,62.2,62.2,58.7,63.5,66.6,64.0,57.0,69.0,56.9,50.0,72.0) # 建立向量w
quantile(w) # 给出w的四分位数
quantile(w,probs=seq(0,1,0.2),na.rm=FALSE) # 给出向量w的20%,40%分位数
quantile(w,0.80) # 求w的80%分位数
quantile(w,0.75)- quantile(w,0.25) #半极差计算
结果如下:
> quantile(w) # 给出w的四分位数
0% 25% 50% 75% 100%
47.40 57.85 63.50 66.75 75.00
> quantile(w,probs=seq(0,1,0.2),na.rm=FALSE) # 给出向量w的20%,40%分位数
0% 20% 40% 60% 80% 100%
47.40 56.98 62.20 64.00 67.32 75.00
> quantile(w,0.80) # 求w的80%分位数
80%
67.32
> quantile(w,0.75)- quantile(w,0.25) #半极差计算
75%
8.9
另外一种方法是用cumsum()函数来计算:
cumsum(round(table(w)/length(w)*100,2)) # cumsum表示的是累积之和
结果如下所示:
> cumsum(round(table(w)/length(w)*100,2)) # cumsum表示的是累积之和
47.4 50 56.9 57 58.7 62.2 63.5 64 66.6 66.9 69 72 75
6.67 13.34 20.01 26.68 33.35 46.68 53.35 66.68 73.35 80.02 86.69 93.36 100.03
四分位数(Quartile)
统计学中,把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。第一,四分位数 (Q1),又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。第二,四分位数 (Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。第三,四分位数 (Q3),又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。第三,四分位数与第一四分位数的差距又称四分位距(InterQuartile Range,IQR)。四分位距的优点在于,与全距(极差)相比,较少受异常值的影响。 R中用来显示四分位数的函数是quantile,另外用boxplot可以绘制出某个数据集的箱线图。
箱线图结果boxplot(w)如下所示:
条睛线图的解读:最下面是下界,最上面的圆圈是上界,上界的圆圈是异常值,中间矩形的底边是下分位数,上边是上四分位数,中间的粗线是中位数,箱体的高是四分位距。
数据离散程度的描述
对于一批数据来说,我们有时候需要看一下这批数据的波动分散程度如何,这就需要一些指标。
变异
医学研究的对象虽功能复杂的有机作整体。不同的个体在相同的条件下,对外因环境因素可以发生不同的反应,这种同质基础上个体特征值之间的差异,称为变异(variation)(医学统计学及SAS应用,王炳顺)。
离均差(deviation from the mean)
每一个变量值X与均数的差值,即离均差(X-)。
离均差平方和
由于离均差有正有负,最终所有离均差的和即为0,因此离均差的和无法描述一组数据的变异大小。因此将离均差平方后相加得到平方和,这就是离均差平方和(sum of squares of deviations from mean)。
总体方差
虽然离均差平方和消除了正负的影响,但是如果变量值N越大,则离均差平方和也越大,为此,将离均离平方和除以N就得到了方差,方差用表示,计算公式为:
另外,方差(variance)也称均方差(mean square deviation)
样本方差
上面的是总体方差,如果是样本方差,那么总体均值是未知的,因此,这个时候就要用样本的均值来替代总体的均值,这个时候也不能用来表示样本方差,需要用来表示方差,此外,N值也要减去1,公式就如下所示:
标准差
标准差(standard deviation)是方差的正平方根,其单位与原变量值的单位相同,总体标准差用表示,计算公式为:
为什么是N-1?
前面我们看到了总体方差与样本方差的分母不太一样,总体方差的分母是N,而样本方差则是N-1,为什么不一样呢?
在了解这个问题之前,我们先要了解一个统计学中的概念,自由度(degree of freedom)。
自由度的理解
这里的N严格意义上来讲,就是自由度,在统计学中,几乎所有的方法、所有指标都会涉及自由度,因为自由度跟样本的数目有关,任何统计学方法都离不开样本数目这个变量。自由度的字面意思是,计算样本统计量时能够自由取值的个数,一般用df来表示,来看一个简单的例子,如果有一个方程为x+y+z=100,一旦y和z的值固定,那么x的值也就固定了,因此x=100-y-z,因此,x,y,z这三个变量是不可能同时自由取值的,能够自由取值的个数只有2个,而不是3个,这就是说,自由度为2。
现在再来看一下样本的自由度为什么是N-1,因为我们在用样本统计量来估计总体参数时,我们有一个暗含的假定,即假定统计量是参数的无偏估计,也就是说样本的参数与总体的参数是相等的,这就相当于我们默认了一个限定(就像x+y+z=100一样),因此,样本的自由度就不是N,而是n-1。在不同的统计方法中,自由度都不一样,但基本原则都是每估计1个参数,就要降低一个自由度,现在看一下其他的统计学方法。
- 在单样本t检验中,自由度是t-1,因为只需要估计1个参数(均数),所以只需要消耗1个自由度,所以自由度是t-1.
- 在两组比较的t检验中,自由度是n1+n2-2,这是因为需要估计的参数有2个,也就是两组的均值,对于每一组而言,一旦均值固定,能够自由取值的个数就只有n1-1个(n1是第一组的例数),即自由度为n1-1。同样的道理,对于第二组而言,其自由度为n2-2,所以,总体自由度就是n1+n2-2。
- 在多组比较的方差分析中,当有k个组的时候,需要估计k值组的均数,所以总的自由度是(n1+n2+...nk)-k。而对于组间变异所用到的自由度,因为总均数是固定的,所以需要减去1个自由度,即k-1。
- 在回归分析中,如果有m个自变量,就有m个参数需要估计,而且还需要估计截距项,因此待估计的参数有m+a个(m个自变量加1个截矩项),所以模型的F检验用到的自由度为n-(m+1)。它意味着只剩下n-(m+1)个可以自由取值的数值来估计模型误差,当自变量数m固定时,如果样本n比较小,就会导致有效估计例数不足,从而导致结果不可靠。
因此,样本方差的分母使用n-1才更接近于总体的参数,这是无偏估计(unbiased estimator),如果直接使用n,那就是有偏估计(biased estimator ),不过当样本数量大到一定程度时,分母是n-1和n差别不大。
自由度这个角度是一种比较粗糙的理解方式,不过知乎上有人列出了证明过程,如下所示:
本来,按照定义,方差的估计值应时是这个:
,
但是这个估计是有偏的,因为:
接着,
而。所以,为了避免使用有偏的估计值,我们通常使用它的修正值,如下所示:,
样本标准差
样本标准差的公式如下所示:
标准差计算函数
在Excel中计算方差的公式为STDEV.P和STDEV.S其中,STDEV.P计算时,认为你给出的数据是总体,因此它的分母为N,而STDEV.S计算时,认为你给出的数据是样本,因此它的分母为N-1。在R中,用到的函数为sd,默认的就是样本,因此分母为N-1。
标准误与标准差的区别
在医学统计中,还经常遇到标准差与标准误。例如我们要调查地区A中10岁男孩的身高。如果全部都统计下来,直接测是最准确的数据。但是成本高,不现实。因此需要进行采样,一次测量100个男孩的身高,求这一次的均值M1与标准差S1,如果采样10次,每次都取100人,我们会得到10个均值,分别记为M1,M2,M3...M10,对这10个均值再求一个均值M以及标准差S,其中这个标准差S就是标准误(standard error),即均值的标准误差(standard error of mean)。
从上面的描述我们就知道了,标准差与标准误的区别在于:第一,标准差是对一次抽样的原始数据进行计算的,而标准误则是对多次抽样的样本统计量进行计算的(这个统计量可以是均值,可以是率);第二,标准差只是一个描述性指标,只是描述原始数据的波动情况,而标准误是跟统计推断有关的指标,大多数的统计量计算都需要用到标准误。
很多统计量都跟标准误有关,以简单的t检验为例,可能以前有的人都没有注意过。仔细观察一下就可以发现,t检验统计量的分子是两组样本数据的均值差值,反映了样本数据的差异;分母是标准误,反映了抽样误差。所以t检验反映了什么呢?其实就是看到底是抽样误差大还是真实差异大。如果分母的抽样误差大,那就说明结果可能不可靠,所以P值就会比较大;如果分子的差异大,说明抽样误差造成这种差异的可能性不大,所以P值就会比较小。
标准误与标准差的联系
SEM表示每次抽样获得的均数的标准差,因此如果要获取SEM,就必须做很多次抽样,这样也非常麻烦,但是标准误与标准差虽然不是一个概念,但在数学上有一定的联系,其公式如下所示:
变异系数(coefficient of variation)
简称为CV,标准差与均值的比值。公式为:
数据整体的呈现方式
箱线图和频率直方图
箱线图(boxplot)汇集了中位数、四分位差以及一些其他信息,能够使我们对样本的分布有一个直观的了解,也可以让我们快速发现数据中可能存在的错误(例如因为数据录入或单位错误导致的异常值)。它之所以被称为箱线图,是因为它用一个“箱子”来表示我们的数据中最靠中间的一半(即Q1和Q3之间的所有数据点),而用箱子上下的两根“胡须”来表示数据的上下限范围。箱线图的画法以及含义见下图。
正态分布
若随机变量X服从一个数学期望为、方差为的正态分布,记为。其概率密度函数为正态分布的期望值决定了其位置,其标准差决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布,即 = 0, = 1的正态分布,其公式为:
医学参考值
医学参考值(reference value)是指包括约大多数正常人的人体形态、功能和代谢产物等各种生理及生化指标常数,也称正常值。由于存在个体差异,生物医学数据并非常数而是在一定范围内波动,帮采用学参考值范围(medical reference range)作为判定正常和异常的参考标准。
医学参考值范围涉及采用单侧界值还是双侧界值的问题,这通常是依据医学专业知识而定,例如课本(医学统计学,孙振球,第四版)中的例2-1的红细胞数无论过低或过高均属异常,就采用双侧参考值范围制定下侧和上侧界值;血清转氨酶仅过高异常,应采用单侧参考值范围制定上侧界值;肺活量仅过低异常,就采用单侧参考值范围制定下侧界值。医学上常用的参考值范围有90%,95%,99%等,其中95%最常用。
其中确定参考值的方法通常有两种,分别为正态分布法和百分位数法。
正态分布法
对于服从正态分布的医学数据,可采用正态分布法计算参考值的范围,其计和公式为:
双侧1-参考值范围为:
单侧1-的参考值范围为:。
其中为无数,S为标准差,值可以查表得到。
案例:现在我们计算课本[^1]例2-1的资料估计正常成年女子的红细胞数的95%的参考值范围。计算结果如下所示:
raw_data <- read.csv("https://raw.githubusercontent.com/20170505a/raw_data/master/data_szq_201.csv") #导入数据
extract_data <- raw_data[,1] # 提取第一列数据
sd1 <- sd(extract_data)
mean1 <- mean(extract_data)
mean1 - 1.96*sd1 # 参考值的下限
mean1 + 1.96*sd1 # 参考值的上限
因此参考值的范围为3.353299,5.104657。
百分位数法
偏态分布资料医学参考值范围的制定通常采用百分位数法,所要求的样本含量比正态分布法要多(不低于100),其计算公式为:
双侧参透值范围为:
单侧参透值范围为:或
案例:课本无原始数据,此题略过。
数据描述的练习
例题2-1的描述性统计
(医学统计学.第四版.孙振球)
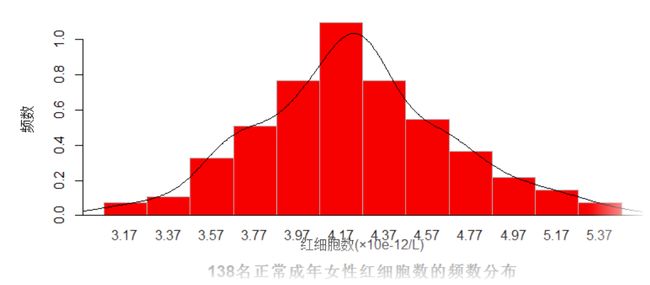
某医院用随机抽样方法检查了138名正常成年女子的红细胞数 ,其测量结果如下,试编制频数分布表。
raw_data <- read.csv("https://raw.githubusercontent.com/20170505a/raw_data/master/data_szq_201.csv")
#导入数据
extract_data <- raw_data[,1]
# 提取第一列数据
library(reshape2)
breaks<-seq(from = 3.07, to = 5.47, by = 0.2)
# 产生各个组距
data_table<-cut(extract_data,breaks=breaks,right=FALSE)
#分组,right=FALSE表示左闭右开
library(reshape2)
#载入reshape2包,使用其中的melt函数
melt(table(data_table))
#查看频数分布
middle_data<-c()
#求组中值,组中值从表中可以看出来就是区间两边的数的平均数
for(i in seq(1,12)){
middle <- (breaks[i]+breaks[i+1])*0.5
middle_data<-append(middle_data,middle)
}
# 绘图表
hist(extract_data,breaks,
right=FALSE,main="",
xlab="",ylab="频数",
axes=FALSE,
border="grey",
col="red",freq=F)
#data为数据集,breaks则是分组依据,right=FALSE则是左开右闭,xlab,ylab控制坐标
lines(density(extract_data))
#加入概率密度曲线
title(xlab="红细胞数(×10e-12/L)",line=0.8)
#加x轴的标题,往下超过x轴垂直距离为0.8个行距
text(4.5,-2.8,"-12",cex=0.5)
mtext("138名正常成年女性红细胞数的频数分布",1,line=2.5,cex=1.2,font=2)
#加主标题,1表示为下方
# line=2.5表示超过x轴垂直距离为2.5个行距
# cex为字体扩大倍数
# font=2表示加粗
abline(h=0)
#绘制y=0的线段,用此线表示x轴
axis(1,at=middle_data,tick=FALSE,pos=0.03)
# 绘制x轴,坐标为middle_data
# tick=FALSE表示坐标刻度不绘出,pos=1表示坐标轴在y=1处
axis(2)
#绘制y轴
频数分布如下:
> melt(table(data_table)) #查看频数分布
data_table value
1 [3.07,3.27) 2
2 [3.27,3.47) 3
3 [3.47,3.67) 9
4 [3.67,3.87) 14
5 [3.87,4.07) 22
6 [4.07,4.27) 30
7 [4.27,4.47) 21
8 [4.47,4.67) 15
9 [4.67,4.87) 10
10 [4.87,5.07) 6
11 [5.07,5.27) 4
12 [5.27,5.47) 2
图表如下所示
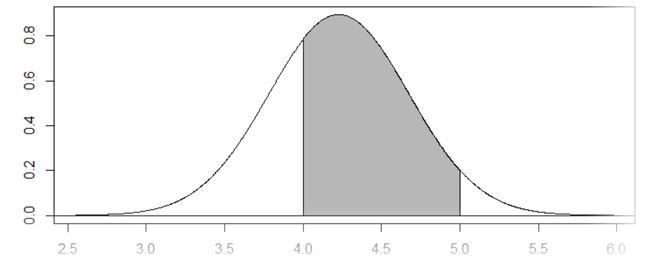
对例2-1,例2-2和例2-14已计算出某医院随机抽查的138名成年女子的红细胞数均数 ,标准差 。试估计该医院所抽查成年女子的红细胞数:①在4.0 以下者占成年女子总人数的百分比;②在4.00~5.00 之间者占成年女子总人数的百分比;③在5.00 以上者占成年女子总人数的百分比。
计算过程如下:
mean.data <- mean(extract_data)
sd.data <- sd(extract_data)
pnorm((4-mean.data)/sd.data) # 4.0以下的百分比
pnorm((5-mean.data)/sd.data) #5.0以下的百分比
1-pnorm((5-mean.data)/sd.data) #5.0以上的百分比
pnorm((5-mean.data)/sd.data)-pnorm((4-mean.data)/sd.data) #在4.00~5.00 之间的百分比
#或者是:
pnorm(5,mean(data),sd(data))-pnorm(4,mean(data),sd(data))
# 绘制数据集的正态分布图
x <- seq(min(extract_data)-0.52,max(extract_data)+0.52,length=1000)
y <- dnorm(x,mean(extract_data),sd(extract_data))
r1 <- 4
r2 <- 5
x2 <- c(r1,r1,x[xr1],r2,r2)
y2=c(0,dnorm(c(r1,x[xr1],r2),mean(data),sd(data)),0)
plot(x,y,type="l",xlab="",ylab="",lty=1)
abline(0,0)
polygon(x2,y2,col="grey")
结果如下所示:
[1] 0.3041459
> pnorm((5-mean.data)/sd.data) #5.0以下的百分比
[1] 0.9578038
> 1-pnorm((5-mean.data)/sd.data) #5.0以上的百分比
[1] 0.04219616
> pnorm((5-mean.data)/sd.data)-pnorm((4-mean.data)/sd.data) #在4.00~5.00 之间的百分比
[1] 0.653658
> pnorm(5,mean(data),sd(data))-pnorm(4,mean(data),sd(data))
[1] 0.6532998
结果与书中的不太一样,但结果接近,我估计是因为书中是查表,用的是近似值,R中的比较精确
数据的正态分布图如下所示:
例2-4:几何均数
某地5例微丝蚴血症患者治疗7年后用间接荧光抗体试验没得某抗体满意度例数分别为10,20,40,40,160,求几何均数。
data24<-c(10,20,40,40,160)
exp(mean(log(data24)))
结果如下:
> data24
[1] 10 20 40 40 160
> exp(mean(log(data24)))
[1] 34.82202
例2-5 平均抗体滴度
69例风湿关节炎(RA)患者血清EBV-VCA-IgG抗体满意度的分布,求其平均抗体滴度。
data25<-c(10,40,80,160,160,320,640,640,10,40,80,160,160,320,640,640,
10,40,80,160,320,320,640,640,10,40,80,160,320,320,640,640,20,40,80,
160,320,320,640,1280,20,40,80,160,320,320,640,1280,20,40,80,160,320,
320,640,40,40,80,160,320,320,640,40,80,80,160,320,640,640)
x <- table(data25)
x <- data.frame(x)
x$countdown <- as.numeric(levels(x$data25))
x$lgX <- round(log10(x$countdown),4)
x$flgX <- round(x$Freq*x$lgX,4)
结果为:
> x
data25 Freq countdown lgX flgX
1 10 4 10 1.0000 4.0000
2 20 3 20 1.3010 3.9030
3 40 10 40 1.6021 16.0210
4 80 10 80 1.9031 19.0310
5 160 11 160 2.2041 24.2451
6 320 15 320 2.5051 37.5765
7 640 14 640 2.8062 39.2868
8 1280 2 1280 3.1072 6.2144
上述结果是书中的频数表,与R的计算关系不大,在R中可以直接计算,如下
> exp(mean(log(data25)))
[1] 150.6411
例2-6 中位数
7名病人患某病的潜伏期分别为2,3,4,5,6,9,16天,求其中位数。
> data26<-c(2,3,4,5,6,9,16)
> median(data26)
[1] 5
例2-11:均数和极差
试计算下面三组同龄男孩的身高 均数和极差。
range.f <- function (x) (max(x)-min(x))
甲组 <- c(90,95,100,105,110)
乙组 <- c(96,98,100,102,104)
丙组 <- c(96,99,100,101,104)
range.f(甲组)
mean(甲组)
range.f(乙组)
mean(乙组)
range.f(丙组)
mean(丙组)
结果如下所示:
> range.f(甲组)
[1] 20
> mean(甲组)
[1] 100
> range.f(乙组)
[1] 8
> mean(乙组)
[1] 100
> range.f(丙组)
[1] 8
> mean(丙组)
[1] 100
参考资料
- 医学统计学.第四版.孙振球
- 小白统计.冯国双
- 为什么样本方差(sample variance)的分母是 n-1?
- 统计思维:程序员数学之概率统计.作者: Allen B.Downey,译者: 张建锋 / 陈钢 出版社: 人民邮电出版社