众数回归R语言包 modalreg

众数回归R语言包 modalreg

1 简介

主要功能为实现众数回归， 包括参数与非参数模型，提供自动带宽选择，模型预测与模型评估。
模型方法包括：
(1) 线性众数模型linear ¹
(2) 非参数B样条众数回归模型 bmr ²
(3) 非参数局部多项式众数回归模型 lmr ³
(4) 非参数核方法众数回归模型 kmr ⁴

两种交叉验证的带宽选择方法：
(1) 基于最优预测覆盖率 predict ²
(2) 基于最小二乘准则 mse ²

2 使用方法

1 打开Rstudio或R
2 该包的源文件存放在github中，要借助包管理工具devtools包，如果没有安装devtools，首先安装并加载devtools

install.packages(devtools)
library(devtools)

3 安装modalreg包

install_github("yuanwanli1995/modalregression/modalreg") 

4 加载modalreg
以上步骤只要第一次使用时需要，安装完成后，每次只需要加载。

library(modalreg)

3 使用介绍

3.1 模型训练

模型训练函数modalreg(x_train, y_train, method, bandwidth_criterion, hyperparameter，interval1，interval2)
参数解释

参数	含义	是否必选	类型	备注
x_train	训练数据自变量	必需	data.fram()	n*d
x_train	训练数据因变量	必需	data.fram()	n*1
method	回归函数形式	可选，默认B样条	“linear”, “bmr”, “lmr”, “kmr”	“linear"支持多元，后三种非参数模型仅支持一元回归
hyperparameter	超参数	可选，默认自动选择	长度为2的向量，如c(1,1)	第一个为控制众数模型稳健性超参数，第二个为函数光滑性参数
bandwidth_criterion	超参数选择方法	可选，默认"mse"	“predict”,"mse”	给定hyperparameter后，带宽选择方法失效
interval1	第一个参数搜索区间	可选，默认seq(0.05,1,0.05)	向量	如seq(0, 2,0.5)
interval2	第二个参数搜索区间	可选，默认seq(0.05,1,0.05)	向量	如seq(0, 2,0.5)

示例
为了方便模拟实验，modalreg内置一个模拟数据生成方法datagenerater(n,e,f) ,假定数据来自以下模型
$$Y=f(X)+ϵ$$

n 生成数据样本量
e 生成数据噪声类型， “gauss”， “mixgauss”，“mixgausssymmetry”，“cauchy”，“gamma”，"beta"五种
f 为函数类型, 可选 “quodratic”，“exp”，“log”，“sin”，“mexicohat”，“linear” 五种

datagenerater函数返回一个列表， 列表第一项是自变量，第二项为因变量，类型为数据框data.frame.

data<- datagenerater(200,"gamma","exp")
x_train<-data$x
y_train<-data$y
bmr1<-modalreg(x_train = x_train, y_train = y_train, method="bmr", hyperparameters=c(2,1)) # 给定超参数
bmr2<-modalreg(x_train = x_train, y_train = y_train, method="bmr",bandwidth_criterion="predict") #给定选择准则
bmr3<-modalreg(x_train = x_train, y_train = y_train, method="bmr",bandwidth_criterion="predict",
               interval1=seq(1,10,1), interval2 = seq(0,1,0.5)) # 给定超参数搜索区间 
kmr1<-modalreg(x_train = x_train, y_train = y_train, method="kmr",bandwidth_criterion="mse",
               interval1=seq(1,10,1), interval2 = seq(0,1,0.5)) # 使用kmr方法 
lmr1<-modalreg(x_train = x_train, y_train = y_train, method="kmr",bandwidth_criterion="mse")# 使用lmr方法 

3.2 模型查看

模型查看函数 modal.summray() , 可显示模型的训练结果，包括模型训练样本个数、维度、回归函数形式、最优超参数、回归系数、 训练迭代次数、训练集mean absolute error以及训练时间。

> modal.summary(bmr1)
n: 200          d: 1 
method: bmr 
hyperparameters: 2 1 
coefficients: 8.130762 6.39536 -0.552399 0.4161437 7.378951 
iterations: 12 
mean abslute error: 0.860825 
computing time: 0.02 s 

> modal.summary(bmr2)
n: 200          d: 1 
method: bmr 
hyperparameters: 1 0.1 
coefficients: 8.426918 6.200775 -0.857361 0.431175 7.107775 
iterations: 25 
mean abslute error: 0.8618467 
computing time: 10.97 s  # 需要搜索的训练过程计算时间更多

> modal.summary(bmr3)
n: 200          d: 1 
method: bmr 
hyperparameters: 10 0.5 
coefficients: 8.094925 6.416691 0.02215972 0.1074252 7.807926 
iterations: 5 
mean abslute error: 0.8862554 
computing time: 0.47 s 

> modal.summary(kmr1)
n: 200          d: 1 
method: kmr 
hyperparameters: 10 0.5 
coefficients: 0.1354988 0.1323728 0.1323279 0.1288853 0.1263787   ...  # 核方法有n个系数， 系数的解释性不强，只展示前五个
iterations: 5 
mean abslute error: 0.8519081 
computing time: 12.59 s  

> modal.summary(lmr1)
n: 200          d: 1 
method: lmr 
hyperparameters: 1 0.1 
coefficients: NaN 
iterations: 4917 
mean abslute error: 0.7542259 
computing time: 882.86 s # lmr非常耗时 

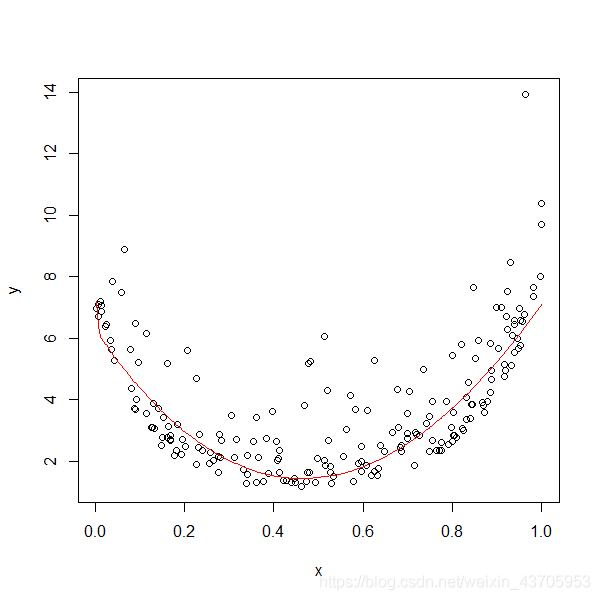
3.3 训练效果可视化

训练集拟合值可以使用modal.plot()查看

modal.plot(bmr1) 

3.4 模型预测

模型预测函数modalpredict(model, x_predict) , model为训练的mr模型， x_predict为预测数据，必须与x_train维度相同，类型为数据框。

pred<-modalpredict(bmr1, x_train)
plot(x_train, y_train)
lines(x_train,pred,col="red")

---

1. Yao W, Li L. A new regression model: modal linear regression[J]. Scandinavian Journal of Statistics, 2014, 41(3): 656-671. ↩︎

2. 袁万里, 杨联强, 王学军. 基于B样条的众数回归模型[J]. 系统科学与数学 ,\ 2020, 40(11):2125-2135. ↩︎ ↩︎ ↩︎

3. Yao W, Lindsay B G, Li R. Local modal regression[J]. Journal of nonparametric statistics, 2012, 24(3): 647-663. ↩︎

4. Feng Y, Fan J, Suykens J A K. A Statistical Learning Approach to Modal Regression[J]. Journal of Machine Learning Research, 2020, 21(2): 1-35. ↩︎