int型溢出问题

问题

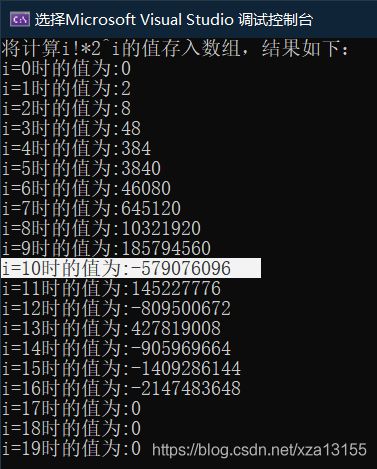
在执行乘法时（$i!\ast 2^i,(i=0,1,...,n-1)$），当计算的值超过了int上限后却变成了负数。

原理

奇怪的循环

int的范围是：-2147483648~2147483647
如果超出这个范围会出现循环；也就是最大的数+1变成了最小的数，最小的数-1又成了最大的数。所有的数就像模运算一样形成了循环。
如:-2147483648-1=2147483647;2147483647+1=-2147483648
可以看到在INT_MAX后做累加，就回到了INT_MIN。

计算机的编码

对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式。上面的循环就是计算机采用的特殊编码造成的。下面分别做介绍。

1，原码
一开始人们是通过原码来表示整数，整数有正负之分，便通过符号位+二进制的方式表示。（最高位（最左边）取0表示正数，取1表示负数。然后加上对应的二进制。）
+1 = 0000 0001
-1 = 1000 0001

2，反码
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反

3，补码
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补

4，为何选择补码
现代的计算机底层是采用补码来对整数编码。这是因为补码能够极大的简化运算。
对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单.。于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.

使用原码和反码让符号位也参与计算,都会产生错误
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2

1 - 1 = 1 + (-1) = [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

而使用补码则不会有这个问题
1-1 = 1 + (-1) = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=0

此外使用补码还能多表示一个负数
0用[0000 0000]表示, 而以前出现问题的-0则不存在了.可以用[1000 0000]表示-128.
这就是为什么现在32位的int范围是-2147483648~2147483647

循环的产生

INT的最大值2147483647的二进制是：
1111111111111111111111111111111
2147483648的二进制是：
10000000000000000000000000000000

换成补码：
0 00000000000000000000000000000000（INTMAX)
0 0111111111111111111111111111111111111(INTMAX+1，溢出了1位)

因为INT只支持32位，就多出来了1位，计算机默认会截除掉最高位（最左边）。
则INTMAX+1的补码就变成了：
0 111111111111111111111111111111111111=-2147483647

计算机巧妙的利用这一点在溢出后达成了一个循环

如何识别溢出

乘法

设int a, b;
ab>INTMAX 显然是无法判断出结果的（溢出了就从负数开始循环）。
换个思路使用b>INTMAX/a
就是把溢出的ab拆分为未溢出的a和b，然后执行除法来判断是否溢出。
本问题的判断就可以修改如下：

int algo(int n, int a[])
{
     
	a[0] = 0;
	a[1] = 2;
	for (int i = 2; i < n; i++)
	{
     
		a[i] = 2 * i * a[i - 1];
		//if (a[i-1] > INT_MAX / (2*i))
		if(0)
		{
     
			printf("a[i]:%d\n", i);
			printf("堆栈上溢，按出错处理！");
			exit(OVERFLOW);
		}
	}
	return OK;
}

加法

例：检查两个非负整型变量a+b是否溢出
第一种：if(a+b < 0)
这种做法是检查内部寄存器的标志位是否为负

第二种： if((unsigned)a +(unsigned)b >INT_MAX)
这种做法是强制将a和b都强制转换成无符号整数

第三种： if(a > INT_MAX - b)
这种做法不需要用到无符号算术运算符，也和我们之前乘法的处理类似

参考文献

[1]https://blog.csdn.net/weixin_33898233/article/details/92355647.
[2]https://blog.csdn.net/shun_smile/article/details/80042210.
[3]https://blog.csdn.net/zl10086111/article/details/80907428.
[4]https://zhuanlan.zhihu.com/p/340095782.
[5]https://blog.csdn.net/WmxL56/article/details/38380627.