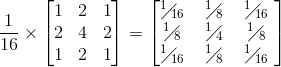基于matlab的传统算法图像去噪的实现原理

题目要求：图像去噪

      下面是一幅噪声图像，请设计图像去噪方案，计算去噪图像与原始图像的PSNR（峰值信噪比）、SSIM（结构相似性）指标。

PSNR（峰值信噪比）：是最普遍和使用最为广泛的一种图像客观评价指标，然而它是基于对应像素点间的误差，即基于误差敏感的图像质量评价。由于并未考虑到人眼的视觉特性（人眼对空间频率较低的对比差异敏感度较高，人眼对亮度对比差异的敏感度较色度高，人眼对一个区域的感知结果会受到其周围邻近区域的影响等），因而经常出现评价结果与人的主观感觉不一致的情况。（PSNR的单位是dB，数值越大表示失真越小。）

SSIM（结构相似性）：是一种全参考的图像质量评价指标，它分别从亮度、对比度、结构三方面度量图像相似性。（SSIM取值范围[0,1]，值越大，表示图像失真越小。）

1.什么是图像噪声

图像噪声是指存在于图像数据中的不必要的或多余的干扰信息。 图像中各种妨碍人们对其信息接受的因素即可称为图像噪声 。噪声在理论上可以定义为“不可预测，只能用概率统计方法来认识的随机误差”（图像噪声可以描述成不同的类型，其归类方法就是基于统计方法的）。因此将图像噪声看成是多维随机过程是合适的，因而描述噪声的方法完全可以借用随机过程的描述，即用其概率分布函数和概率密度分布函数。通俗的说就是噪声让图像不清楚。

2. 图像噪声来源

a、图像获取过程中

图像传感器CCD和CMOS采集图像过程中受传感器材料属性、工作环境、电子元器件和电路结构等影响，会引入各种噪声。

b、图像信号传输过程中

传输介质和记录设备等的不完善，数字图像在其传输记录过程中往往会受到多种噪声的污染。

3. 噪声分类

噪声按照不同的分类标准可以有不同的分类形式：

• 基于产生原因：内部噪声，外部噪声。
• 基于噪声与信号的关系：

加性噪声：加性噪声和图像信号强度是不相关的，这类带有噪声的图像g可看成为理想无噪声图像f与噪声n之和：

                                                                             g = f + n；

乘性嗓声：乘性噪声和图像信号是相关的，往往随图像信号的变化而变化，载送每一个象素信息的载体的变化而产生的噪声受信息本身调制。在某些情况下，如信号变化很小，噪声也不大。为了分析处理方便，常常将乘性噪声近似认为是加性噪声，而且总是假定信号和噪声是互相统计独立。

                                                                               g = f + f*n

• 按照基于统计后的概率密度函数：

是比较重要的，主要因为引入数学模型这就有助于运用数学手段去除噪声。在不同场景下噪声的施加方式都不同，由于在外界的某种条件下，噪声下图像-原图像（没有噪声时）的概率密度函数（统计结果）服从某种分布函数，那么就把它归类为相应的噪声。下面将具体说明基于统计后的概率密度函数的噪声分类及其消除方式。

4.图像去噪算法的分类

空间域滤波

空域滤波是在原图像上直接进行数据运算，对像素的灰度值进行处理。常见的空间域图像去噪算法有邻域平均法、中值滤波、低通滤波等。

 

变换域滤波

图像变换域去噪方法是对图像进行某种变换，将图像从空间域转换到变换域，再对变换域中的变换系数进行处理，再进行反变换将图像从变换域转换到空间域来达到去除图像嗓声的目的。将图像从空间域转换到变换域的变换方法很多，如傅立叶变换、沃尔什-哈达玛变换、余弦变换、K-L变换以及小波变换等。而傅立叶变换和小波变换则是常见的用于图像去噪的变换方法。

偏微分方程

偏微分方程是近年来兴起的一种图像处理方法，主要针对低层图像处理并取得了很好的效果。偏微分方程具有各向异性的特点，应用在图像去噪中，可以在去除噪声的同时，很好的保持边缘。偏微分方程的应用主要可以分为两类:一种是基本的迭代格式，通过随时间变化的更新，使得图像向所要得到的效果逐渐逼近，这种算法的代表为Perona和Malik的方程，以及对其改进后的后续工作。该方法在确定扩散系数时有很大的选择空间，在前向扩散的同时具有后向扩散的功能，所以，具有平滑图像和将边缘尖锐化的能力。偏微分方程在低噪声密度的图像处理中取得了较好的效果，但是在处理高噪声密度图像时去噪效果不好，而且处理时间明显高出许多。

变分法

另一种利用数学进行图像去噪方法是基于变分法的思想，确定图像的能量函数，通过对能量函数的最小化工作，使得图像达到平滑状态，现在得到广泛应用的全变分TV模型就是这一类。这类方法的关键是找到合适的能量方程，保证演化的稳定性，获得理想的结果。

形态学噪声滤除器将开与闭结合可用来滤除噪声，首先对有噪声图像进行开运算，可选择结构要素矩阵比噪声尺寸大，因而开运算的结果是将背景噪声去除；再对前一步得到的图像进行闭运算，将图像上的噪声去掉。据此可知，此方法适用的图像类型是图像中的对象尺寸都比较大，且没有微小细节，对这类图像除噪效果会较好。

5.图像去噪

5.1均值滤波：

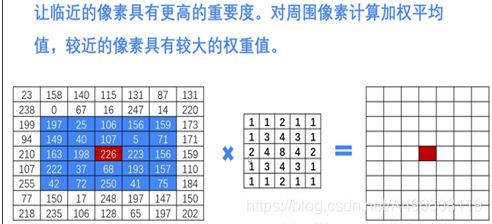
       均值滤波是指任意一点的像素值，都是周围   个像素值的均值。例如下图中，红色点的像素值是其周围蓝色背景区域像素值之和除25，25=5 5 是蓝色区域的大小。

均值滤波详细的计算方法如下图所示：

 

其中5 5的矩阵称为核，针对原始图像内的像素点，采用核进行处理，得到结果图像，如下图所示

 

5.2中值滤波：

       在使用邻域平均法去噪的同时也使得边界变得模糊。而中值滤波是非线性的图像处理方法，在去噪的同时可以兼顾到边界信息的保留。选一个含有奇数点的窗口 ，将这个窗口在图像上扫描，把窗口中所含的像素点按灰度级的升或降序排列，取位于中间的灰度值来代替该点的灰度值。计算过程如下图所示：

5.3高斯滤波：

为了克服简单局部平均法的弊端(图像模糊)，目前已提出许多保持边缘、细节的局部平滑算法。它们的出发点都集中在如何选择邻域的大小、形状和方向、参数加平均及邻域各店的权重系数等。

图像高斯平滑也是邻域平均的思想对图像进行平滑的一种方法，在图像高斯平滑中，对图像进行平均时，不同位置的像素被赋予了不同的权重。高斯平滑与简单平滑不同，它在对邻域内像素进行平均时，给予不同位置的像素不同的权值，下图的所示的 3 3 和 5 5 邻域的高斯模板。

（1）核大小为 3 3

（1）核大小为 5 5

高斯滤波让临近的像素具有更高的重要度，对周围像素计算加权平均值，较近的像素具有较大的权重值。如下图所示，中心位置权重最高为0.4。

5.4维纳滤波：

     维纳滤波（wiener filtering) 一种基于最小均方误差准则、对平稳过程的最优估计器。这种滤波器的输出与期望输出之间的均方误差为最小，因此，它是一个最佳滤波系统。它可用于提取被平稳噪声所污染的信号。

5.5小波滤波：

随着小波理论的日益完善，其以自身良好的时频特性在图像去噪领域受到越来越多的关注，开辟了用非线性方法去噪的先河。具体来说，小波能够去噪主要得益于小波变换有如下特点：

（1）低熵性。小波系数的稀疏分布，使图像变换后的熵降低。 意思是对信号（即图像）进行分解后，有更多小波基系数趋于0（噪声），而信号主要部分多集中于某些小波基，采用阈值去噪可以更好的保留原始信号。

（2）多分辨率特性。由于采用了多分辨方法，所以可以非常好地刻画信号的非平稳性，如突变和断点等（例如0-1突变是傅里叶变化无法合理表示的），可以在不同分辨率下根据信号和噪声的分布来消除噪声。

（3）去相关性。小波变换可对信号去相关，且噪声在变换后有白化趋势，所以小波域比时域更利于去噪。

（4）基函数选择灵活。小波变换可灵活选择基函数，也可根据信号特点和去噪要求选择多带小波和小波包等（小波包对高频信号再次分解，可提高时频分辨率），对不同场合，选择不同小波基函数。  

根据基于小波系数处理方式的不同，常见去噪方法可分为三类：

（1）基于小波变换模极大值去噪（信号与噪声模极大值在小波变换下会呈现不同变化趋势）

（2）基于相邻尺度小波系数相关性去噪（噪声在小波变换的各尺度间无明显相关性，信号则相反）

（3）基于小波变换阈值去噪

小波去噪实现步骤：

（1）二维信号的小波分解。选择一个小波和小波分解的层次N，然后计算信号s到第N层的分解。

（2）对高频系数进行阈值量化。对于从1~N的每一层，选择一个阈值，并对这一层的高频系数进行软阈值量化处理。

（3）二维小波重构。根据小波分解的第N层的低频系数和经过修改的从第一层到第N的各层高频系数，计算二维信号的小波重构

5.6 非均值局部滤波(NL-means)：

非局部均值（NL-means）是近年来提出的一项新型的去噪技术。该方法充分利用了图像中的冗余信息，在去噪的同时能最大程度地保持图像的细节特征。基本思想是：当前像素的估计值由图像中与它具有相似邻域结构的像素加权平均得到。

非局部均值去噪算法其实很简单，该种去噪方法和高斯去噪和双边滤波器去噪很像，都是利用一些准则，通过“周围”的像素点加权估计像素点的真实值，如下图所示：

最左边一副图表示Gauss滤波的特点，就是利用图像像素点相近的程度来估计权重，中间幅图表示双边滤波器在考虑像素点本身取值的相近性以外，还考虑了相近像素点与被估计的像素点的距离，如果离被估计的像素点越近将具有更高的权重，非局部均值则是在一个窗口中搜索相近的图像块来进行权重分配（如绿色的框内的区域为搜索的区域，黄色的窗口为搜索的图像块，深褐色的窗口中的中心点为需要去噪的点，通过加权的形式将最相近的几个像素块中的中心点结合起来估计真实值。

5.7 小波与非均值局部混合滤波：

NL-means去噪算法使用的是相近的图像块来进行权重分配，而小波变换使用的则是图像块内相关进行权重分配。这两种方法都取得了不错的效果，一个很自然的想法就是：可以同时使用他们两个方法吗？效果怎么样呢？

实现步骤：

1. 先对原噪声图像进行小波除噪。
2. 对小波除噪完的图像进行非均值局部滤波。均值、中值、高斯、维纳、小波、NL-means的图像去噪的matlab程序：https://blog.csdn.net/A496608119/article/details/110688516