DBSCAN密度聚类算法及python实现

DBSCAN

DBSCAN(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法，和K-Means，BIRCH这些一般只适用于凸样本集的聚类相比，DBSCAN既可以适用于凸样本集，也可以适用于非凸样本集。

密度聚类原理

密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间的紧密相连的。通过将紧密相连的样本划为一类，这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别，则我们就得到了最终的所有聚类类别结果。

 

DBSCAN定义

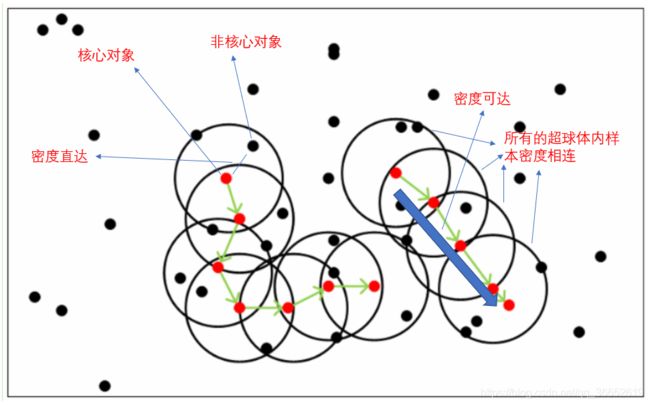
DBSCAN是基于一组邻域来描述样本集的紧密程度的，参数(ϵ, MinPts)用来描述邻域的样本分布紧密程度。其中，ϵ描述了某一样本的邻域距离阈值，MinPts描述了某一样本的距离为ϵ的邻域中样本个数的阈值。

图中MinPts=5，红色的点都是核心对象，因为其ϵ-邻域至少有5个样本。黑色的样本是非核心对象。所有核心对象密度直达的样本在以红色核心对象为中心的超球体内，如果不在超球体内，则不能密度直达。图中用绿色箭头连起来的核心对象组成了密度可达的样本序列。在这些密度可达的样本序列的ϵ-邻域内所有的样本相互都是密度相连的。

假设样本集：

引入几个概念：

 

ϵ-邻域：

对于  , 其ϵ邻域包含样本集D中与xj的距离不大于ϵ的子样本集，即 ，

子样本集的个数记为

（ϵ相当与一个半径，好比上图的圆的区域）

核心对象：

这个概念很简单，就是对于任一 , 它的ϵ-邻域对应  至少包含MinPts个样本的话 就是核心对象，也就是上图中的红色的点。

密度直达：

若 在   的ϵ-邻域 内的话，并且  是核心对象， 称为  由  密度直达。反之不一定成立除非也是核心对象。

密度可达：

 对于  和  存在这样的样本序列：, 并且满足， , 。

若   由   密度直达，  则   由   密度可达，也就是说满足传递性，并且此时的  都是核心对象。只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性，这个可以由密度直达的不对称性得出。

（讲的很绕，简而言之，上图的右侧有五个红点，都是核心对象，核心对象和核心对象之间密度直达，因为两两之间都密度直达，那么最上面那个核心对象和最下面那个核心对象密度可达，说明传递性）

密度相连：

对于  和  ，存在核心对象  ，对于  和  均有  密度可达，则称   和  密度直连，密度相连关系是满足对称性的。

（其实很好理解，还是上图右侧的第一个红点，这个红点和它上方的黑点密度可达，并且和第二个红点也密度可达，那么，第一个红点上方的黑点与第二个红点是密度相连的，以此类推）

 

DBSCAN密度聚类思想

DBSCAN的聚类定义很简单：由密度可达关系导出的最大密度相连的样本集合，即为我们最终聚类的一个类别，或者说一个簇。

　　　　这个DBSCAN的簇里面可以有一个或者多个核心对象。如果只有一个核心对象，则簇里其他的非核心对象样本都在这个核心对象的ϵ-邻域里；如果有多个核心对象，则簇里的任意一个核心对象的ϵ-邻域中一定有一个其他的核心对象，否则这两个核心对象无法密度可达。这些核心对象的ϵ-邻域里所有的样本的集合组成的一个DBSCAN聚类簇。

　　　　那么怎么才能找到这样的簇样本集合呢？DBSCAN使用的方法很简单，它任意选择一个没有类别的核心对象作为种子，然后找到所有这个核心对象能够密度可达的样本集合，即为一个聚类簇。接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合，这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止。

　　　　基本上这就是DBSCAN算法的主要内容了，是不是很简单？但是我们还是有三个问题没有考虑。

　　　　第一个是一些异常样本点或者说少量游离于簇外的样本点，这些点不在任何一个核心对象在周围，在DBSCAN中，我们一般将这些样本点标记为噪音点。

　　　　第二个是距离的度量问题，即如何计算某样本和核心对象样本的距离。在DBSCAN中，一般采用最近邻思想，采用某一种距离度量来衡量样本距离，比如欧式距离。这和KNN分类算法的最近邻思想完全相同。对应少量的样本，寻找最近邻可以直接去计算所有样本的距离，如果样本量较大，则一般采用KD树或者球树来快速的搜索最近邻。

　　　　第三种问题比较特殊，某些样本可能到两个核心对象的距离都小于ϵ，但是这两个核心对象由于不是密度直达，又不属于同一个聚类簇，那么如果界定这个样本的类别呢？一般来说，此时DBSCAN采用先来后到，先进行聚类的类别簇会标记这个样本为它的类别。也就是说DBSCAN的算法不是完全稳定的算法。

DBSCAN的主要优点有：

　　　　1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

　　　　2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

　　　　3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

　　　　1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

　　　　2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

　　　　3） 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

 

DBSCAN伪代码

看了很多理论的东西该上实际点的东西了：

//觉得上面已经把定义介绍的非常清晰了，来先更具想法肝一个伪代码
//参考《数据挖掘概念与技术》

初始化参数
坐标样本集： D (x1, x2, ...... , xm)        （这里是在网上找的一个很多点的txt文本）
邻域参数：  ϵ (相当于超球体的半径)    MinPts  (最小个数)
距离度量方式： 欧式距离

初始化所有的点为unvisited
while 所有unvisited样本:
    有unvisited样本p;
    将p记为visited;
    # 其实这里只是在计算核心对象，如果计算完不满足核心对象的话直接为噪声，不考虑非核心对象，因为簇由核心对象决定
    if p的ϵ-邻域里有MinPts个其他样本:
        创建新簇C，将p添加到C;
        设置N为p的ϵ-邻域里的所有对象的集合
        # 遍历N中的所有的点
        for N中每个点 p':
            if p'是unvisited:
                将p'记为visited;
                if p'的ϵ-邻域里有MinPts个其他样本:
                    将这些样本添加到N;
                if p'不是任何簇的成员:
                    将p'添加到C
    else 标记p为噪声;


(个人疑点：若是被记为噪声的点被某个核心样本的ϵ-邻域包含即代表非核心样本被划分为噪声了，但《数据挖掘概念与技术》确实如此描述)

 

DBSCAN基于python的实现

上面给出伪代码，接下来要用python实现一遍了：

基于python的实现方式和上面书中的伪代码稍有出入，给出我自己的思路的伪代码：

初始化参数
坐标样本集： D (x1, x2, ...... , xm)        （这里是在网上找的一个很多点的txt文本）
邻域参数：  ϵ (相当于超球体的半径)    MinPts  (最小个数)
距离度量方式： 欧式距离

初始化所有的点为unvisited
while 所有unvisited样本:
    有unvisited样本p;
    将p记为visited;
    # 其实这里只是在计算核心对象，如果计算完不满足核心对象的话直接为噪声，不考虑非核心对象，因为簇由核心对象决定
    if p的ϵ-邻域里有MinPts个其他样本:
        创建新簇C，将p添加到C;
        设置N为p的ϵ-邻域里的所有对象的集合
        # 遍历N中的所有的点
        for N中每个点 p':
            if p'是unvisited:
                将p'记为visited;
                if p'的ϵ-邻域里有MinPts个其他样本:
                    将这些样本添加到N;
                if p'不是任何簇的成员:
                    将p'添加到C
            # 这一步是自己新添的
            if p'是噪声:
                抹去噪声标记并添加到C
    else 标记p为噪声;

# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import math

# 未访问
UNVISITED = -2
# 噪声
NOISE = -1


def dist(a, b):
    """
    输入：向量A, 向量B
    输出：两个向量的欧式距离
    公式略
    """
    return math.sqrt(np.power(a - b, 2).sum())


def whether_neighbor(a, b, radius):
    """
    输入：向量A, 向量B
    输出：是否在领域内
    """
    return dist(a, b) < radius


def whether_kernel_object(dataSet, selectId, radius):
    """
    输入：数据集, 查询是否是核心对象的点id, 半径大小ϵ
    输出：[ 在领域范围内的点的id ]
    """
    # 计算在领域范围内有多少点
    return [i for i in range(dataSet.shape[0]) if whether_neighbor(a=dataSet[selectId], b=dataSet[i], radius=radius)]


def visualization(dataSet, resultSet, clusterNumber):
    """
    实现可视化
    输入：数据集, 结果集, 簇个数
    """
    # 转一下
    matResult = np.mat(resultSet).transpose()
    dataSet = dataSet.transpose()
    # 图
    figure = plt.figure()
    # 取红橙黄绿蓝几种颜色
    colors = ['green', 'blue', 'orange', 'yellow', 'red']
    # 一行一列第一个
    ax = figure.add_subplot(111)
    # 遍历每一个簇
    for i in range(clusterNumber + 1):
        # 选一种颜色，若是簇的数目超过颜色数的话从头选
        color = colors[i % len(colors)]
        sub = dataSet[:, np.nonzero(matResult[:, 0].A == i)]
        # 画点 前两个参数为坐标
        ax.scatter(sub[0, :].flatten().A[0], sub[1, :].flatten().A[0], c=color, s=40)
    plt.show()


if __name__ == '__main__':
    # 初始化参数(懒得写在文件开头了)
    # 半径
    radius = 2
    # 最小点数
    minPts = 15
    with open("points.txt") as file:
        # 分行, 逗号分隔,转成list
        dataSet = [list(map(float, line.strip().split(","))) for line in file.readlines()]
    dataSet = np.mat(dataSet)
    # 点的数目
    pointNumber = dataSet.shape[0]
    # 和伪代码一致先将所有的点标为未访问，flagClusterList最终是存放每个点的判定结果，例如簇几、噪声
    flagClusterList = [UNVISITED] * pointNumber
    # 簇的数目，也算作下标，从簇1开始
    # (当前的簇)
    clusterNumber = 1
    # 开始遍历
    for selectPoint in range(pointNumber):
        # 如果点没有被分类
        if flagClusterList[selectPoint] == UNVISITED:
            # 找出邻域里的点
            neighbors = whether_kernel_object(dataSet=dataSet, selectId=selectPoint, radius=radius)
            # 不满足最小点
            if len(neighbors) < minPts:
                flagClusterList[selectPoint] = NOISE
            else:
                # 划分到当前簇
                flagClusterList[selectPoint] = clusterNumber
                # 先将邻域里的其他点装到簇里（和伪代码一致）
                for neighborsId in neighbors:
                    # 未访问过或是噪声(若是其他簇的话按照先来后到的顺序)
                    if flagClusterList[neighborsId] == UNVISITED or flagClusterList[neighborsId] == NOISE:
                        flagClusterList[neighborsId] = clusterNumber
                # 扩张
                while len(neighbors) > 0:
                    # 掏出第一个点
                    currentPoint = neighbors[0]
                    # 查询当前点邻域中的点
                    queryNeighbors = whether_kernel_object(dataSet=dataSet, selectId=currentPoint , radius=radius)
                    # 如果大于等于最小点
                    if len(queryNeighbors) >= minPts:
                        for i in range(len(queryNeighbors)):
                            # 将新的邻域点取出存到N中
                            resultPoint = queryNeighbors[i]
                            if flagClusterList[resultPoint] == UNVISITED:
                                # 如果未访问的话继续往下找，继续扩展
                                neighbors.append(resultPoint)
                                flagClusterList[resultPoint] = clusterNumber
                            # 和上面思想一致
                            elif flagClusterList[resultPoint] == NOISE:
                                flagClusterList[resultPoint] = clusterNumber
                    # 因为N中第一个拿过了，需要刷新
                    neighbors = neighbors[1:]
                # 该簇结束，创建一个新簇
                clusterNumber += 1

    print("簇的个数：" + str(clusterNumber - 1))
    # 遍历结束
    # 绘图实现可视化
    visualization(dataSet, flagClusterList, clusterNumber - 1)

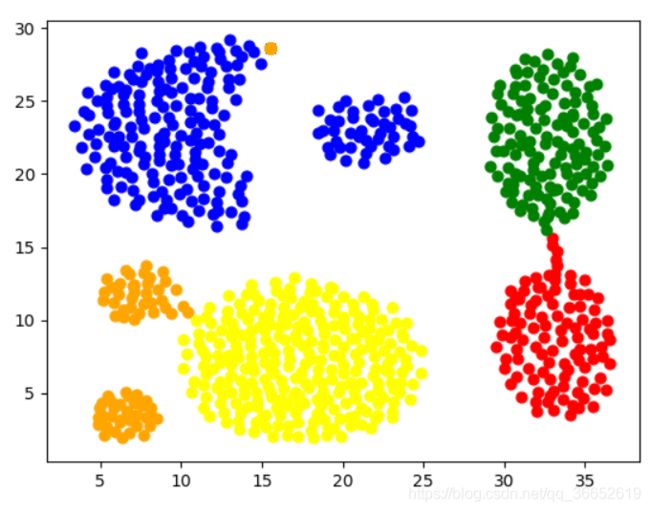
结果：

point.txt是在网上找的一个资源这里也贴出来：

15.55,28.65
14.9,27.55
14.45,28.35
14.15,28.8
13.75,28.05
13.35,28.45
13,29.15
13.45,27.5
13.6,26.5
12.8,27.35
12.4,27.85
12.3,28.4
12.2,28.65
13.4,25.1
12.95,25.95
12.9,26.5
11.85,27
11.35,28
11.15,28.7
11.25,27.4
10.75,27.7
10.5,28.35
9.65,28.45
10.25,27.25
10.75,26.55
11.7,26.35
11.6,25.9
11.9,25.05
12.6,24.05
11.9,24.5
11.1,25.2
10.55,25.15
10.05,25.95
9.35,26.6
9.3,27.25
9.2,27.8
7.5,28.25
8.55,27.45
8.5,27.05
8.05,27.2
7.85,26.8
7.3,27.4
6.8,26.85
7,26.5
7.55,26.3
8.55,26.3
9,25.85
8.6,25.65
9.4,25.55
8.45,25.05
8.85,24.6
9.65,24.7
10.55,24.35
11.05,23.9
10.55,23.55
9.45,23.35
9.2,23.9
8.35,23.9
7.35,24.75
7.4,25.45
6.6,25.75
6.1,26
5.8,26.95
5.65,25.8
5.3,26.1
6.4,25.4
5.4,25.25
5.35,24.7
4.8,25.05
4.2,25.55
6.4,24.8
6.55,24.3
7.4,24.25
5.45,24.2
4.3,24
4,24.25
3.35,23.3
4.85,23.05
4.3,22.75
5.85,23.4
5.9,23.55
7.55,23.7
6.85,23.25
7.65,23.1
6.95,22.55
6.1,22.6
5.5,22.6
4.7,22.1
3.8,21.85
4.65,21.2
4.15,20.35
5.3,20.4
5.6,20.75
5.8,21.95
6.4,21.95
6.55,21.15
7.45,21.95
7.4,21.55
7.75,21.2
7.65,20.65
6.95,19.8
6.6,20.1
6.05,20.2
5.4,19.65
5.35,19.05
5.8,18.25
6.3,19.1
7,18.9
7.15,17.9
7.35,18.2
8.2,20.05
8.3,19.45
8.3,18.5
8.75,18.8
9.05,18.2
9.35,17.7
8.9,17.65
8.45,17.2
10.05,17.2
10.4,16.75
8.6,20.9
8.65,21.3
8.65,21.9
8.65,22.5
8.95,22.8
9.95,22.65
8.95,22.2
9.65,21.9
10.55,22.3
10.9,22.85
11.35,23.45
12.05,23.4
12.3,22.75
11.7,22.15
11.15,22.05
10.85,21.5
10.85,21.05
9.6,21.3
9.85,20.7
9.35,20.6
9.25,19.65
9.95,19.8
10.7,20.35
11.3,20.7
12.35,21.6
13.1,21.3
12.85,20.75
12,20
11,19.85
10.35,19
9.9,18.65
10.6,18.15
11.4,18.3
11.4,19.25
12.35,18.8
12.8,19.75
12.15,18.1
11.05,17.5
11.95,17.25
12.25,17.5
13.05,17.4
13.75,18.15
13.5,18.65
13.65,19.25
14,19.9
15.2,18.2
15.5,17.15
13.9,17.1
13.75,16.6
12.15,16.4
7.8,13.7
8.85,13.35
9,12.7
9.7,12.1
8.05,12.9
7.7,13.25
6.8,13.2
6.6,13.45
6.2,12.55
5.4,12.85
5.7,12.25
5.2,11.9
5.15,11.35
5.85,11.2
6.1,11.75
7,12.35
7.05,12.45
7.9,12.5
8.55,12.1
7.85,11.85
7.1,11.95
6.9,11.5
6.85,10.9
6.4,10.7
5.9,10.3
6.4,10.25
7.05,10.05
7.35,10.5
7.65,11.1
8.1,11.2
8.8,11.4
8.3,10.55
9,10.9
9.35,10.5
10.15,11
10.4,10.55
10.9,10
11.55,10.2
11.75,10.85
10.1,8.65
11.05,9.1
11.85,9.8
12.85,10.65
12.9,11.7
13.6,11.1
14.05,11.75
14.5,11.8
14.3,12.45
17,12.9
15.8,12.6
15.85,12
16.7,12.2
16.25,11.7
15.55,11.15
14.8,11.35
14.45,10.75
13.75,10.45
12.8,10.1
13.15,9.8
12.45,9.3
11.8,8.95
11.1,8.45
10.35,7.7
10.1,6.75
11.3,7.95
12.35,8.45
13.1,8.95
13.2,9.35
14.1,10.05
11.5,7.5
11.35,6.9
11.95,6.75
12.4,7.1
12.25,7.6
12.95,7.6
13.45,7.95
13.35,8.25
13.75,9
14.3,9.3
14.85,9.55
15.1,10.25
15.45,10.55
16.35,10.85
16.75,11.5
16.25,10.2
15.4,10.1
15.45,9.7
15.15,9.3
15.25,8.65
15.55,8.2
14.25,8.7
14.25,8.25
15.05,7.8
14.3,7.5
13.55,7.45
14.3,6.95
13.95,6.7
13.05,6.95
13.05,6.2
11.55,6.3
10.8,5.85
10.6,5.05
11.35,5.55
12.15,5.4
12.4,5.8
12.8,5.7
13.65,5.9
13.9,5.3
13.1,5.1
12.55,4.9
11.5,4.75
11.35,4.05
12.4,4.35
11.75,3.45
12.65,3.7
13.4,4.35
13.9,4.95
12.75,3
13.55,3.15
13.7,3.65
14.1,4.1
14.65,5.05
14.35,5.75
14.5,6.55
15.15,7.1
13.6,2.55
14.45,2.4
14.6,3.05
15,3.4
15.25,3.5
14.7,4.1
14.7,4.5
15.25,2.7
15.65,2.05
15.95,2.8
16.1,3.55
15.9,4
15.6,4.75
15.55,5.05
15.35,5.5
15.15,5.95
15.5,6.75
15.7,6.35
16.2,5.9
16.35,5.35
16.2,4.55
16.55,4.2
16.95,4.75
17.05,5.1
17.3,4.8
17.3,4.15
17.6,4.3
17.05,3.7
17.25,3.05
16.65,2.8
16.55,2.15
17.2,2.05
18.15,1.95
18.05,2.45
18.15,3.05
18.6,3.45
18.4,3.6
18.85,3.2
19.1,2.65
19.45,2.65
19,2.1
19.9,2.05
20.45,2.8
19.8,3.25
19.45,3.9
18.65,4.2
18.4,4.6
18.65,4.75
18.75,5.15
19.1,4.55
17.9,5.4
17.65,5.7
17.05,6.05
17.4,6.5
16.6,6.85
15.7,7.15
15.75,7.75
16.6,7.95
20.4,3.4
20.7,3.45
21.15,2.85
21.75,2.65
22,3.25
22.2,3.5
21.45,3.75
21.1,4.05
20.15,4.3
20.8,4.7
20.7,5.15
19.75,5.05
19.85,5.5
20.4,5.65
20.55,5.75
18.7,5.75
19.25,5.95
18.4,6
18.45,6.6
17.65,7.05
16.7,7.4
18.65,7.3
18.05,7.35
17.85,7.75
17.5,8.25
17.15,8.6
17.05,9
16.4,8.7
16.05,8.95
16.05,9.6
16.5,9.75
17.25,9.6
17.6,9.9
17.8,9.3
18,8.55
18.8,8.1
18.8,8.35
19.4,7.6
19.25,6.6
20.05,6.95
19.8,7.5
20.05,6.35
21.15,5.7
21.65,4.85
22.15,4.35
23.05,3.35
23.05,3.8
23.15,4.4
22.5,4.75
22.15,5.2
24.15,4.55
23.5,5.05
23.1,5.3
23,5.75
22.2,5.75
21.85,6.2
20.75,6.55
21,7.15
20.75,7.65
20,8.2
19.5,8.65
18.85,9.05
18.75,9.55
18.6,10
16.95,10.35
17.35,10.85
18,10.65
18.5,10.55
18.1,11.1
17.55,11.3
17.95,11.9
18.3,12
18,12.5
19,11.65
19.5,11.05
19.45,10.55
19.4,9.65
20.1,9.4
20.05,9.95
20.05,10.2
19.35,12.2
19.2,12.25
20.05,11.6
20.6,11.15
20.7,10.65
21.3,11.65
21.8,11.15
21.85,10.7
21.65,10.05
20.95,10.2
20.9,9.7
21.65,9.45
21.2,9.25
20.75,8.75
20.55,8.75
21.1,8
21.65,8.65
21.75,8.2
21.95,7.55
22,6.75
22.8,6.45
22.65,6.65
22.75,7.05
23,7.35
22.55,7.9
22.2,8.7
22.9,8.45
22.35,9.2
22.75,9.35
22.4,10.05
23.05,10.9
23.3,9.85
23.95,9.8
23.65,9.1
23.7,8.85
24.25,8.25
24.85,7.95
23.5,7.85
23.85,7.35
23.95,6.9
23.65,6.5
23.6,5.7
24.3,5.65
24.8,6.4
34.05,3.5
33.05,3.85
32,3.8
31.9,4.4
31.05,4.75
30.4,5.65
30.75,6.1
30,6.7
30.1,7.4
29.5,8.15
30.75,8
30.85,7.35
31.5,6.75
31.75,5.95
32.35,6.45
32.8,6
32.05,5.1
32.8,4.8
32.65,4.4
33.65,4.6
33.05,5.15
33.6,5.45
34.5,5.05
34.9,4.65
35.45,4.1
34.6,4.05
34.2,4.2
36.3,5.2
35.55,5.35
35.95,6.05
34.8,5.85
33.7,6.15
33.95,6.6
33.7,7.05
32.75,7.1
32.3,7.65
33,7.9
31.95,8.15
31.15,8.65
30.35,8.85
29.85,9
30.7,9.15
29.7,9.9
30.45,9.95
30.95,9.85
31.8,9.45
32.45,8.8
33.55,8.6
34.35,7.7
34.7,8
34.6,7.25
35,6.8
35.5,7.35
36.1,7.5
36.55,7
36,8.2
35.35,8.05
36.55,8.65
36.4,9.1
35.5,9.1
34.55,8.85
35.25,9.4
34.4,9.5
33.5,9.3
33.85,9.8
32.5,9.65
32.3,10.25
33.3,10.3
31.6,10.5
30.6,10.5
30.4,11.1
30.9,11.45
30.7,11.65
30.4,12.05
31.2,12
31.95,11.35
31.65,11.05
32.95,11.15
32.65,11.7
32.25,12.25
32.05,12.25
31.3,12.7
31.95,12.95
32.75,13.1
33.15,13.2
33.1,12.75
33.15,12.1
34.3,11.75
34,10.85
34.65,11
34.8,10.1
35.65,9.85
36.35,10
35.55,10.75
35.8,11.55
35.2,11.75
34.7,11.75
34.95,12.75
34.05,12.55
34.05,13.05
33.25,13.7
33.2,14.15
33.25,14.7
33,15.15
32.95,15.65
32.6,16.15
32.45,16.75
32.65,17.05
32.75,17.3
31.75,17.2
31.7,17.65
31,17.5
31.15,17.9
30.45,18.05
30.05,18.8
30.55,18.8
30.5,19.3
30.25,19.4
29.6,19.85
29.15,20.55
30.25,20.45
30.7,20.05
31,19.9
31.55,19.65
31.5,18.55
32.05,18.6
31.95,19.1
32.6,18.35
32.85,17.95
33.45,17.45
33.7,17
34.25,17.35
34.3,18.05
33.85,18.4
33.05,18.85
33.25,18.95
32.8,19.15
32.3,19.85
32.8,20
31.75,20.25
31.75,20.75
32.1,21.15
31.55,21.6
30.65,21.3
29.95,21.6
29.5,21.6
30.35,22.05
31.05,22
31.55,22.2
30.95,22.65
30.3,23.1
29.6,23.15
29.35,22.55
29.2,23.85
30.75,24
30.95,24.15
31.45,23.7
31.95,23.15
32.55,22.05
32.6,22.55
33.25,22.25
33.65,21.9
33.5,21.3
33.1,20.75
33.8,20.4
33.85,20
34.15,19.3
34.85,18.85
35.3,18.55
35.4,19.35
34.55,19.75
35.05,20
35.95,19.85
36.35,20.6
35.5,20.55
34.45,20.65
34.4,21.25
35,21.05
35.75,21.3
35.05,21.5
34.6,22.05
34.2,21.75
36.25,21.95
35.7,22.3
35.5,22.9
35.85,23.25
36.3,23.8
35.45,24.1
34.9,23.5
34.2,22.9
33.85,23.3
33.25,23.35
32.45,23.7
33.6,23.9
34.25,23.95
34.25,24.1
35.4,24.7
35.15,25.3
34.4,24.9
33.7,24.85
32.25,24.45
32.5,24.7
31.45,24.45
31.55,25.2
31.05,25
30.25,24.3
29.8,24.8
29.6,25.5
29.7,26.05
30.5,25.5
30.65,26
31.25,26.05
31.45,26.95
30.75,26.9
30.65,27.15
31.25,27.85
31.85,27.75
32.7,28.2
33.25,27.55
32.4,27.1
32.15,26.65
32.35,25.95
32.95,25.5
33.85,26.05
33.05,26.5
33.65,27
34.1,27.35
34.2,27.95
34.65,26.85
35.25,26
35.7,26.15
34.4,25.6
21.3,20.8
20.15,20.9
19.2,21.35
19.1,21.85
18.45,22.8
18.75,22.95
19.4,23
19.55,22.25
19.8,21.85
20.5,21.85
21.45,21.45
21.7,21.9
21.4,22.3
21,22.6
21.15,22.95
20.5,22.85
19.75,23.65
19.2,23.7
18.45,24.35
20.65,23.85
20.65,24.3
19.7,24.6
20.15,25.05
22.15,25.1
21.6,24.65
21.7,23.8
21.9,23.65
22.55,23.5
22.55,24.3
23.3,24.45
24.25,24.35
23.8,25.25
23.4,23.8
22.9,23.2
22.3,22.8
22.2,22.4
23.1,21.7
22.85,21.9
22.65,21.1
23.15,22.6
24.1,21.9
24.7,22.2
24.3,22.6
24.15,23.3
23.9,23.45
5.2,2.15
6.35,1.95
6.75,2.3
5.9,2.4
5.4,2.7
4.85,2.9
4.85,3.35
5.15,3.45
5.7,3.45
6.2,3
6.2,3.2
7.65,2.15
7.2,2.75
6.75,3.2
6.75,3.55
6.65,3.8
5.8,4
4.95,4.05
5.1,4.35
5.7,4.45
5.45,4.85
6.7,4.8
6.55,5.05
7.2,4.9
6.2,4.25
7.1,4.3
7.85,4.5
7.6,4.15
7.25,3.55
7.8,3.35
8.05,2.75
8.5,3.25
8.1,3.55
8.15,4

 

该方向并非主方向，业余玩耍，不喜勿怼哈

参考博客：

https://www.cnblogs.com/pinard/p/6208966.html