两种经典的单源最短路径算法图解与java实现（贪心Dijkstra和A*）

单源最短路径典型的启发式搜索有两种，分别是贪婪最佳优先搜索（Greedy best-first search）和A*寻路搜索。这篇文章以最短路径问题为例来展开讨论两种搜索方法的思路。

First Step:确定路径的存储结构

可求最短路径的结构往往是有向带权图，用代码表示就是

public class Graph {
      // 有向有权图的邻接表表示
  private LinkedList<Edge> adj[]; // 邻接表
  private int v; // 顶点个数
  public Graph(int v) {
     
    this.v = v;
    this.adj = new LinkedList[v];
    for (int i = 0; i < v; ++i) {
     
      this.adj[i] = new LinkedList<>();
    }
  }
  public void addEdge(int s, int t, int w) {
      // 添加一条边
    this.adj[s].add(new Edge(s, t, w));
  }
  private class Edge {
     
    public int sid; // 边的起始顶点编号
    public int tid; // 边的终止顶点编号
    public int w; // 权重
    public Edge(int sid, int tid, int w) {
     
      this.sid = sid;  this.tid = tid;  this.w = w;
    }
  }
  //这个类是为了dijkstra实现用的
  private class Vertex {
     
    public int id; // 顶点编号ID
    public int dist; // 从起始顶点到这个顶点的距离
    public Vertex(int id, int dist) {
     
      this.id = id;
      this.dist = dist;
    }
  }
}

Second Step:不同寻路算法实现

1.贪婪最佳优先搜索——Dijkstra算法

  用贪心思路，每一步都选最优。不足之处有：（1）没办法保证全局最优，甚至可能选入死循环路径。（2）时间复杂度和空间复杂度最坏情况都可达到O(b^m)，b是所有结点总数，m是搜索空间的最大深度

Dijkstra算法是贪心/BFS的升级版。当一个图中的每条边都加上权值后，BFS就没办法求一个点到另一个点的最短路径了。这时候，需要用到Dijkstra算法。从最基本原理上讲，把BFS改成Dijkstra算法，只需要把“队列”改成“优先队列”就可以了。
四个核心参数：
vertexs[i]：V0到Vi的最短路径长度（或权重）。
predecessor[i]：存当前最短路径上的倒数第二个结点。
PriorityQueue ：每一位存Vi以及vertexs[i]，会自动根据vertex[i]的值排序，小顶堆。
inqueue[i]：bool变量，Vi计入最短路径则为1，不计入为0；

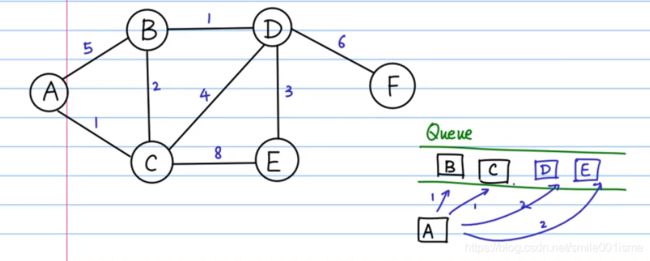
图片来源：BFS算法讲解

// 因为Java提供的优先级队列，没有暴露更新数据的接口，所以我们需要重新实现一个
private class PriorityQueue {
      // 根据vertex.dist构建小顶堆
  private Vertex[] nodes;
  private int count;
  public PriorityQueue(int v) {
     
    this.nodes = new Vertex[v+1];
    this.count = v;
  }
}
public void dijkstra(int s, int t) {
      // 从顶点s到顶点t的最短路径
  int[] predecessor = new int[this.v]; // 用来还原最短路径
  Vertex[] vertexes = new Vertex[this.v];
  for (int i = 0; i < this.v; ++i) {
     
    vertexes[i] = new Vertex(i, Integer.MAX_VALUE);
  }
  PriorityQueue queue = new PriorityQueue(this.v);// 小顶堆
  boolean[] inqueue = new boolean[this.v]; // 标记是否进入过队列
  vertexes[s].dist = 0;
  queue.add(vertexes[s]);
  inqueue[s] = true;
  while (!queue.isEmpty()) {
     
    Vertex minVertex= queue.poll(); // 取堆顶元素并删除
    if (minVertex.id == t) break; // 最短路径产生了
    for (int i = 0; i < adj[minVertex.id].size(); ++i) {
     
      Edge e = adj[minVertex.id].get(i); // 取出一条minVetex相连的边
      Vertex nextVertex = vertexes[e.tid]; // minVertex-->nextVertex
      if (minVertex.dist + e.w < nextVertex.dist) {
      // 更新next的dist
        nextVertex.dist = minVertex.dist + e.w;
        predecessor[nextVertex.id] = minVertex.id;
        if (inqueue[nextVertex.id] == true) {
     
          queue.update(nextVertex); // 更新队列中的dist值
        } else {
     
          queue.add(nextVertex);
          inqueue[nextVertex.id] = true;
        }
      }
    }
  }
  // 输出最短路径
  System.out.print(s);
  print(s, t, predecessor);
}
private void print(int s, int t, int[] predecessor) {
     
  if (s == t) return;
  print(s, predecessor[t], predecessor);
  System.out.print("->" + t);
}

2.A*算法

Dijkstra算法是用一个优先队列来记录遍历的顶点与相应路径长度，如果顶点到起点的路径约短，就越先从队列中取出来做扩展，虽然最后在整个图里找到最有路径，但是开头难免曲折。（最优路径可能开始的边权重很大）
快速寻路的A算法应运而生，不足是它只能找到次优解，不能保证最优。
A算法评估函数公式f(i) = g(i) + h(i) ; 而Dijkstra算法是f(i) = g(i) ;
其中g(i)是从起始到当前结点n的最小代价值 ,h(i)是从当前到目标结点路径的最小代价值，f（i）是经过结点i，具有最小代价值的路径。
其中h(i)一般可以通过
A* 算法的代码实现的主要逻辑是下面这段代码。它跟 Dijkstra 算法的代码实现，主要有 3 点区别：
优先级队列构建的方式不同。A* 算法是根据 f 值（也就是刚刚讲到的 f(i)=g(i)+h(i)）来构建优先级队列，而 Dijkstra 算法是根据 dist 值（也就是刚刚讲到的 g(i)）来构建优先级队列；

public void astar(int s, int t) {
      // 从顶点s到顶点t的路径
  int[] predecessor = new int[this.v]; // 用来还原路径
  // 按照vertex的f值构建的小顶堆，而不是按照dist
  PriorityQueue queue = new PriorityQueue(this.v);
  boolean[] inqueue = new boolean[this.v]; // 标记是否进入过队列
  vertexes[s].dist = 0;
  vertexes[s].f = 0;
  queue.add(vertexes[s]);
  inqueue[s] = true;
  while (!queue.isEmpty()) {
     
    Vertex minVertex = queue.poll(); // 取堆顶元素并删除
    for (int i = 0; i < adj[minVertex.id].size(); ++i) {
     
      Edge e = adj[minVertex.id].get(i); // 取出一条minVetex相连的边
      Vertex nextVertex = vertexes[e.tid]; // minVertex-->nextVertex
      if (minVertex.dist + e.w < nextVertex.dist) {
      // 更新next的dist,f
        nextVertex.dist = minVertex.dist + e.w;
        nextVertex.f 
           = nextVertex.dist+hManhattan(nextVertex, vertexes[t]);
        predecessor[nextVertex.id] = minVertex.id;
        if (inqueue[nextVertex.id] == true) {
     
          queue.update(nextVertex);
        } else {
     
          queue.add(nextVertex);
          inqueue[nextVertex.id] = true;
        }
      }
      if (nextVertex.id == t) {
      // 只要到达t就可以结束while了
        queue.clear(); // 清空queue，才能推出while循环
        break; 
      }
    }
  }
  // 输出路径
  System.out.print(s);
  print(s, t, predecessor); // print函数请参看Dijkstra算法的实现
}

A* 算法在更新顶点 dist 值的时候，会同步更新 f 值；
循环结束的条件也不一样。Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。
A* 算法之所以不能像 Dijkstra 算法那样，找到最短路径，主要原因是两者的 while 循环结束条件不一样。刚刚我们讲过，Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。对于 Dijkstra 算法来说，当终点出队列的时候，终点的 dist 值是优先级队列中所有顶点的最小值，即便再运行下去，终点的 dist 值也不会再被更新了。对于 A* 算法来说，一旦遍历到终点，我们就结束 while 循环，这个时候，终点的 dist 值未必是最小值。