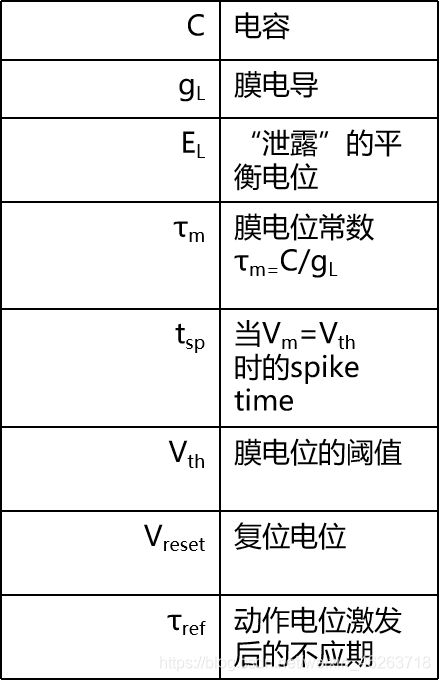
The Leaky Integrate-and-Fire (LIF) Neuron Mode-LIF神经元模型

The Leaky Integrate-and-Fire (LIF) Neuron Mode

基础知识

1.在产生动作电位之前，进入突触接触部位的电流必须沿树突向下扩散并穿过神经元胞体，并导致尖峰起始区的膜去极化超过阈值，导致兴奋性突触后电位的整合。换句话说动作电位建模有三个阶段分别是：突触；树突；神经元胞体

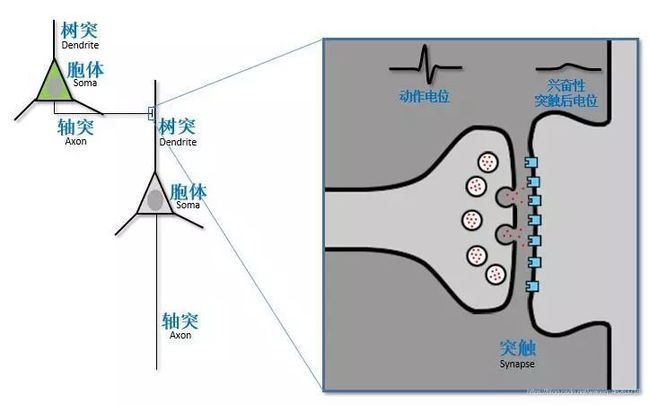
2.泄露电流：可以想象突触中的正电荷流入就像打开水一样，水会从漏水的花园软管（树突）中流下来。 水可以采取两种途径：沿着软管内部或通过泄漏。 同样，突触电流可以通过两条路径：沿着树突内部或穿过树突膜。 当电流沿着树突向下，离突触更远， 由于离子电流通过膜通道的泄漏，EPSP（兴奋性突触后电位）振幅将减小。

膜作为电路的生物物理学

想象一个离子电流在树突内流动，如基础知识中提到的一样，电流的流动存在两种途径：沿着树突内部或穿过树突膜；因此换一种说法就送当离子电流撞击树突的细胞膜时存在两种后果：造成膜电位的改变或泄露出膜
大多数电流将采取最小电阻的路径；因此，随着膜电阻的增加，更多的去极化电流将在树突内部流动而不是“泄漏”出膜。 随着内阻的增加，更多的电流会泄露出膜。
以下为膜电路的具体讲解：

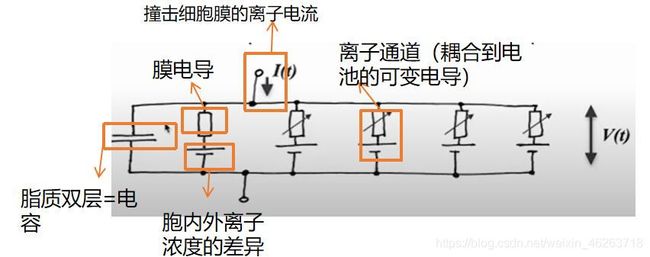
树突膜的脂质双层在电路中表示为电容器，因为电荷可以积累在膜的两侧，这一性质也叫做膜的电容；由于树突内电流对于路径的选择会取决于膜电阻，因此在电路中用一个膜电导来表示（g=1/R）；由于胞内外存在离子浓度的差异，因此代表脂质双层的电容器连接了一个电源，通过极板内外电荷的差异来模拟离子浓度的差异；由于动作电位的发生需要钠钾离子通道的开放，而这些离子通道的开放和关闭都是不定的，因此用一个耦合到电池的可变电导来指代这些离子通道。

膜电位的一阶微分方程

在LIF模型中忽略了那些不直接参与动作电位的离子通道（可能起到很重要的调控作用）

经过一系列简单的数学变换，最终将膜电位的一阶微分方程转变为上图形式

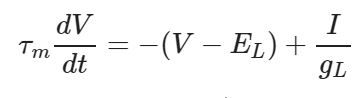
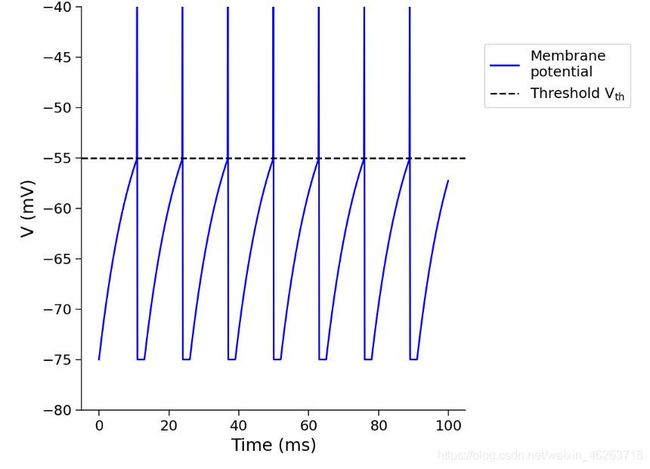
随后对动作电位的激发过程作出定义：达到阈值-激发动作电位-复位到平衡电位-绝对不应期
当膜电位达到或超过阈值，此时的膜电位会被重置为复位电位并在绝对不应期保持，随后再次开始下一个循环

下图为涉及的所有参数

整个过程的代码实现

def run_LIF(pars, Iinj, stop=False):
  """
  Simulate the LIF dynamics with external input current
  Args:
    pars       : parameter dictionary
    Iinj       : input current [pA]. The injected current here can be a value
                 or an array
    stop       : boolean. If True, use a current pulse
  Returns:
    rec_v      : membrane potential
    rec_sp     : spike times
  """
  # Set parameters
  V_th, V_reset = pars['V_th'], pars['V_reset']
  tau_m, g_L = pars['tau_m'], pars['g_L']
  V_init, E_L = pars['V_init'], pars['E_L']
  dt, range_t = pars['dt'], pars['range_t']
  Lt = range_t.size
  tref = pars['tref']

  # Initialize voltage and current
  v = np.zeros(Lt)
  v[0] = V_init
  Iinj = Iinj * np.ones(Lt)
  if stop:  # set end of current to 0 if current pulse
    Iinj[:int(len(Iinj) / 2) - 1000] = 0
    Iinj[int(len(Iinj) / 2) + 1000:] = 0
  tr = 0.  # the count for refractory duration

  # Simulate the LIF dynamics
  rec_spikes = []  # record spike times
  for it in range(Lt - 1):
    if tr > 0:  # check for refractoriness
      v[it] = V_reset
      tr = tr - 1
    elif v[it] >= V_th:  # reset voltage and record spike event
      rec_spikes.append(it)
      v[it] = V_reset
      tr = tref / dt

    # calculate the increment of the membrane potential
    dv = (-(v[it] - E_L) + Iinj[it] / g_L) * (dt / tau_m)

    # update the membrane potential
    v[it + 1] = v[it] + dv

  rec_spikes = np.array(rec_spikes) * dt

  return v, rec_spikes


pars = default_pars(T=500)
v, sp = run_LIF(pars, Iinj=100, stop=True)

引用

恒定电流

高斯白噪声（GWN）电流

在存在噪声的情况下，spike可以由噪声带来的波动所驱使，随机波动在一定可能下恰好足以触发响应，使得神经元放电，而这种波动驱使倾向于在膜电位没有达到阈值时出现，在达到阈值后便转为平均驱动

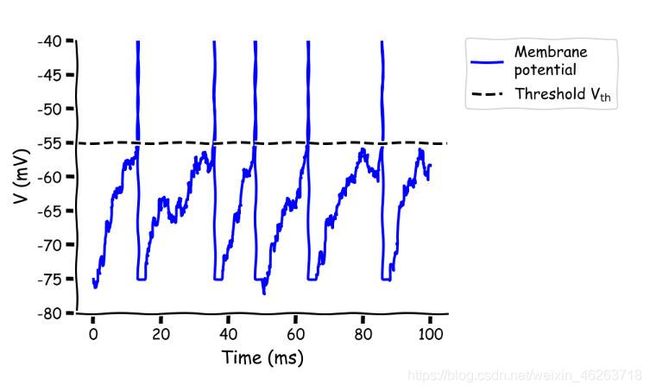
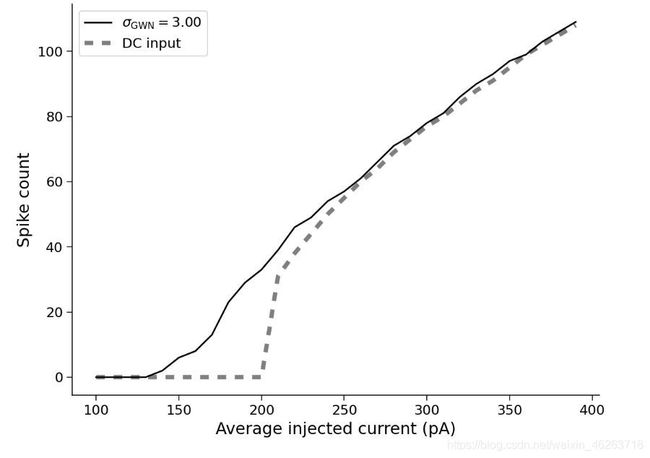
LIF模型不足

1.在之前提到过，LIF模型忽略了除钠钾通道外其他离子通道的开放对于动作电位产生的影响
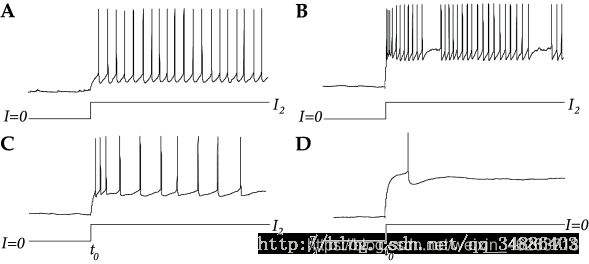
2.当输入电流时，真实神经元有一个适应的过程，即从当输入一个恒定的电流I（从0到K整个过程），根据LIF模型，我们可以推断发放率应该是恒定的，这是因为reset的存在。但在真实神经元并非这样工作，需要经过一个过程才能输出稳定的发放率。快速脉冲神经元（fast-spiking），其本身就没有适应性所以可以很好的对应LIF模型；除了 fast-spiking 和regular-spiking还有 bursting and stuttering神经元，当有恒定输入时，会产生一系列脉冲会周期的（bursting）或不周期的（stuttering）因为长间隔而产生中断。如图B
上图，快速脉冲（fast-spiking）神经元(A)在不适应的情况下有短的间隔时间间隔，而常规的脉冲神经元（C）表现适应，可见在间隔期间增加。许多神经元在抑制电流I1<0被终止后发出抑制反弹尖峰（D）

链接: 引用.
而GIF模型从这两个方面对LIF模型进行了update
对于GIF以及LIF之后会补充

欢迎关注我们！奇趣多多，数模多多！