AI 八数码A_star算法问题-实验报告

一 题目要求：

        八数码问题的A星搜索算法实现
        要求：设计估价函数，并采用c或python编程实现，以八数码为例演示A星算法的搜索过程，争取做到直观、清晰地演示算法，代码要适当加注释。
        八数码难题：在3×3方格棋盘上，分别放置了标有数字1,2,3,4,5,6,7,8的八张牌，初始状态S0可自己随机设定，使用的操作有:空格上移，空格左移，空格右移，空格下移。试采用A*算法编一程序实现这一搜索过程.

二 构造状态空间：

        这个题目的状态空间描述为一组整数对（r，s，t，u，v，w，x，y，z）。
        每个字母分别对应八数码的每个位置，如下表所示。

r	s	t
u	v	w
x	y	z

表1-八数码状态空间对应关系

三 对题目的理解：

        这个题目也应该采用树形结构来解，我觉得难点有二：

1. 如何建立每个节点的数据结构；
2. 因为是A*算法，所以公式f=g+h启发信息，如何在编程中体现。
   这里我是用Python写的算法，结点的数据结构如下：

class Point:
    def __init__(self, r, s, t, u, v, w, x, y, z):
        self.r = r
        self.s = s
        self.t = t
        self.u = u
        self.v = v
        self.w = w
        self.x = x
        self.y = y
        self.z = z
        self.g = 0
        self.f = 0  # f = g+h
        self.father = None
        self.node = [r, s, t, u, v, w, x, y, z]	

首先定义了八数码问题的9个位置的值。比较重要的是Point结点的father属性，指明了子节点与父节点的关系，保证了树形结构的准确性。然后定义了g属性，来保存节点的深度，f属性为g+h的和，这样就保证了启发信息。

3. 后来遇到个Python特有的bug，就是def了一个函数，然后传参，就算我用=号复制了一个list，原来的参数也会被改变，因为他们的指针都是一样的。解决方法是用copy.copy（list），这样复制就不是同一个指针了。

四 算法代码：

见报告最后。

五 代码解释：

1. 首先定义了open表、closed表，声明了Point类，定义了初始节点init（2, 0, 3, 1, 8, 4, 7, 6, 5）和目的节点（1, 2, 3, 8, 4, 5, 0, 7, 6）。
2. 在开始进行A_star（A*）算法之前，先定义几个函数：
   1） getKey：找出Point节点中0（即空格）的位置索引；
   2） up：空格上移函数。把某节点的空格和上方位置的值交换（考虑了溢出问题，即第一行不能up）；
   3） down：空格下移函数。同上；
   4） left：空格左移函数。同上；
   5） right：空格右移函数。同上；
   6） h：启发函数。将某个节点与目的节点比较，返回位置不同的数目；
   7） equal：判断两个节点是否相同；
   8） open_sort：把open表里面的节点，按照属性f的值，排序；
   9） in_list：判断节点是否在open表或者closed表已经存在。
3. 开始编写A*算法：
   1） 首先，先把初始节点init放入到OPEN表中，然后遍历OPEN表；
   2） 如果OPEN中取出的节点是目的节点goal，那么结束遍历；否则把这个节点从OPEN表取出，放入CLOUSED表；
   3） 然后根据此节点，来得到它的子节点，通过上、下、左、右四个方向来获取四个新节点，然后对四个节点遍历；
   4） 把该节点的f属性、father属性、g属性指定好。判断该new节点是否已经出现在open表中，如果已经出现了而且它的f属性值更好，说明它更优，那么把之前的移除，把这个插入。Open表同理。如果该new节点在open表和closed表都没有，那么把它直接插入到open表。最后根据f属性的值，对open表的节点排序。
   4 最后打印一下路径，就可显示出解。

六 算法输出分析：

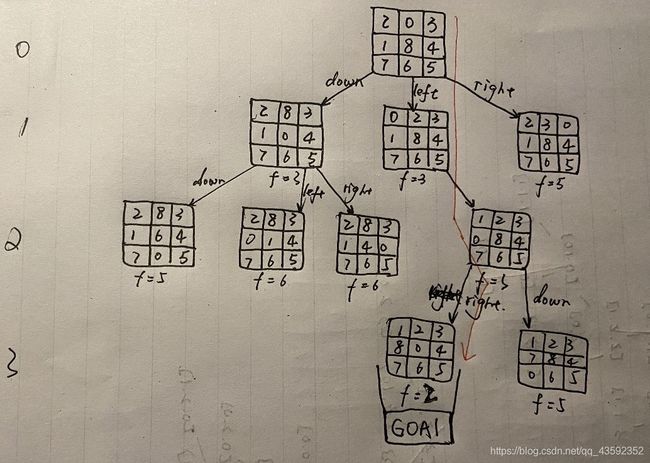
如图1是以初始节点init（2, 0, 3, 1, 8, 4, 7, 6, 5）和目的节点（1, 2, 3, 8, 4, 5, 0, 7, 6）运行的程序输出。根据OPEN表画出树形图如图2。

图1-程序输出

图2-分析过程

附：Python算法

import copy
import operator

OPEN = []  # open表
CLOSED = []  # closed表


class Point:
    def __init__(self, r, s, t, u, v, w, x, y, z):
        self.r = r
        self.s = s
        self.t = t
        self.u = u
        self.v = v
        self.w = w
        self.x = x
        self.y = y
        self.z = z
        self.g = 0
        self.f = 0  # f = g+h
        self.father = None
        self.node = [r, s, t, u, v, w, x, y, z]


init = Point(2, 0, 3, 1, 8, 4, 7, 6, 5)  # 初始节点
goal = Point(1, 2, 3, 8, 0, 4, 7, 6, 5)  # 目标


# 返回空位的index值
def getKey(s):
    return s.node.index(0)


def up(s, key):
    if key - 3 >= 0:
        arr = copy.copy(s.node)
        arr[key], arr[key - 3] = arr[key - 3], arr[key]
        return Point(arr[0], arr[1], arr[2], arr[3], arr[4], arr[5], arr[6], arr[7], arr[8])
    else:
        return None


def down(s, key):
    if key + 3 <= 8:
        arr = copy.copy(s.node)
        arr[key], arr[key + 3] = arr[key + 3], arr[key]
        return Point(arr[0], arr[1], arr[2], arr[3], arr[4], arr[5], arr[6], arr[7], arr[8])
    else:
        return None


def left(s, key):
    if key != 0 and key != 3 and key != 6:
        arr = copy.copy(s.node)
        arr[key], arr[key - 1] = arr[key - 1], arr[key]
        return Point(arr[0], arr[1], arr[2], arr[3], arr[4], arr[5], arr[6], arr[7], arr[8])
    else:
        return None


def right(s, key):
    if key != 2 and key != 5 and key != 8:
        arr = copy.copy(s.node)
        arr[key], arr[key + 1] = arr[key + 1], arr[key]
        return Point(arr[0], arr[1], arr[2], arr[3], arr[4], arr[5], arr[6], arr[7], arr[8])
    else:
        return None


# 启发函数
def h(s, p=goal):
    flag = 0
    for i in range(0, 9):
        if s.node[i] != p.node[i]:
            flag += 1
    return flag


def equal(a, b):
    if a.node == b.node:
        return True


# 将open_list以f值进行排序
def open_sort(l):
    the_key = operator.attrgetter('f')  # 指定属性排序的key
    l.sort(key=the_key)


# 扩展节点时在open表和closed表中找原来是否存在相同属性的节点
def in_list(new, l):
    for item in l:
        if new.node == item.node:
            return True, item
    return False, None


def A_star(s):
    global OPEN, CLOSED
    OPEN = [s]
    CLOSED = []

    while OPEN:  # open表非空
        get = OPEN[0]  # 取出open表第一个元素get
        if get.node == goal.node:  # 判断是否为目标节点
            return get
        OPEN.remove(get)  # 将get从open表移出
        CLOSED.append(get)  # 将get加入closed表
        # 以下得到一个get的新子节点new并考虑是否放入OPEN
        key = getKey(get)
        for i in range(0, 4):  # 四个方向
            if i == 0:
                new = up(get, key)
            elif i == 1:
                new = down(get, key)
            elif i == 2:
                new = left(get, key)
            elif i == 3:
                new = right(get, key)

            if new == None:  # 状态非法或new折返了
                pass
            # 如果要拓展的节点满足以上情况，将它的父亲设为当前节点，计算f，并对open_list排序
            else:
                new.father = get
                new.g = get.g + 1  # 与起点的距离
                new.f = get.g + h(new)  # f = g + h

                # 如果new在open表中(只关注m,c,b的值)
                if in_list(new, OPEN)[0]:
                    old = in_list(new, OPEN)[1]
                    if new.f < old.f:  # new的f
                        OPEN.remove(old)
                        OPEN.append(new)
                        open_sort(OPEN)
                    else:
                        pass
                # 继续，如果new在closed表中
                elif in_list(new, CLOSED)[0]:
                    old = in_list(new, CLOSED)[1]
                    if new.f < old.f:
                        # 将old从closed删除，并重新加入open
                        CLOSED.remove(old)
                        OPEN.append(new)
                        open_sort(OPEN)

                    else:
                        pass
                else:
                    OPEN.append(new)
                    open_sort(OPEN)
        print('OPEN:')
        for o in OPEN:
            print(o.node,o.f,o.g)


# 递归打印路径
def printPath(f):
    if f is None:
        return
    printPath(f.father)
    print(f.node)


if __name__ == '__main__':
    final = A_star(init)
    if final:
        print('有解，解为：')
        printPath(final)
    else:
        print('无解！')