关于作者
吴军,毕业于清华大学和约翰霍普金斯大学,他有很多个身份。
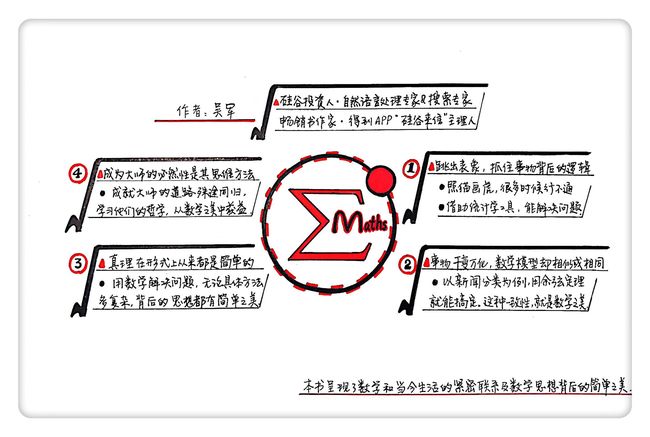
他是硅谷投资人,丰元资本的创始合伙人,是著名的自然语言处理专家和搜索专家,也是“得到”App专栏《硅谷来信》的主理人。他是谷歌的早期员工之一,在谷歌期间领导参与了很多研发项目,是谷歌中、日、韩搜索算法的发明人。同时他还是位畅销书作家,除了这本《数学之美》以外,还写过《文明之光》《智能时代》《浪潮之巅》等多本畅销书。
关于本书
在本书里,吴军从他的亲身经历出发,为我们介绍了数学在信息科学领域的种种应用,以及两位著名的数学信息科学大师的数学智慧。通过这些实际案例,他为我们展示了数学和我们当今生活的紧密联系,以及数学思想背后蕴含的简单之美。
核心内容
本书的核心思想是:数学和我们的生活联系非常紧密,生活中很多意想不到的问题,其实都能用数学方法来解决。数学能够帮助我们跳出问题的表面现象,抓住事物发展背后的逻辑,从而用一种巧妙的方法去解决复杂的问题;同时因为数学也具有简单的一致性,这就让我们经常能用一种思想来解决不同种类的问题。而数学之美,就体现在这种实用和简洁之中。
一、数学能帮我们跳出表象,抓住事物发展背后的逻辑
让计算机能处理人类的语言是我们今天很多工作的基础,所以科学家们很早就在这个问题上展开了研究。
其实最开始让计算机处理语言的时候,科学家们按照仿生学的思路,坚持认为,要让机器学会翻译或者语言识别,就必须像人一样,先让计算机学会语法。但是后来人们发现,语法规则实在是太多,根本没有办法穷尽。这种方法在上个世纪70年代逐渐被证明是不可行的。
与此同时,著名计算机科学家贾里尼克和他领导的实验室,发明了用统计学处理自然语言的方法,大大提高了语音识别的识别率和识别规模。他们的方法主要用了“马尔科夫假设”, 这个假设是说,假定一个句子里每一个词出现的概率,只和前一个词有关,就好比“涨停”这个词,最有可能出现在“股票”之后。那么,只要给计算机量足够大的机读文本,计算机就能算出来,在一个特定词后面出现某个词的概率。这样,只要把一句话里所有词出现的概率相乘,就是这个句子出现的概率了。概率最大的句子,就是我们需要的正确句子。
在解决问题时,过度地注意模仿却不懂变通,也是导致失败的重要原因。就像当年人们最开始制造飞机时,总是想把飞机的机翼设计成鸟的翅膀,但是最后莱特兄弟制造出来的第一架飞机,靠的不是仿生学,而是空气动力学。所以说,不被事情的表面现象迷惑,是一种很重要的能力,而数学就能帮我们跳出表象,抓住事物发展背后的逻辑。
二、数学的“一致性”体现着数学之美
余弦定理是一个揭示三角形边角关系的重要数学定理,使用余弦定理,就可以仅凭三角形两个边的向量,计算出这两个边的夹角。科学家为了让计算机能处理人类的语言,要先把新闻里的文字变成一组可以计算的数字,再设计一个算法,这样就能让计算机通过余弦定理,来算出任意两篇新闻的相似性,从而确定新闻的分类。
新闻里的词分为实词和虚词,“之乎者也的”这种虚词对判断新闻分类无益,就不考虑,而“股票”“利息”这种实词,对判断新闻分类很有帮助,是我们关注的重点,我们就要用这些实词计算出一则新闻的特征向量。只要给每一则新闻都计算出其独特的特征向量,再根据每一类新闻经常出现的词的特征,就可以判断出任意一条新闻的分类。
在新闻分类的工作中,计算机不需要去理解每篇新闻,只要找到同一类新闻的相似点就可以了,用余弦定理就能搞定,这就证明了数学的“一致性”。虽然事物发展千变万化,但处理它们的数学模型却是相似、甚至相同的。这种一致性,就是一种“数学之美”。
三、数学的妙处就是,一个好方法,常常也是最简单明了的方法
现在我们每个人几乎每天都会用到搜索引擎,它可以在极短的时间内搜索到大量你需要的网页,这背后的关键就是数学。
搜索引擎背后的基本数学原理,其实特别简单。二进制是世界上最简单的计数方法,因为二进制只有0和1两个数字,并且二进制还可以表示逻辑里的“是”和“非”。布尔运算,就是一种针对二进制的运算,它是19世纪英国的一名名叫布尔的数学家发明的,基本的运算只有“与”“或”“非”三种,非常简单。
搜索引擎会把用户查询的语句,转换成布尔运算的算式,看看搜索关键词有没有出现在这个网页,1就代表出现,0就代表没出现。这样一来,每个网页就会转换成一个数字。最后只要把显示为1的网页拿出来,就是你要的搜索结果了。计算机做布尔运算的速度非常快,所以搜索引擎可以轻松地在很短的时间里搜索出大量网页。
牛顿曾经说过,“真理在形式上从来都是简单的,而不是复杂和含混不清的”。数学之美也体现在这里,如果你能拿数学工具来解决问题,那么不管你的方法有多复杂,这里面的基本思想都应该是简单的。
四、两位数学信息科学大师的数学思维
本书的作者吴军认为,技术其实分为两种,分别是“术”和“道”。“术”指的是具体做事的技艺和方法,而“道”指的是做事的原理和原则。
这本书的目的是讲“道”,而不是去讲多么具体的“术”。因为很多具体的技术很快就会变得落伍。追求“术”的人,一辈子都会很辛苦。只有掌握了技术的本质和精髓,做事才能游刃有余。
第一位大师是阿米特·辛格。他是美国工程院院士,谷歌公司内的一位技术大神。辛格做事情的哲学,是先帮助用户解决80%的问题,再慢慢解决剩下20%的问题,这就让他总是能在较短的时间里较好的解决问题。阿米特·辛格还奉行简单的哲学,他认为最简单的东西往往是最好的。因为他认为越简单的事情越容易解释道理,这样可以方便查找错误。
第二位大师是迈克尔·柯林斯,他是一个擅长用数学把工作做到极致的人。柯林斯的哲学是追求极致和完美。比如他曾经设计了一个帮助计算机处理自然语言的分析器,目的不是为了验证什么理论,而仅仅是为了做出世界上最好的分析器。柯林斯的特点,就是把事情做到极致。他并不是刻意去追求繁琐和复杂,也不是和阿米特·辛格完全对立,他只是在追求数学上的严谨和完美。
不管是阿米特·辛格的简单哲学,还是迈克尔·柯林斯的完美哲学,都把数学的力量发挥到了极致,让数学用最好的方式来解决复杂的问题。这两种哲学,不是硬币的两面,而是相互补充的。
金句
1. 其实在解决问题时,过度地模仿却不懂变通,也是导致失败的重要原因。就像当年人们最开始制造飞机时,总是想把飞机的机翼设计成鸟的翅膀,通过上下摆动来起飞。但是最后莱特兄弟制造出来的第一架飞机,靠的不是仿生学,而是空气动力学。
2. 虽然事物发展千变万化,但处理它们的数学模型却是相似、甚至相同的,这种一致性,就是一种“数学之美”。
3. 牛顿曾经说过,“真理在形式上从来都是简单的,而不是复杂和含混不清的”,数学之美也体现在这里。如果你能拿数学工具来解决问题,那么不管你的方法有多复杂,这里面的基本思想都应该是简单的。
4. 追求“术”的人,一辈子都会很辛苦,只有掌握了技术的本质和精髓,做事才能游刃有余。
5. 很多人的失败,不是因为不优秀,而是方法不对,如果一开始就追求“高大全”,但是很长时间都不能解决问题,最后的结果反而会很差。