- 扫地机类清洁产品之直流无刷电机控制
悟空胆好小
清洁服务机器人单片机人工智能
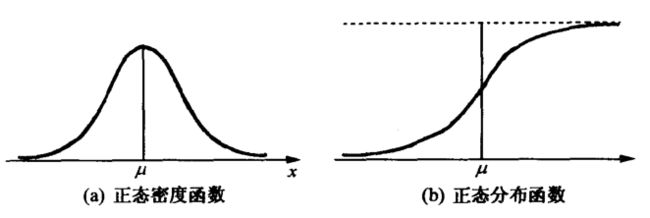
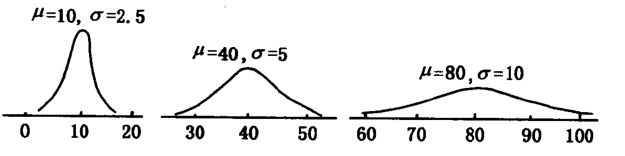
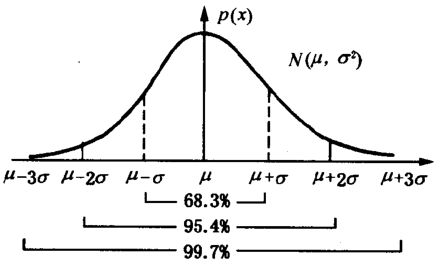
扫地机类清洁产品之直流无刷电机控制1.1前言扫地机产品有很多的电机控制,滚刷电机1个,边刷电机1-2个,清水泵电机,风机一个,部分中高端产品支持抹布功能,也就是存在抹布盘电机,还有追觅科沃斯石头等边刷抬升电机,滚刷抬升电机等的,这些电机有直流有刷电机,直接无刷电机,步进电机,电磁阀,挪动泵等不同类型。电机的原理,驱动控制方式也不行。接下来一段时间的几个文章会作个专题分析分享。直流有刷电机会自动持续
- 2018-07-23-催眠日作业-#不一样的31天#-66小鹿
小鹿_33
预言日:人总是在逃避命运的路上,与之不期而遇。心理学上有个著名的名词,叫做自证预言;经济学上也有一个很著名的定律叫做,墨菲定律;在灵修派上,还有一个很著名的法则,叫做吸引力法则。这3个领域的词,虽然看起来不太一样,但是他们都在告诉人们一个现象:你越担心什么,就越有可能会发生什么。同样的道理,你越想得到什么,就应该要积极地去创造什么。无论是自证预言,墨菲定律还是吸引力法则,对人都有正反2个维度的影响
- 《大清方方案》| 第二话
谁佐清欢
和珅究竟说了些什么?竟能令堂堂九五之尊龙颜失色!此处暂且按下不表;单说这位乾隆皇帝,果真不愧是康熙从小带过的,一旦决定了要做的事,便杀伐决断毫不含糊。他当即亲自拟旨,着令和珅为钦差大臣,全权负责处理方方事件,并钦赐尚方宝剑,遇急则三品以下官员可先斩后奏。和珅身负皇上重托,岂敢有半点怠慢,当夜即率领相关人等,马不停蹄杀奔江汉。这一路上,和珅的几位幕僚一直在商讨方方事件的处置方案。有位年轻幕僚建议快刀
- 《庄子.达生9》
钱江潮369
【原文】孔子观于吕梁,县水三十仞,流沫四十里,鼋鼍鱼鳖之所不能游也。见一丈夫游之,以为有苦而欲死也,使弟子并流而拯之。数百步而出,被发行歌而游于塘下。孔子从而问焉,曰:“吾以子为鬼,察子则人也。请问,‘蹈水有道乎’”曰:“亡,吾无道。吾始乎故,长乎性,成乎命。与齐俱入,与汩偕出,从水之道而不为私焉。此吾所以蹈之也。”孔子曰:“何谓始乎故,长乎性,成乎命?”曰:“吾生于陵而安于陵,故也;长于水而安于
- 高端密码学院笔记285
柚子_b4b4
高端幸福密码学院(高级班)幸福使者:李华第(598)期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲:刘莉一,知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫,目标永远下游。智者的梦再美,也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1,重视和珍惜的前提是知道它的价值非常重要,当你珍惜了,你就真正定下来,真正的学到身上。2,大家需要
- 2020-04-12每天三百字之连接与替代
冷眼看潮
不知道是不是好为人师,有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程,就是不断连接与替代的过程。人类发现了火并应用火以后,告别了茹毛饮血的野兽般的原始生活(火烧、烹饪替代了生食)人类用石器代替了完全手工,工具的使用使人类进步一大步。类似这样的替代还有很多,随着科技的发展,有更多的原始的事物被替代,代之以更高效、更先进的技术。在近现代,汽车替代了马车,高速公路和铁路
- 【加密社】Solidity 中的事件机制及其应用
加密社
闲侃区块链智能合约区块链
加密社引言在Solidity合约开发过程中,事件(Events)是一种非常重要的机制。它们不仅能够让开发者记录智能合约的重要状态变更,还能够让外部系统(如前端应用)监听这些状态的变化。本文将详细介绍Solidity中的事件机制以及如何利用不同的手段来触发、监听和获取这些事件。事件存储的地方当我们在Solidity合约中使用emit关键字触发事件时,该事件会被记录在区块链的交易收据中。具体而言,事件
- 东南林氏之九牧林候选父系
祖缘树TheYtree
渊源介绍东晋初年晋安林始祖林禄公入闽,传十世隋右丞林茂,由晋安迁居莆田北螺村。又五世而至林万宠,唐开元间任高平太守,生三子:韬、披、昌。韬公之孙攒,唐德宗立双阙以旌表其孝,时号"阙下林家"。昌公字茂吉,乃万宠公第三子,官兵部司马,配宋氏,生一子名萍。萍于唐贞元间明经及第,官沣洲司马(后追赠中宪大夫)。唐太和年间归隐后,迁居仙游游洋,世称“游洋林”;其后裔居游洋后迁移漳州漳浦路下,由路下林第四房平和
- 大伟说成语之唉声叹气
求索大伟
*大伟说成语*【唉声叹气】叹气:因心里不痛快或不如意而吐出长气,发出声音。因为痛苦、憋闷或感伤而发出叹息的声音。【大伟说】情绪外露,非人类所特有,动物亦有情绪,悲哀和欢乐所表示的情绪亦是不一样的,会嗷嗷大叫也会低吟痛哭。不同的是,人类的情绪更复杂,更多样,更丰富。唉声叹气,可以说是最基础的情绪,因为无奈而举足无措,不知该如何如何化解,只有独自一人慢慢承受,长吁短叹不知如何是好,其实是无能无力的表现
- libyuv之linux编译
jaronho
Linuxlinux运维服务器
文章目录一、下载源码二、编译源码三、注意事项1、银河麒麟系统(aarch64)(1)解决armv8-a+dotprod+i8mm指令集支持问题(2)解决armv9-a+sve2指令集支持问题一、下载源码到GitHub网站下载https://github.com/lemenkov/libyuv源码,或者用直接用git克隆到本地,如:gitclonehttps://github.com/lemenko
- 怎么做淘客赚钱(2022最新免费淘客盈利的方法)
高省_飞智666600
很多人都不知道什么是淘宝客,今天小编为大家解答一下吧。淘宝客,现在简称淘客,是时下比较流行的一个词语,特质为淘宝店推广商品获取提成的人,这些人没有自己的产品,只是在淘宝里面选择适合自己的产品,在自己比较熟悉的领域推广,把产品卖出去之后,会从淘宝店家那里获得百分之五到百分之五十左右的佣金。淘宝客付出的是什么呢?时间。你需要花时间去选适合自己推广的产品,需要花时间去选自己的推广方法,如果你打算自己做个
- Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
- 锁之缘
尘缘诗词原创作品
是谁追寻梦的足迹,是谁在偷偷的哭泣,日月隔离在黑白天地情感在心中蔓延的痕迹天与地的距离有多远流失的星晨落入哪片空间不要让泪水模糊双眼心牢中一样充满温暖谁说爱情没有永远白娘子又为何爱许仙蝴蝶墓地展翅翩翩轻歌慢舞袖卷人间传奇千古留爱万年…………月落星飞徘徊是选择不去问自已为合舍不得寂寞本就是痛苦的不在追寻梦中的痕迹才不会失去真实的自已
- ARM驱动学习之基础小知识
JT灬新一
ARM嵌入式arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购(能不能买到,价格)–原理图(涉及到稳定性)•layout画板工程师–layout(封装、布局,布线,log)(涉及到稳定性)–焊接的一部分工作(调试阶段板子的焊接)•驱动工程师–驱动,原理图,layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案,原理图(网表)–layout工程师(gerber文件)–PCB板
- ARM驱动学习之5 LEDS驱动
JT灬新一
嵌入式C底层arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点:•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点:DRIVER_NAME和DEVICE_NAME匹配。实现步骤:1.加入需要的头文件://Linux平台的gpio头文件#include//三
- ARM驱动学习之4小结
JT灬新一
嵌入式C++arm开发学习linux
ARM驱动学习之4小结#include#include#include#include#include#defineDEVICE_NAME"hello_ctl123"MODULE_LICENSE("DualBSD/GPL");MODULE_AUTHOR("TOPEET");staticlonghello_ioctl(structfile*file,unsignedintcmd,unsignedlo
- C++ | Leetcode C++题解之第409题最长回文串
Ddddddd_158
经验分享C++Leetcode题解
题目:题解:classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
- 2020-12-24
我和我的天使们
阅读《老子的心事》391—403“将欲取之,必固与之”:想要得到什么,首先就要送出什么。我常常对孩子们说,你希望别人怎样对你你就怎样对待别人。想要得到别人的尊重,首先要尊重别人。我希望她们可以不迟到,因为不迟到是对别人的尊重,我就自己就先做到不迟到。哪怕是约朋友逛街,我尽量准时赴约。我严格要求孩子们,也同样严格要求自己,我跟孩子们一起把好的品格变成习惯。“是谓微明”:这就是微妙的智慧。看起来很少很
- 18、架构-可观测性之聚合度量
大树~~
架构javapython后端架构
聚合度量聚合度量是指对系统运行时产生的各种指标数据进行收集、聚合和分析,以了解系统的健康状况和性能表现。聚合度量是可观测性的关键组成部分,通过对度量数据的分析,可以及时发现系统中的异常和瓶颈。以下是对聚合度量各个方面的详细解析,并结合具体的数据案例和技术支撑。指标收集收集系统运行时产生的各种指标数据是聚合度量的基础。常见的指标包括CPU使用率、内存使用率、请求处理时间、请求数、错误率等。以下是指标
- 学习“论语”-第59天
春峰轩
12.14子张问政。子曰:“居之无倦,行之以忠。”子张问为政之道。孔子说:“在位尽职不懈怠,执行政令要忠诚。”12.15子曰:“博学于文,约之以礼,亦可以弗畔矣夫!”孔子说:“君子广泛地学习文献,并且用礼节约束自己,也就不会离经叛道了。”12.16子曰:“君子成人之美,不成人之恶。小人反是。”孔子说:“君子成全别人的好事,而不助长别人的坏处。小人则与此相反行事。”知识点:“成人之美,不成人之恶”贯
- 2021-11-15
宙火
我给宋小姐写了首诗,是我在课上因思恋宋小姐而写的。“自古多情是唐宋,从来双飞归巢燕。邻家小女相聘婷,常使春意荡漾我。不知单思可为爱,惟愿一心付之汝。”我拿给宋小姐看了,她说我写得很棒。我很开心,但又不是那么开心。宋小姐是回复我了,但也只是说我写得很棒,对我诗句中蕴藏的真切感情,不知道是真的没发现,还是装作没发现。但我不深究,只是这样,我就很开心了。我答应宋小姐,一天给她写一首诗。
- 《我的青葱岁月之缘来是你》 第二章 迎新晚会
思源思缘思怨
“怎么你也来了这里?”我愉快的问到,想着这是上天给的缘分吗?我还没去找他竟然就相遇了。那个让我开心的老乡。“你好,我也是舞蹈社的新人啊!”他说,笑起来回答我,眼睛弯弯的。“这么巧,我叫吴倩,你叫啥?”“我叫韩欢,你也是B市人吧,c中毕业的?”“我不是,我是f中的,不然肯定会认识你的”“是吗?以后多多关照了”他还冲我眨了眨眼睛。内心一阵悸动,这是……回到寝室,我兴奋的告诉我的室友这个事情,我再次觉得
- 数据结构之哈希表
X同学的开始
数据结构数据结构散列表
哈希表(散列表)出现的原因在顺序表中查找时,需要从表头开始,依次遍历比较a[i]与key的值是否相等,直到相等才返回索引i;在有序表中查找时,我们经常使用的是二分查找,通过比较key与a[i]的大小来折半查找,直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是,这两种方法的效率都依赖于查找中比较的次数。我们有一种想法,能不能不经过比较,而是直接通过关键字key一次得到所要的结果呢?这时,
- 厦门自由行之第一天:
大苏子在广漂
厦门三人行之杂记出发前一天:12️28日下午15:00从广州粗发,来深圳集合!但是中间发生一个小插曲,验票时候发现车票不见了,或许也是一场恶作剧,对于不排队的人,忍不住说了一下,接下来就发现车票不见了,已经是拿在手上!不过还好,可以凭借购票订单查看到信息,所以有惊无险,顺利进站!晚上三个人一起去吃了柠檬鱼,说实话,那会,感觉美吃饱,啊哈哈!晚上回来,两个人又开始彻夜长谈,发现身边优秀的人,一大把,
- “这才好”麻辣香锅 能够增加人身体的免疫能力
小补文知
我就来介绍一种香锅,那就是“这才好”麻辣香锅,它产出于著名的蜀地文化,具有悠久的历史土家风味,麻辣鲜香,健康安全。采用传统秘制麻辣香锅油辣子,还有贴心加料“孜然包”满足人们的不同口味需求,香锅底料辣椒,微辣且香,含有丰富微量元素和维生素,具有辣而不躁,味道纯正,醇厚温和。花椒采用历史悠久,被列为宫廷供品的“贡椒”的汉源花椒。我们还挑选了“川菜之魂”郫县豆瓣的鼻祖品牌豆瓣,保留最原始的郫县豆瓣味道,
- 《太虚游》第六十二章。玄牝之威。
古楼臭道士
“好好好,流云这孩子深得我心,想必长爻知道是你的话定然会惊喜不已的。”白玄牝听得风流云应了下来,脸色慈和,伸手在他头顶轻轻抚了抚,如同抚在怀中九尾小狐一样自然,极其温柔。身后的四位青丘长老同时一怔,嘴角微动,似要开口劝阻。风流云只感到一道霞光瑞气如有实质一般顺着头顶百会大穴直沉在下丹田内,随后这股气息又逐渐凝聚,似乎给自己吃了什么东西一般。啊喔不好,这祖奶奶该不会是看中我这肉身,像人魔一样,要给她
- 生命如花
坦释空
每个人的心中都有一株妙莲花。这是禅家语。禅家总是站在理性的高处,以超越红尘的洒脱来参悟人生和自省生命。那么,凡俗中人呢?生如夏花之绚丽,死如秋叶之静美。这是诗人语。多少人在赞美:姑娘好像花一样!又有多少人在咏歌:花儿与少年。的确,人生如花。花一样的生命,理应自诞生之日起,就一瓣一瓣地绽放她的美丽与清香,使这个原本死寂荒凉的世界五彩缤纷,充满快乐。事实上,人类自诞生起,就一代一代地做着这方面的努力,
- 二婚到底是领证好还是不领证好?
孟妃青
伟人讲过,不以结婚为目的的谈恋爱,都是耍流氓!离婚了,再找对象,感情到了一定程度,领证结婚是水到渠成的事,再说我中华泱泱大国,有礼仪之邦的称谓,领证更是体现了尊重男女双方的行为。如果认为二婚就没必要领证了,只能说明,男女之间都暗藏心思,心不往一处走,日子过不好的。即便他们感情再深,都不是合法夫妻,只是名不正言不顺的同居关系。假如不要二人共同的孩子还好,就怕有了孩子,没领证,到时给孩子上户口都成问题
- 《华杉讲透王阳明传习录》
微微微微神
〔5〕希渊问:“圣人可学而至。然伯夷伊尹于孔子,才力终不同。其同谓之圣者安在”?先生曰,“圣人之所以为圣,只是其心纯乎天理,而无人欲之杂。犹精金之所以为精,但以其成色足而无铜铅之杂也。人到纯乎天理方是圣。金到足色方是精。然圣人之才力,亦有大小不同。犹金之分两有轻重。尧舜犹万镒。文王孔子犹九千镒。禹汤武王犹七八千镒。伯夷伊尹犹四五千镒。才力不同,而纯乎天理则同。皆可谓之圣人。犹分两虽不同,而足色则同
- “日舍一物”之42——活在当下,并向前看
記二十一
这件衣服已经有十五、六年了(突然发现我可真是能囤东西啊)。这原本是一件我非常喜欢的衣服,无论是样子,还是质地。照片拍的比较渣,但其实,白色棉质衣料中,尚织有银色的丝线,在阳光或灯光下,会闪亮,不晃眼,但很漂亮。或许正是因为太喜欢了,所以一直保留着,尽管很多年都没有再穿过了。因为不合适了。首先是随着年龄的增长,尽管体重总量没有太多变化(哦,其实还是涨了)。但是体型还是和十几年前不一样了,最明显的就是
- 多线程编程之理财
周凡杨
java多线程生产者消费者理财
现实生活中,我们一边工作,一边消费,正常情况下会把多余的钱存起来,比如存到余额宝,还可以多挣点钱,现在就有这个情况:我每月可以发工资20000万元 (暂定每月的1号),每月消费5000(租房+生活费)元(暂定每月的1号),其中租金是大头占90%,交房租的方式可以选择(一月一交,两月一交、三月一交),理财:1万元存余额宝一天可以赚1元钱,
- [Zookeeper学习笔记之三]Zookeeper会话超时机制
bit1129
zookeeper
首先,会话超时是由Zookeeper服务端通知客户端会话已经超时,客户端不能自行决定会话已经超时,不过客户端可以通过调用Zookeeper.close()主动的发起会话结束请求,如下的代码输出内容
Created /zoo-739160015
CONNECTEDCONNECTED
.............CONNECTEDCONNECTED
CONNECTEDCLOSEDCLOSED
- SecureCRT快捷键
daizj
secureCRT快捷键
ctrl + a : 移动光标到行首ctrl + e :移动光标到行尾crtl + b: 光标前移1个字符crtl + f: 光标后移1个字符crtl + h : 删除光标之前的一个字符ctrl + d :删除光标之后的一个字符crtl + k :删除光标到行尾所有字符crtl + u : 删除光标至行首所有字符crtl + w: 删除光标至行首
- Java 子类与父类这间的转换
周凡杨
java 父类与子类的转换
最近同事调的一个服务报错,查看后是日期之间转换出的问题。代码里是把 java.sql.Date 类型的对象 强制转换为 java.sql.Timestamp 类型的对象。报java.lang.ClassCastException。
代码:
- 可视化swing界面编辑
朱辉辉33
eclipseswing
今天发现了一个WindowBuilder插件,功能好强大,啊哈哈,从此告别手动编辑swing界面代码,直接像VB那样编辑界面,代码会自动生成。
首先在Eclipse中点击help,选择Install New Software,然后在Work with中输入WindowBui
- web报表工具FineReport常用函数的用法总结(文本函数)
老A不折腾
finereportweb报表工具报表软件java报表
文本函数
CHAR
CHAR(number):根据指定数字返回对应的字符。CHAR函数可将计算机其他类型的数字代码转换为字符。
Number:用于指定字符的数字,介于1Number:用于指定字符的数字,介于165535之间(包括1和65535)。
示例:
CHAR(88)等于“X”。
CHAR(45)等于“-”。
CODE
CODE(text):计算文本串中第一个字
- mysql安装出错
林鹤霄
mysql安装
[root@localhost ~]# rpm -ivh MySQL-server-5.5.24-1.linux2.6.x86_64.rpm Preparing... #####################
- linux下编译libuv
aigo
libuv
下载最新版本的libuv源码,解压后执行:
./autogen.sh
这时会提醒找不到automake命令,通过一下命令执行安装(redhat系用yum,Debian系用apt-get):
# yum -y install automake
# yum -y install libtool
如果提示错误:make: *** No targe
- 中国行政区数据及三级联动菜单
alxw4616
近期做项目需要三级联动菜单,上网查了半天竟然没有发现一个能直接用的!
呵呵,都要自己填数据....我了个去这东西麻烦就麻烦的数据上.
哎,自己没办法动手写吧.
现将这些数据共享出了,以方便大家.嗯,代码也可以直接使用
文件说明
lib\area.sql -- 县及县以上行政区划分代码(截止2013年8月31日)来源:国家统计局 发布时间:2014-01-17 15:0
- 哈夫曼加密文件
百合不是茶
哈夫曼压缩哈夫曼加密二叉树
在上一篇介绍过哈夫曼编码的基础知识,下面就直接介绍使用哈夫曼编码怎么来做文件加密或者压缩与解压的软件,对于新手来是有点难度的,主要还是要理清楚步骤;
加密步骤:
1,统计文件中字节出现的次数,作为权值
2,创建节点和哈夫曼树
3,得到每个子节点01串
4,使用哈夫曼编码表示每个字节
- JDK1.5 Cyclicbarrier实例
bijian1013
javathreadjava多线程Cyclicbarrier
CyclicBarrier类
一个同步辅助类,它允许一组线程互相等待,直到到达某个公共屏障点 (common barrier point)。在涉及一组固定大小的线程的程序中,这些线程必须不时地互相等待,此时 CyclicBarrier 很有用。因为该 barrier 在释放等待线程后可以重用,所以称它为循环的 barrier。
CyclicBarrier支持一个可选的 Runnable 命令,
- 九项重要的职业规划
bijian1013
工作学习
一. 学习的步伐不停止 古人说,活到老,学到老。终身学习应该是您的座右铭。 世界在不断变化,每个人都在寻找各自的事业途径。 您只有保证了足够的技能储
- 【Java范型四】范型方法
bit1129
java
范型参数不仅仅可以用于类型的声明上,例如
package com.tom.lang.generics;
import java.util.List;
public class Generics<T> {
private T value;
public Generics(T value) {
this.value =
- 【Hadoop十三】HDFS Java API基本操作
bit1129
hadoop
package com.examples.hadoop;
import org.apache.hadoop.conf.Configuration;
import org.apache.hadoop.fs.FSDataInputStream;
import org.apache.hadoop.fs.FileStatus;
import org.apache.hadoo
- ua实现split字符串分隔
ronin47
lua split
LUA并不象其它许多"大而全"的语言那样,包括很多功能,比如网络通讯、图形界面等。但是LUA可以很容易地被扩展:由宿主语言(通常是C或 C++)提供这些功能,LUA可以使用它们,就像是本来就内置的功能一样。LUA只包括一个精简的核心和最基本的库。这使得LUA体积小、启动速度快,从 而适合嵌入在别的程序里。因此在lua中并没有其他语言那样多的系统函数。习惯了其他语言的字符串分割函
- java-从先序遍历和中序遍历重建二叉树
bylijinnan
java
public class BuildTreePreOrderInOrder {
/**
* Build Binary Tree from PreOrder and InOrder
* _______7______
/ \
__10__ ___2
/ \ /
4
- openfire开发指南《连接和登陆》
开窍的石头
openfire开发指南smack
第一步
官网下载smack.jar包
下载地址:http://www.igniterealtime.org/downloads/index.jsp#smack
第二步
把smack里边的jar导入你新建的java项目中
开始编写smack连接openfire代码
p
- [移动通讯]手机后盖应该按需要能够随时开启
comsci
移动
看到新的手机,很多由金属材质做的外壳,内存和闪存容量越来越大,CPU速度越来越快,对于这些改进,我们非常高兴,也非常欢迎
但是,对于手机的新设计,有几点我们也要注意
第一:手机的后盖应该能够被用户自行取下来,手机的电池的可更换性应该是必须保留的设计,
- 20款国外知名的php开源cms系统
cuiyadll
cms
内容管理系统,简称CMS,是一种简易的发布和管理新闻的程序。用户可以在后端管理系统中发布,编辑和删除文章,即使您不需要懂得HTML和其他脚本语言,这就是CMS的优点。
在这里我决定介绍20款目前国外市面上最流行的开源的PHP内容管理系统,以便没有PHP知识的读者也可以通过国外内容管理系统建立自己的网站。
1. Wordpress
WordPress的是一个功能强大且易于使用的内容管
- Java生成全局唯一标识符
darrenzhu
javauuiduniqueidentifierid
How to generate a globally unique identifier in Java
http://stackoverflow.com/questions/21536572/generate-unique-id-in-java-to-label-groups-of-related-entries-in-a-log
http://stackoverflow
- php安装模块检测是否已安装过, 使用的SQL语句
dcj3sjt126com
sql
SHOW [FULL] TABLES [FROM db_name] [LIKE 'pattern']
SHOW TABLES列举了给定数据库中的非TEMPORARY表。您也可以使用mysqlshow db_name命令得到此清单。
本命令也列举数据库中的其它视图。支持FULL修改符,这样SHOW FULL TABLES就可以显示第二个输出列。对于一个表,第二列的值为BASE T
- 5天学会一种 web 开发框架
dcj3sjt126com
Web框架framework
web framework层出不穷,特别是ruby/python,各有10+个,php/java也是一大堆 根据我自己的经验写了一个to do list,按照这个清单,一条一条的学习,事半功倍,很快就能掌握 一共25条,即便很磨蹭,2小时也能搞定一条,25*2=50。只需要50小时就能掌握任意一种web框架
各类web框架大同小异:现代web开发框架的6大元素,把握主线,就不会迷路
建议把本文
- Gson使用三(Map集合的处理,一对多处理)
eksliang
jsongsonGson mapGson 集合处理
转载请出自出处:http://eksliang.iteye.com/blog/2175532 一、概述
Map保存的是键值对的形式,Json的格式也是键值对的,所以正常情况下,map跟json之间的转换应当是理所当然的事情。 二、Map参考实例
package com.ickes.json;
import java.lang.refl
- cordova实现“再点击一次退出”效果
gundumw100
android
基本的写法如下:
document.addEventListener("deviceready", onDeviceReady, false);
function onDeviceReady() {
//navigator.splashscreen.hide();
document.addEventListener("b
- openldap configuration leaning note
iwindyforest
configuration
hostname // to display the computer name
hostname <changed name> // to change
go to: /etc/sysconfig/network, add/modify HOSTNAME=NEWNAME to change permenately
dont forget to change /etc/hosts
- Nullability and Objective-C
啸笑天
Objective-C
https://developer.apple.com/swift/blog/?id=25
http://www.cocoachina.com/ios/20150601/11989.html
http://blog.csdn.net/zhangao0086/article/details/44409913
http://blog.sunnyxx
- jsp中实现参数隐藏的两种方法
macroli
JavaScriptjsp
在一个JSP页面有一个链接,//确定是一个链接?点击弹出一个页面,需要传给这个页面一些参数。//正常的方法是设置弹出页面的src="***.do?p1=aaa&p2=bbb&p3=ccc"//确定目标URL是Action来处理?但是这样会在页面上看到传过来的参数,可能会不安全。要求实现src="***.do",参数通过其他方法传!//////
- Bootstrap A标签关闭modal并打开新的链接解决方案
qiaolevip
每天进步一点点学习永无止境bootstrap纵观千象
Bootstrap里面的js modal控件使用起来很方便,关闭也很简单。只需添加标签 data-dismiss="modal" 即可。
可是偏偏有时候需要a标签既要关闭modal,有要打开新的链接,尝试多种方法未果。只好使用原始js来控制。
<a href="#/group-buy" class="btn bt
- 二维数组在Java和C中的区别
流淚的芥末
javac二维数组数组
Java代码:
public class test03 {
public static void main(String[] args) {
int[][] a = {{1},{2,3},{4,5,6}};
System.out.println(a[0][1]);
}
}
运行结果:
Exception in thread "mai
- systemctl命令用法
wmlJava
linuxsystemctl
对比表,以 apache / httpd 为例 任务 旧指令 新指令 使某服务自动启动 chkconfig --level 3 httpd on systemctl enable httpd.service 使某服务不自动启动 chkconfig --level 3 httpd off systemctl disable httpd.service 检查服务状态 service h