小白都能理解的ROC曲线与AUC值
项目github地址:bitcarmanlee easy-algorithm-interview-and-practice
欢迎大家star,留言,一起学习进步
1.ROC曲线
在信号检测理论中,接收者操作特征曲线(receiver operating characteristic curve,或者叫ROC曲线)是一种坐标图式的分析工具,用于 (1) 选择最佳的信号侦测模型、舍弃次佳的模型。 (2) 在同一模型中设定最佳阈值。
在做决策时,ROC分析能不受成本/效益的影响,给出客观中立的建议。
ROC曲线首先是由二战中的电子工程师和雷达工程师发明的,用来侦测战场上的敌军载具(飞机、船舰),也就是信号检测理论。之后很快就被引入了心理学来进行信号的知觉检测。数十年来,ROC分析被用于医学、无线电、生物学、犯罪心理学领域中,而且最近在机器学习(machine learning)和数据挖掘(data mining)领域也得到了很好的发展。(参考文献1)
2.ROC曲线解释
一个二分类问题,可以将实例分成正类(postive)或者负类(negative)。但是实际中分类时,会出现四种情况
1.某一个实例是正类,并且预测结果也为正类,此为真正类(True Positive, TP)
2.某一个实例是正类,被预测为负类,此为假负类(False Negative, FN)
3.某一个实例是负类,被预测为正类,此为假正类(False Positive, FP)
4.某一个实例为负类,并且预测结果也为负类,此为真负类(True Negative, TN)
ROC曲线的纵坐标是真正率(TPR)
T P R = T P T P + F N TPR = \frac{TP}{TP + FN} TPR=TP+FNTP
用通俗的语言解释就是预测的正例中,实际上也为正的在所有正例中的占比,这个比例自然是越大越好。
ROC曲线的横坐标是假正率(FPR)
F P R = F P F P + T N FPR = \frac{FP}{FP + TN} FPR=FP+TNFP
用通俗的语言解释就是预测的正例中,实际上为负的在所有负例中的占比。这个比例是越小越好。
很明显,这两个指标是互斥的,无法同时达到最优效果。
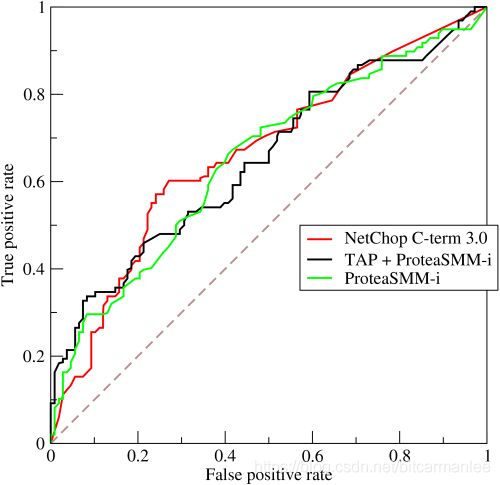
图片来自wiki百科。
3.ROC曲线中的两个特殊点
上面曲线中有两个特殊点(0,0), (1,1)
其中(0,0)点表示TPR,FPR均为0。此时阈值无为无穷大,所有样本被预测为负类,TP = 0, FP = 0,样本的预测结果只能是TN或者FN,所以TPR=FPR=0。
其中(1,1)点表示TPR, FPR均为1。此时阈值为0,所有样本被与预测为正类,样本的预测结果只能为TP或者FP,TN或者FN均为0,所以TPR = TP / (TP + FN) = 1,FPR同样为1。
4.如何画ROC曲线
假设已经得出一系列样本被划分为正类的概率,然后按照大小排序,下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。
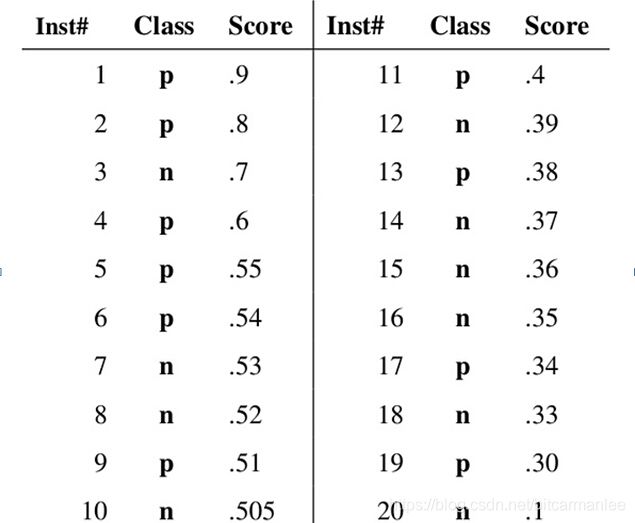
接下来,我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
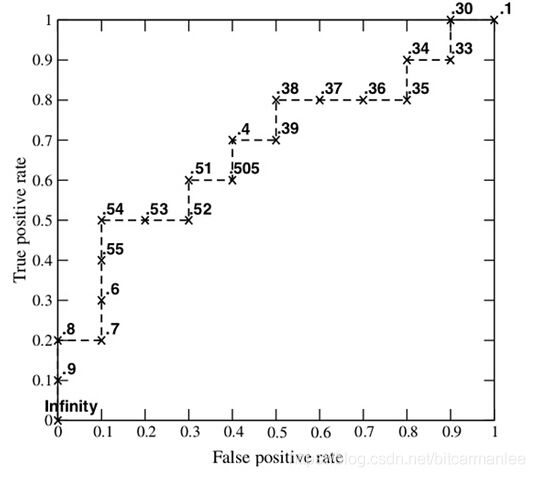
(以上例子来自网络)
5.AUC值的含义
AUC值指的是ROC曲线下的面积。AUC常常被用来作为模型排序好坏的指标,原因在于AUC可以看做随机从正负样本中选取一对正负样本,其中正样本的得分大于负样本的概率。所以,AUC常用在排序场景的模型评估,比如搜索和推荐等场景。
6.AUC的计算方法
在有M个正样本,N个负样本的数据集里。一共有MN对样本(一对样本即,一个正样本与一个负样本)。统计这MN对样本里,正样本的预测概率大于负样本的预测概率的个数。
∑ I ( P 正 , P 负 ) M ∗ N \frac{\sum I(P_{正}, P_负)}{M*N} M∗N∑I(P正,P负)
其中,
I ( P 正 , P 负 ) = { 1 , P 正 > P 负 0.5 , P 正 = P 负 0 , P 正 < P 负 I(P_{正}, P_负)=\left\{ \begin{aligned} 1, P_正>P_负 \\ 0.5,P_正=P_负 \\ 0,P_正
举个例子来看:
| index | label | pro |
|---|---|---|
| A | 0 | 0.1 |
| B | 0 | 0.5 |
| C | 1 | 0.3 |
| D | 1 | 0.7 |
上面的例子有4个样本,其中两个为正两个为负,则M*N=4,总共4个样本对。
(D,B), (D,A), (C,B), (C,A)
其中,I(D,B)=I(D,A)=I(C,A)=1, I(C,B)=0
最后AUC的值为(1+1+1+0)/4 = 0.75
参考文献
1.https://zh.wikipedia.org/wiki/ROC%E6%9B%B2%E7%BA%BF