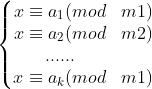中国剩余定理 (孙子定理) 的证明和代码

目录

【引入】

【中国剩余定理】

【代码实现】

【借鉴于】

---

【引入】

《孙子算经》里有这样一个题目：今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

术曰：“三、三数之剩二，置一百四十；五、五数之剩三，置六十三；七、七数之剩二，置三十，并之，得二百三十三。以二百一十减之，即得。凡三、三数之剩一，则置七十；五、五数之剩一，则置二十一；七、七数之剩一，则置十五。一百六以上，一百五减之，即得。”

意思是有一堆东西不知道具体数目，3个3个数剩2个，5个5个数剩3个，7个7个数剩2个，问一共有多少个。

答案：

计算思路如下：

70是能被5和7整除的且除以3余1的数字，21是能被3和7整除且除以5余1的数字，15是能被3或5整除且除以7余1的数字。

所以如果有数   (N,N1,N2,N3均为正整数)，则整数N是符合题目要求的结果。

我们将N1赋值2，N2赋值3，N3赋值2，则:  。

但是3，5，7的最小公倍数为105，所以N + 105*M均为正解。因此最小正整数解就是(N mod 105)也就是23。

中国剩余定理就是这个题目的一般情况。

【中国剩余定理】

内容：设m1,m2...mk是两两互素的正整数，则同余方程组:    

存在唯一最小整数解使得方程成立。

模仿上面的解题过程，首先我们假设  就是对应的数字，满足以下条件:

N1 能够被 m2, m3..., mk整除，而且除以m1正好余1.

N2 能够被 m1, m3..., mk整除，而且除以m2正好余1.

...............................

Nk能够被m1, m2,...,mk-1整除，而且除以mk正好余1.

求出这些数字之后，我们假设  就是我们要求的  的一个解，

那么同上， 就是  的最小正整数解。为什么要加上一个余数的乘积呢，因为X可能为负数，且加上整数个模数再取模对结果不产生任何影响。

那么， 怎么求呢？

我们令  ，因为  ，不包括  ，所以  ，为任意整数。

又  ，所以  ，B为任意整数。

综上所述， 

因为  都是互质数，所以  与  也互质，即  

也就是说： ，其中唯一未知数只有A和B，这就是经典拓展欧几里得定理的原型，按照拓展欧几里得定理求解即可得到A和B。

扩展欧几里德定理用于在已知a,b求解一对x,y使得a*x+b*y=gcd(a,b)，常用于求解模线性方程及方程组中。

int exgcd(int a, int b, int &x, int &y)
{
　　if(b == 0){
　　   x = 1; y = 0;
　　   return a;
　　}
　　int r = exgcd(b, a % b, x, y);
　　int t = x;
　　x = y;
　　y = t - a / b * y;
　　return r;
}

我们要求的A和B就相当于要求解的一对(x,y)

【代码实现】

模数互质：

#include 
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
    if(!b){
        x=1,y=0;
        return a;
    }
    int ret=exgcd(b,a%b,x,y);
    int t=x;
    x=y,y=t-a/b*y;
    return ret;
}
int china(int a[],int m[],int k){
    int M=1,ans=0;
    for(int i=0;i

模数不一定互质：

例题：poj2891

#include
using namespace std;
typedef long long LL;
const int maxn=1e5+10;
LL a[maxn],r[maxn];
int n;
LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(b==0){
        x=1;y=0;
        return a;
    }
    LL d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
LL china()
{
    LL a1,r1,a2,r2,x,y;
    a1=a[1],r1=r[1];
    for(int i=2;i<=n;i++){
        a2=a[i];r2=r[i];
        LL c=r2-r1;
        LL d=exgcd(a1,a2,x,y);
        if(c%d) return -1;
        LL x0=c/d*x;
        LL t=a2/d;
        x0=(x0%t+t)%t;
        r1=r1+a1*x0;
        a1=a1/d*a2;
    }
    return r1;
}
int main()
{
     while(~scanf("%d",&n)){
        for(int i=1;i<=n;i++)
            scanf("%lld%lld",&a[i],&r[i]);
        printf("%lld\n",china());
    }
    return 0;
}

适用于模数比较小的构造法：构造满足前i个同余方程的最小自然数解。假设前i-1个方程的最小自然数解为f(i-1)，lcm(p1,p2,…,pi-1)=y，则求解f(i)时，令f(i)=f(i-1)，然后让f(i)每次加上y，直到满足第i个方程为止。可以证明，在保证有解的情况下，加法运算不会超过pi次。 

实现见：Han Xin and His Troops（中国剩余定理 or 构造）
 

【借鉴于】

中国剩余定理