【详解+推导!!】PPO 近端策略优化
近端策略优化(PPO, Proximal Policy Optimization)是强化学习中十分重要的一种算法,被 OpenAI 作为默认强化学习算法,在多种强化学习应用中表现十分优异。
文章目录
- 1. From On-policy to Off-policy
- 2. Importance Sampling
- 3. 推导off-policy下的梯度公式
- 4. TRPO和PPO
- 5. PPO2
1. From On-policy to Off-policy
- 如果被训练的agent和与环境做互动的agent(生成训练样本)是同一个的话,那么叫做on-policy(同策略)。
- 如果被训练的agent和与环境做互动的agent(生成训练样本)不是同一个的话,那么叫做off-policy(异策略)。
换一种拟人的方式来讲:
- on-policy:我们来学习下象棋,先和大家下若干把棋,然后总结经验提升自己,成为2.0的自己。2.0的自己再和大家下棋,再总结2.0期间下过棋局的经验,成为3.0的自己,以此类推。其中关键点在于,2.0升级到3.0的过程中不能利用1.0时的下棋经验。
- off-policy:与on-policy不同的是我们,我们可以反复利用1.0期间的下棋经验,从2.0升级到3.0再升级到4.0,等等。甚至我们还可以用其他人的下棋经验提升自己。
为什么要考虑使用Off-policy?
我们可以回顾Policy Gradient的过程,Policy Gradient是一种on-policy的方法,他首先要利用现有策略和环境互动,产生学习资料(决策数据 τ \tau τ),然后利用产生的资料,按照Policy Gradient的方法更新策略参数。然后再用新的策略去交互、更新、交互、更新,如此重复。这其中有很多的时间都浪费在了产生资料的过程中,Off-Policy的目的就是更加充分的利用actor产生的交互资料,增加学习效率。
2. Importance Sampling
为什么要使用Importance Sampling呢?
我们可以看一下Policy Gradient的梯度公式:
∇ R ˉ ( τ ) = E τ ~ p θ ( τ ) [ A θ ( s t , a t ) ∇ l o g p θ ( a t n ∣ s t n ) ] \nabla\bar{R}(\tau) = E_{\tau~p_\theta(\tau)}[A^\theta(s_t, a_t)\nabla log p_\theta(a_t^n|s_t^n) ] ∇Rˉ(τ)=Eτ~pθ(τ)[Aθ(st,at)∇logpθ(atn∣stn)]
问题在于上面的式子是基于 τ ~ p θ ( τ ) \tau~p_\theta(\tau) τ~pθ(τ)采样的,一旦更新了参数,从 θ \theta θ到 θ ′ \theta' θ′,这个概率 P θ P_{\theta} Pθ就不对了。而Importance Sampling解决的正是从 τ ~ p θ ( τ ) \tau~p_\theta(\tau) τ~pθ(τ)采样,计算 θ ′ \theta' θ′的 ∇ R ˉ ( τ ) \nabla\bar{R}(\tau) ∇Rˉ(τ)的问题。
重要性采样(Importance Sampling)的推导可以点击链接查看,这里直接给出公式:
E x ~ p [ f ( x ) ] = ∫ f ( x ) p ( x ) d x = ∫ f ( x ) p ( x ) q ( x ) q ( x ) d x = E x ~ q [ f ( x ) p ( x ) q ( x ) ] E_{x~p}[f(x)] = \int f(x)p(x)dx = \int f(x) \frac{p(x)}{q(x)}q(x)dx = E_{x~q}[f(x) \frac{p(x)}{q(x)}] Ex~p[f(x)]=∫f(x)p(x)dx=∫f(x)q(x)p(x)q(x)dx=Ex~q[f(x)q(x)p(x)]
上面的式子表示,已知 x x x服从分布 p p p,我们要计算 f ( x ) f(x) f(x),但是 p p p不方便采样,我们就可以通过 q q q去采样,计算期望。
E x ~ q [ f ( x ) p ( x ) q ( x ) ] E_{x~q}[f(x) \frac{p(x)}{q(x)}] Ex~q[f(x)q(x)p(x)]
这里我们用 q q q做采样, p ( x ) q ( x ) \frac{p(x)}{q(x)} q(x)p(x)叫做重要性权重,用来修正 q q q与 p p p两个分布的差异。理论上利用重要性采样的方法我们可以用任何 q q q来完成采样,但是由于采样数量的限制, q q q与 p p p的差异不能太大。如果差异过大, E x ~ q [ f ( x ) p ( x ) q ( x ) ] E_{x~q}[f(x) \frac{p(x)}{q(x)}] Ex~q[f(x)q(x)p(x)]与 E x ~ p [ f ( x ) ] E_{x~p}[f(x)] Ex~p[f(x)]的差异也会很大。
3. 推导off-policy下的梯度公式
在on-policy情况下,Policy Gradient公式为:
∇ R ˉ ( τ ) = E ( s t , a t ) ~ π θ [ A θ ( s t , a t ) ∇ l o g p θ ( a t n ∣ s t n ) ] \nabla\bar{R}(\tau) = E_{(s_t,a_t)~\pi_\theta}[A^\theta(s_t, a_t)\nabla log p_\theta(a_t^n|s_t^n) ] ∇Rˉ(τ)=E(st,at)~πθ[Aθ(st,at)∇logpθ(atn∣stn)]
由上面的推导可得,我们利用 θ ′ \theta' θ′采样,优化 θ \theta θ时的公式为:
∇ R ˉ ( τ ) = E ( s t , a t ) ~ π θ ′ [ p θ ( s t , a t ) p θ ′ ( s t , a t ) A θ ( s t , a t ) ∇ l o g p θ ( a t n ∣ s t n ) ] \nabla\bar{R}(\tau) = E_{(s_t,a_t)~\pi_{\theta'}}[\frac{p_{\theta(s_t,a_t)}}{p_{\theta'(s_t,a_t)}}A^{\theta}(s_t, a_t)\nabla log p_\theta(a_t^n|s_t^n) ] ∇Rˉ(τ)=E(st,at)~πθ′[pθ′(st,at)pθ(st,at)Aθ(st,at)∇logpθ(atn∣stn)]
其中 A θ ( s t , a t ) A^{\theta}(s_t, a_t) Aθ(st,at)为比较优势,从该项的推导过程可以知道,它是由采样样本决定的,所以应该用 A θ ′ ( s t , a t ) A^{\theta'}(s_t, a_t) Aθ′(st,at)表示,所以式子变为:
∇ R ˉ ( τ ) = E ( s t , a t ) ~ π θ ′ [ p θ ( s t , a t ) p θ ′ ( s t , a t ) A θ ′ ( s t , a t ) ∇ l o g p θ ( a t n ∣ s t n ) ] \nabla\bar{R}(\tau) = E_{(s_t,a_t)~\pi_{\theta'}}[\frac{p_{\theta(s_t,a_t)}}{p_{\theta'(s_t,a_t)}}A^{\theta'}(s_t, a_t)\nabla log p_\theta(a_t^n|s_t^n) ] ∇Rˉ(τ)=E(st,at)~πθ′[pθ′(st,at)pθ(st,at)Aθ′(st,at)∇logpθ(atn∣stn)]
将 p θ ( s t , a t ) p_{\theta(s_t,a_t)} pθ(st,at)展开可得:
∇ R ˉ ( τ ) = E ( s t , a t ) ~ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) p θ ( s t ) p θ ′ ( s t ) A θ ′ ( s t , a t ) ∇ l o g p θ ( a t n ∣ s t n ) ] \nabla\bar{R}(\tau) = E_{(s_t,a_t)~\pi_{\theta'}}[ \frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}} \frac{p_{\theta(s_t)}}{p_{\theta'(s_t)}} A^{\theta'}(s_t, a_t)\nabla log p_\theta(a_t^n|s_t^n) ] ∇Rˉ(τ)=E(st,at)~πθ′[pθ′(at∣st)pθ(at∣st)pθ′(st)pθ(st)Aθ′(st,at)∇logpθ(atn∣stn)]
我们认为某一个状态 s t s_t st出现的概率与策略函数无关,只与环境有关,所以可以认为 p θ ( s t ) ≈ p θ ′ ( s t ) p_{\theta(s_t)} \approx p_{\theta'(s_t)} pθ(st)≈pθ′(st),由此得出如下公式:
∇ R ˉ ( τ ) = E ( s t , a t ) ~ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ∇ l o g p θ ( a t n ∣ s t n ) ] \nabla\bar{R}(\tau) = E_{(s_t,a_t)~\pi_{\theta'}}[ \frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}} A^{\theta'}(s_t, a_t)\nabla log p_\theta(a_t^n|s_t^n) ] ∇Rˉ(τ)=E(st,at)~πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)∇logpθ(atn∣stn)]
根据上面的式子,我们就可以完成off-policy的工作,反推出目标函数为:
J θ ′ ( θ ) = E ( s t , a t ) ~ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] J^{\theta'}(\theta) = E_{(s_t,a_t)~\pi_{\theta'}}[ \frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}} A^{\theta'}(s_t, a_t)] Jθ′(θ)=E(st,at)~πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)]
J θ ′ ( θ ) J^{\theta'}(\theta) Jθ′(θ)中括号里的 θ \theta θ表示我们要优化的参数, θ ′ \theta' θ′表示实际和环境互动产生样本的Actor的参数,在计算过程中 p θ ′ ( a t ∣ s t ) p_{\theta'(a_t|s_t)} pθ′(at∣st)和 A θ ′ ( s t , a t ) A^{\theta'}(s_t, a_t) Aθ′(st,at)都是根据样本计算出的常数,所以也很好理解,我们优化的目标就是 p θ ( a t ∣ s t ) p_{\theta(a_t|s_t)} pθ(at∣st)。
4. TRPO和PPO
TRPO
TRPO是PPO的前身,叫做信任区域策略优化(Trust Region Policy Optimization)。其思路如下:优化目标就是我们上面推出的 J θ ′ ( θ ) J^{\theta'}(\theta) Jθ′(θ),但是我们使用了重要性采样,而重要性采样的要求就是原采样和目标采样不能相差太大,这里就是指 π θ \pi_{\theta} πθ和 π θ ′ \pi_{\theta'} πθ′输出的动作不能相差太大。TRPO采用KL散度(KL divergence)的方法来评价二者的差异,记作 K L ( θ , θ ′ ) KL(\theta, \theta') KL(θ,θ′)。算法规定,当进行优化时, K L ( θ , θ ′ ) KL(\theta, \theta') KL(θ,θ′)要小于一个阈值 σ \sigma σ,TRPO公式如下:
J T R P O θ ′ ( θ ) = E ( s t , a t ) ~ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] , K L ( θ , θ ′ ) < σ J_{TRPO}^{\theta'}(\theta) = E_{(s_t,a_t)~\pi_{\theta'}}[ \frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}} A^{\theta'}(s_t, a_t)],KL(\theta, \theta')<\sigma JTRPOθ′(θ)=E(st,at)~πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)],KL(θ,θ′)<σ
PPO
TRPO相当于给目标函数增加了一项额外的约束(constrain),而且这个约束并没有体现在目标函数里,在计算过程中这样的约束是很难处理的。PPO的做法就是将这样约束融进了目标函数,其目标函数如下:
J P P O θ ′ ( θ ) = E ( s t , a t ) ~ π θ ′ [ p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) ] − β K L ( θ , θ ′ ) J_{PPO}^{\theta'}(\theta) = E_{(s_t,a_t)~\pi_{\theta'}}[ \frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}} A^{\theta'}(s_t, a_t)] - \beta KL(\theta, \theta') JPPOθ′(θ)=E(st,at)~πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)]−βKL(θ,θ′)
上面的式子我们可以理解为:训练一个累计回报期望更高但是又和 θ ′ {\theta'} θ′很像的 θ {\theta} θ。
PPO算法流程:
- 初始化一组参数 θ 0 {\theta^0} θ0
- 进行多轮迭代,每轮迭代中做以下工作:
- 使用当前参数 θ k {\theta^k} θk与环境做互动,产生 { s t , a t } \{ s_t,a_t \} { st,at},并且计算出 p θ ′ ( a t ∣ s t ) p_{\theta'(a_t|s_t)} pθ′(at∣st)和 A θ ′ ( s t , a t ) A^{\theta'}(s_t, a_t) Aθ′(st,at);
- 利用 J P P O θ k ( θ k + 1 ) J_{PPO}^{\theta^{k}}(\theta^{k+1}) JPPOθk(θk+1),求得基于当前数据 { s t , a t } \{ s_t,a_t \} { st,at}的最优参数 θ k + 1 \theta^{k+1} θk+1(这个优化过程是多次反向传播的)
上面从 θ k \theta^{k} θk到 θ k + 1 \theta^{k+1} θk+1的优化过程中,可以更新很多次也没有关系,因为我们使用了重要性采样,也对 θ \theta θ的动作空间进行了约束,这一步的目的就是尽可能的最大化目标函数。
针对上面的算法还有一个自使用KL约束的方法,叫做adaptive KL divergence,其实就是动态调整 β \beta β,如下:
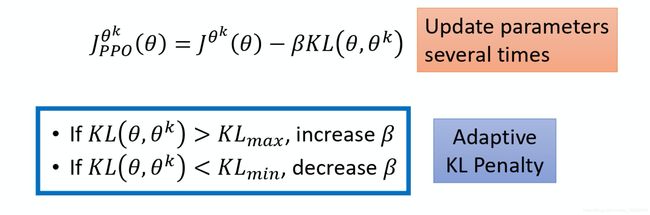
这个方法里面要设置一个我们可以接受的KL散度的上限和下限:
- 当 KL 散度的项太大,超过上限时,我们认为是我们的KL约束太弱了,才导致 θ k \theta^{k} θk和 θ k + 1 \theta^{k+1} θk+1的差异那么大,所以就把 β \beta β调大。
- 当 KL 散度的项太小,超过下限时,我们认为是我们的KL约束太强了,导致我们的训练目标变成了让 θ k + 1 \theta^{k+1} θk+1和 θ k \theta^{k} θk一样,而没有充分学习 { s t , a t } \{ s_t,a_t \} { st,at}中的知识,所以要把 β \beta β调小。
5. PPO2
PPO2也叫做PPO-Clip,该方法不采用KL散度作为约束,而是采用逻辑上合理的思路设计目标函数,其目标函数如下:
J P P O 2 θ ′ ( θ ) ≈ ∑ ( s t , a t ) min ( p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) A θ ′ ( s t , a t ) , c l i p ( p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) , 1 − ϵ , 1 + ϵ ) A θ ′ ( s t , a t ) ) \begin{aligned} J_{PPO2}^{\theta'}(\theta) \approx \sum_{(s_t, a_t)} \min(&\frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}}A^{\theta'}(s_t, a_t), \\ &clip(\frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}}, 1-\epsilon, 1+\epsilon) A^{\theta'}(s_t, a_t)) \end{aligned} JPPO2θ′(θ)≈(st,at)∑min(pθ′(at∣st)pθ(at∣st)Aθ′(st,at),clip(pθ′(at∣st)pθ(at∣st),1−ϵ,1+ϵ)Aθ′(st,at))
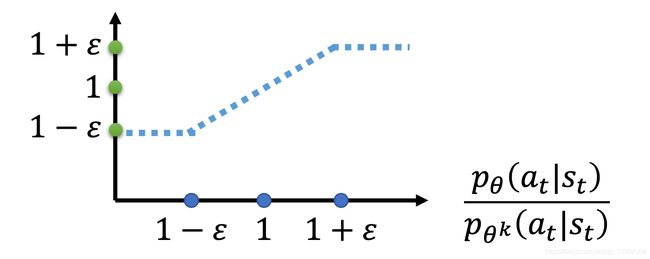
clip 函数的意思是,在括号里面有三项,分别是(变量,下限,上限),如果变量小于下限,那么就输出下限,大于上限就输出上限,如果在二者之间,就输出变量的值, c l i p ( p θ ( a t ∣ s t ) p θ ′ ( a t ∣ s t ) , 1 − ϵ , 1 + ϵ ) clip(\frac{p_{\theta(a_t|s_t)}}{p_{\theta'(a_t|s_t)}}, 1-\epsilon, 1+\epsilon) clip(pθ′(at∣st)pθ(at∣st),1−ϵ,1+ϵ)的函数图像如下。
直接分析目标函数,我们可以知道这个函数的取值逻辑如下:
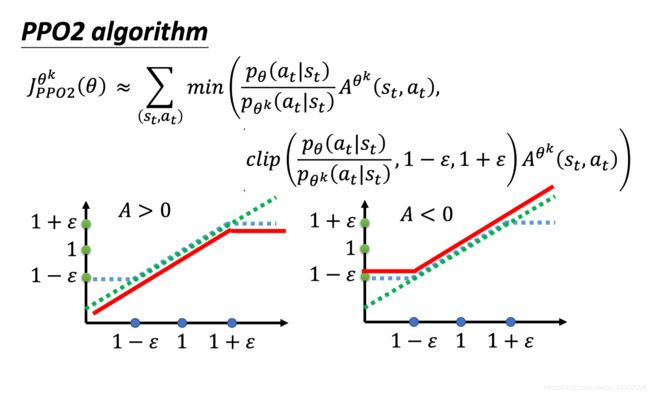
- p θ ( a t ∣ s t ) p θ k ( a t ∣ s t ) \frac{p_{\theta(a_t|s_t)}}{p_{\theta^k(a_t|s_t)}} pθk(at∣st)pθ(at∣st)是绿色的线;
- c l i p ( p θ ( a t ∣ s t ) p θ k ( a t ∣ s t ) , 1 − ϵ , 1 + ϵ ) clip(\frac{p_{\theta(a_t|s_t)}}{p_{\theta^k(a_t|s_t)}}, 1-\epsilon, 1+\epsilon) clip(pθk(at∣st)pθ(at∣st),1−ϵ,1+ϵ)是蓝色的线;
- 在绿色的线跟蓝色的线中间,我们要取一个最小的。假设前面乘上的这个项 A,它是大于 0 的话,取最小的结果,就是左侧图片中红色的这一条线。
- 同理,如果 A 小于 0 的话,取最小的以后,就得到右侧侧图片中红色的这一条线。
知道 J P P O 2 θ k ( θ ) J_{PPO2}^{\theta^k}(\theta) JPPO2θk(θ)的取值逻辑之后,我们就可以来分析将目标函数设计成这样的目的和想法。
目标函数想做的事情就是希望在提升累计期望回报的同时,保证 p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st)和 p θ k ( a t ∣ s t ) {p_{\theta^k(a_t|s_t)}} pθk(at∣st)不要差距太大,那他是如何做到的呢?
- A是比较优势,A>0表示比较优势大,我们要提升 p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st),A<0表示这个决策不好,所以我们要减少 p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st)。这里说的是不考虑重要性采样的情况。
- 当A>0时,我们要提升 p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st),可是受到重要性采样的约束,他不能和 p θ k ( a t ∣ s t ) {p_{\theta^k(a_t|s_t)}} pθk(at∣st)相差太大,所以当 p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st)大到, p θ ( a t ∣ s t ) p θ k ( a t ∣ s t ) > 1 + ϵ \frac{p_{\theta(a_t|s_t)}}{p_{\theta^k(a_t|s_t)}}>1+\epsilon pθk(at∣st)pθ(at∣st)>1+ϵ时,就不再让目标函数有benifit了,他的做法就是让 c l i p ( p θ ( a t ∣ s t ) p θ k ( a t ∣ s t ) , 1 − ϵ , 1 + ϵ ) clip(\frac{p_{\theta(a_t|s_t)}}{p_{\theta^k(a_t|s_t)}}, 1-\epsilon, 1+\epsilon) clip(pθk(at∣st)pθ(at∣st),1−ϵ,1+ϵ)这一项恒定为 1 + ϵ 1+\epsilon 1+ϵ。因为固定后,无论 p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st)变到多大,目标函数都不会有收益,自然也就不会训练到更大。
- 当A<0时,我们要减小 p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st),同样 p θ ( a t ∣ s t ) p θ k ( a t ∣ s t ) < 1 − ϵ \frac{p_{\theta(a_t|s_t)}}{p_{\theta^k(a_t|s_t)}}<1-\epsilon pθk(at∣st)pθ(at∣st)<1−ϵ时,就会停止,没有benifit, p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st)自然也就不会过小了。
有一点可以可能不清晰的是,为什么A>0时,下限不做约束,A<0时上限不做约束。原因是,如果A>0, p θ ( a t ∣ s t ) {p_{\theta(a_t|s_t)}} pθ(at∣st)一定朝着变大的方向优化,不可能变小,所以不需要约束下限;A<0时也是同理。