Learning by Playing – Solving Sparse Reward Tasks from Scratch

Learning by Playing – Solving Sparse Reward Tasks from Scratch

DeepMind 2018
原文链接
code

摘要

本文提出一种新的强化学习范式——计划辅助控制SAC-X（Scheduled Auxiliary Control）。SAC-X可以在奖励信号稀疏的情况下从头开始学习复杂的行为。为此，agent配备了一组常规的辅助任务，通过off-policy RL同时的学习。
此方法的关键思想是：主动（学习）调度并执行辅助策略，使agent能够有效的探索环境，从而使其能够胜任稀疏奖励RL。

1. Introduction

请考虑如下任务：agent学习控制机械臂打开盒子并在其中放置一个立方体。 虽然此任务的奖励定义起来简单明了（例如，使用盒子内部的简单装置（如力传感器）来检测放置的立方体），但潜在的学习问题却很难。 agent必须发现很长的“正确”动作序列，才能找到产生稀疏奖励的环境状态，即立方体在盒子内。 发现这种稀疏的奖励信号是一个非常困难的探索问题，通过随机探索获得成功的可能性极小。

过去的方法，如shaping rewards、curriculum learning、sim2real、learning from demonstrations、learning with model guidance、inverse RL都需要依赖于特定任务的先验知识。这可能会使控制策略导向依赖于先验知识的次优解。理想情况下，我们应减少应对稀疏奖励所需的特定先验任务知识。

本文介绍了一种称为调度辅助控制的新方法（SAC-X，其中X表示调度程序类型）。它基于四个主要原则：

1. 每个状态-动作对都与一个奖励向量配对，该奖励向量由（通常是稀疏的）外部提供的奖励和（通常是稀疏的）内部辅助奖励组成。
2. 每个奖励条目都有一个分配的策略——“意图（intention）”，该策略经过训练可以最大化其相应的累积奖励。
3. 有一个高层调度器，用于选择和执行单独的意图，目的是提高agent在外部任务上的性能。
4. 学习是off-policy的（与策略执行异步地进行），并且意图之间的经验可以共享-以高效的利用信息。

尽管本文中提出的方法适用于更广泛的问题，但我们将采用具有稀疏奖励的典型机器人操作任务来讨论我们的方法：堆叠各种物体和清洁桌子。

这些任务的辅助奖励是基于对agent控制自身 sensory observations 的精确掌握。被设计为易于在实际的机器人设置中实施。特别是，我们在原始感官级别上定义辅助奖励。例如是否检测到接触；或者，也可以在需要少量预先计算的较高级别上对其进行定义，例如在图像中是否有物体移动或是否有两个物体互相靠近。基于这些基本的辅助任务，agent必须有效的探索其环境，直到观测到更多外部奖励为止。

我们中仿真中演示了SAC-X在使用机器人手臂进行具有挑战性的机器人操纵任务的性能。所有任务奖励都是易于定义的稀疏奖励，并使用同一组辅助奖励函数来解决。 另外，我们证明了我们的方法是样本高效的，使我们能够从真实的机器人上从头开始学习。

3. Preliminaries

马尔可夫决策过程MDP： $\mathcal{M}$。
状态：$\mathbf{s}\in {\mathbb{R}}^S$，我们将state和observation（例如本体感受特征，物体位置或图像）互换使用，以简化表示。
动作：$\mathbf{a}\in {\mathbb{R}}^A$
状态转移概率密度 : $p({\mathbf{s}}_{t+1}|{\mathbf{s}}_t,{\mathbf{a}}_t)$
策略分布：${\pi }_{\theta }(\mathbf{a}|\mathbf{s})$
reward: $r_{\mathcal{M}}({\mathbf{s}}_t,{\mathbf{a}}_t)$
强化学习的目标是最大化折扣奖励的总和:
${\mathbb{E}}_{\pi }\left[R\left({\tau }_{0:\infty }\right)\right]={\mathbb{E}}_{\pi }[{\sum }_{t=0}^{\infty }{\gamma }^{t}r\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)|a_t\sim \pi \left(\cdot |{\mathbf{s}}_t\right),{\mathbf{s}}_{t+1}\sim p\left(\cdot |{\mathbf{s}}_t,{\mathbf{a}}_t\right),{\mathbf{s}}_0\sim p(\mathbf{s})]$
其中$p(\mathbf{s})$表示初始状态分布，${\tau }_{t:\infty }=\left\{\left({\mathbf{s}}_t,{\mathbf{a}}_t\right),\dots \right\}$ 表示从状态$t$开始的trajectory。

4. Scheduled Auxiliary Control

我们定义一个稀疏奖励问题，即找到主MDP$\mathcal{M}$的最优策略${\pi }^{\ast }$，$\mathcal{M}$的reward函数定义为：
$$r_{\mathcal{M}}(\mathbf{s},\mathbf{a})=\{\begin{array}{ll}{\delta }_{{\mathbf{s}}_g}(\mathbf{s})& \text{ if }d\left(\mathbf{s},{\mathbf{s}}_g\right)\le ϵ\\ 0& \text{ else }\end{array}（1）$$
${\mathbf{s}}_g$为目标状态，$d(\mathbf{s},{\mathbf{s}}_g)$为目标状态与当前状体$\mathbf{s}$之间的距离，可以定义为 $d(\mathbf{s},{\mathbf{s}}_g)=||\mathbf{s}-{\mathbf{s}}_g|{|}_2$。 ${\delta }_{{\mathbf{s}}_g}(\mathbf{s})$为在epsilon范围内的奖励，我们设$ϵ$很小，且${\delta }_{{\mathbf{s}}_g}(\mathbf{s})=1$。

4.1 A Hierarchical RL Approach for Learning from Sparse Rewards

我们提出一种算法，通过一组低级辅助任务来增强解决稀疏学习问题的能力。

定义辅助MDPs为 $\mathcal{A}={\mathcal{A}}_1,...,{\mathcal{A}}_k$ ，这些辅助MDPs与主任务$\mathcal{M}$共享state、observation和action空间以及transition dynamics，但是有独立的辅助奖励$r_{{\mathcal{A}}_1}(\mathbf{s},\mathbf{a}),...r_{{\mathcal{A}}_k}(\mathbf{s},\mathbf{a})$。

我们假设可以完全控制辅助奖励；即我们可以计算任何状态-动作对的辅助奖励。乍一看这个假设似乎有很大的局限性，但我们会像前面提到的那样，利用传感器获得简单的辅助奖励。

给定reward functions集，我们可以定义意图策略intention policy为${\pi }_{\theta }(\mathbf{a}|\mathbf{s},\mathcal{T})$,其奖励总和return为：
$${\mathbb{E}}_{{\pi }_{\mathbf{\theta }}(\mathbf{a}|\mathbf{s},\mathcal{T})}\left[R_{\mathcal{T}}\left({\tau }_{t:\infty }\right)\right]={\mathbb{E}}_{{\pi }_{\mathbf{\theta }}(\mathbf{a}|\mathbf{s},\mathcal{T})}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_{\mathcal{T}}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]，(2)$$
其中，$\mathcal{T}\in \mathcal{T}=\mathcal{A}\cup \{\mathcal{M}\},\text{ respectively. }$

为了根据这些定义推导出学习的目标函数，首先提醒自己我们的学习目标是：1）训练所有的辅助意图策略和主任务策略来实现他们各自的目标，2）利用所有的意图快速探索主 sparse-reward MDP $\mathcal{M}$. 为此，我们定义了一个分层目标，将策略训练分为两个部分。

learning the intentions 第一部分为所有intentions的联合策略改进目标。定义任务$\mathcal{T}$的动作-值函数$Q_{\mathcal{T}}({\mathbf{s}}_t,{\mathbf{a}}_t)$为：$$Q_{\mathcal{T}}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)=r_{\mathcal{T}}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)+\gamma {\mathbb{E}}_{{\pi }_{\mathcal{T}}}\left[R_{\mathcal{T}}\left({\tau }_{t+1:\infty }\right)\right]，（3）$$其中，${\pi }_{\mathcal{T}}$ 为 ${\pi }_{\theta }(\mathbf{a}|\mathbf{x},\mathcal{T})$ 的简写。联合策略改进目标为${\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{m}\mathbf{a}\mathbf{x}}_{\theta }\mathcal{L}(\theta )$,其中$\theta$为所有intention参数的集合。
$$\begin{array}{rl}\mathcal{L}(\mathbf{\theta })& =\mathcal{L}(\mathbf{\theta };\mathcal{M})+\sum _{k=1}^{|\mathcal{A}|}\mathcal{L}\left(\mathbf{\theta };{\mathcal{A}}_k\right)，（4）\\ \text{ with }\mathcal{L}(\mathbf{\theta };\mathcal{T})& =\sum _{\mathcal{B}\in \mathcal{T}}\underset{p(s|\mathcal{B})}{E}[Q_{\mathcal{T}}(\mathbf{s},\mathbf{a})\left|\mathbf{a}\sim {\pi }_{\mathbf{\theta }}(\cdot |\mathbf{s},\mathcal{T})\right]，（5）\end{array}$$
也就是说，我们从状态分布 $p(\mathbf{s}|\mathcal{B})$ 中的初始状态开始，优化每个intention，以为其任务选择最佳动作。$p(\mathbf{s}|\mathcal{B})$ 通过遵循其他策略${\pi }_{\theta }(\mathbf{a}|\mathbf{s},\mathcal{B})$ 且$\mathcal{B}\in \mathcal{J}=\mathcal{A}\cup \{\mathcal{M}\}$。

我们注意到，这与多任务RL公式相比有微妙但重要的变化。 通过从各自可能的任务的状态分布中抽样得到的状态训练各自的策略，我们获得的策略是“兼容的”，从某种意义上说，他们可以解决各自的任务而不受先前的intention policy结束时系统所处的状态的影响。这对于要安全的结合所学的intention polixy来说是至关重要的。

Learning the scheduler 分层目标的第二部分是学习一个调度器scheduler来sequences（排序） intention-policies。考虑如下设定：用$\xi$表示scheduler可以在tasks之间切换的时间段,进一步用$H$表示episode内可能的任务切换（包括初始intention选择）的总数，用${\mathcal{T}}_{0:H-1}=\left\{{\mathcal{T}}_0,\dots ,{\mathcal{T}}_{H-1}\right\}$表示一个episode中的$H$个调度选择。我们可以定义主任务的return为
$$\begin{array}{c}{R}_{\mathcal{M}}\left({\mathcal{T}}_{0:H-1}\right)={\sum }_{h=0}^H{\sum }_{t=h\xi }^{(h+1)\xi -1}{\gamma }^t{r}_{\mathcal{M}}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)，（6）\\ \text{ where }{\mathbf{a}}_t\sim {\pi }_{\mathbf{\theta }}\left(\cdot |{\mathbf{s}}_t,{\mathcal{T}}_h\right)\end{array}$$ 定义scheduling policy为$P_s(\mathcal{T}|{\mathcal{T}}_{0:h-1})$，当行为依据scheduler时，动作${\mathbf{a}}_t$的概率为$${\pi }_{\mathcal{S}}\left({\mathbf{a}}_t|{\mathbf{s}}_t,{\mathcal{T}}_{0:h-1}\right)=\sum _{\mathcal{T}}{\pi }_{\mathbf{\theta }}\left({\mathbf{a}}_t|{\mathbf{s}}_t,\mathcal{T}\right)P_{\mathcal{S}}\left(\mathcal{T}|{\mathcal{T}}_{0:h-1}\right)$$
从中我们可以分两步进行采样（如式（6））：首先每$\xi$步选择一个子任务，然后从相应的intention中抽取一个action；我们注意到选择的子任务可以是辅助任务也可以是主任务。 结合这两个定义，学习scheduler $\mathcal{S}$的目标$\mathcal{L}(\mathcal{S})$为找到${\mathbf{a}\mathbf{r}\mathbf{g}\mathbf{m}\mathbf{a}\mathbf{x}}_{\mathcal{S}}\mathcal{L}(\mathcal{S})$。
$$\mathcal{L}(\mathcal{S})={\mathbb{E}}_{P_{\mathcal{S}}}[R_{\mathcal{M}}\left({\mathcal{T}}_{0:H-1}\right)\left|{\mathcal{T}}_h\sim P_{\mathcal{S}}\left(\mathcal{T}|{\mathcal{T}}_{0:h-1}\right)\right].（8）$$
请注意，为了优化scheduler，我们考虑固定式(8)中各自的intentions，即没有对参数$\theta$进行优化。因为否则我们将无法保证保留各个intentions（首先我们需要intentions进行有效的探索）。我们还注意到，如上定义的scheduling策略忽略了对状态${\mathbf{s}}_{h\xi }$的依赖， in which a task is scheduled (i.e. $P_{\mathcal{S}}$ uses a partially observed state)。除了这个学到的scheduler，我们还实验了一种在整个episode中随机调度intentions的版本，用SAC-U表示。注意，这个策略并不像它最初出现时那样简单：由于我们允许中一个episode中调度多个intentions，因此他们会自然的胃彼此提供curriculum训练数据。例如，一个成功的“移动物体”intention会将机器人手臂停留在靠近该物体的位置，会使得“抬升”intention很容易发现奖励。

上面描述的问题公式与其他几种多任务RL公式相似。 特别要强调的是，它可以解释为IUA和UN-REAL目标对随机连续控制的概括-结合episode中活动的辅助任务执行和（可能学习的）调度。 也可以将其理解为Hindsight Experience Replay的分层扩展，在该扩展中，agent根据一组固定的，基于语义的辅助任务进行操作-而不是遵循随机目标-并对任务选择进行优化。

4.2 policy improvement

为了优化式(5)的目标，我们采用基于梯度的方法。首先我们要注意的是，对于每个intention$\pi (\mathbf{a}|\mathbf{s},\mathcal{T})$,必须要off-policy处理，因为我们希望每个策略都可以从其他所有策略生成的数据中学习。为此，我们假设可以得到状态-动作值的参数化估计值${\hat{Q}}_{\mathcal{T}}^{\pi }(\mathbf{s},\mathbf{a};\varphi )$，即，${\hat{Q}}_{\mathcal{T}}^{\pi }(\mathbf{s},\mathbf{a};\varphi )\approx Q_{\mathcal{T}}^{\pi }(\mathbf{s},\mathbf{a})$。利用这个估计值以及包含从策略收集的trajecties $\tau$ 的replay buffer $B$，可以采用下列梯度式来更新策略参数 $\theta$ ：
其中 ${\mathbb{E}}_{{\mathbf{\pi }}_{\mathbf{\theta }}\left(\cdot |{\mathbf{s}}_t,\mathcal{T}\right)}\left[\log {\pi }_{\mathbf{\theta }}\left(\mathbf{a}|{\mathbf{s}}_t,\mathcal{T}\right)\right]$ 对应于一个附加的（每个时间步）熵正则化项（具有加权参数$\alpha$）。 可以通过重新参数化技巧计算此梯度，因为策略的采样过程时可微分的（例如此处使用的高斯策略）。

与intention策略不同，scheduler必须快速适应输入实验数据流的变化，因为intention会随着时间变化，因此在学习过程中任何intention触发主任务reward的可能性都存在很大差异。为解决这一问题，我们为scheduler选择了一个简单的参数形式：假设一组离散的任务$\mathcal{J}$，首先有如下解决方案：
$$P_{\mathcal{S}}=\arg \underset{P_{\mathcal{S}}}{\max }\mathcal{L}(\mathcal{S})，（10）$$
式（8）可以采用Boltzmann分布近似：
其中温度参数$\eta$ 决定schedule的贪婪程度。因此 ${\lim }_{\eta \to 0}{P}_{\mathcal{S}}\left(\mathcal{T}|{\mathcal{T}}_{1:h-1};\eta \right)$ 对应于任何调度点的最优策略(式(10)的解)。确切地说，玻尔兹曼策略与最大化$\mathcal{L}(\mathcal{S})$以及scheduler上的附加熵正则化函数相对应。

这个分布可以用schedule returns近似表示 $Q\left({\mathcal{T}}_{1:h-1},{\mathcal{T}}_h\right)\approx {\mathbb{E}}_{P_{\mathcal{S}}}\left[R_{\mathcal{M}}\left({\mathcal{T}}_{h:H}\right)|{\mathcal{T}}_{1:h-1}\right]$ 。 对于finite，少量的小任务（如本文所述），$Q\left({\mathcal{T}}_{1:h-1},{\mathcal{T}}_h\right)$ 可以用表格的形式表示。具体来说，我们使用最后的M=50个运行trajectories形成蒙特卡洛估计：$$Q\left({\mathcal{T}}_{0:h-1},{\mathcal{T}}_h\right)=\frac{1}{M}\sum _{i=1}^M{R}_{\mathcal{M}}^{\tau }\left({\mathcal{T}}_{h:H}\right)，（12）$$ 其中$R_{\mathcal{M}}^{\tau }\left({\mathcal{T}}_{h:H}\right)$ 是沿着trajectory $\tau$ 的累积折扣return（按式(6)计算，但具有固定状态和动作选择）。

4.3 policy Evaluation

我们使用Retrace对所有intentions进行off-policy评估。 具体来说，我们通过最小化下列loss，来训练参数化Q函数(神经网络)${\hat{Q}}_{\mathcal{T}}^{\pi }(\mathbf{s},\mathbf{a};\varphi )$，loss根据replay $B$ 的数据来定义：
$$\begin{array}{l}{\min }_{\varphi }L(\varphi )={\mathbb{E}}_{(\tau ,b,\mathcal{B})\sim B}\left[{\left({\hat{Q}}_{\mathcal{T}}^{\pi }(\mathbf{s},\mathbf{a};\varphi )-Q^{\text{ret }}\right)}^2\right],\text{ with }\\ Q^{\text{ret }}={\sum }_{j=i}^{\infty }\left({\gamma }^{j-i}{\prod }_{k=i}^j{c}_k\right)\left[r_{\mathcal{T}}\left(s_j,a_j\right)+{\delta }_Q\left({\mathbf{s}}_i,{\mathbf{s}}_j\right)\right]\\ {\delta }_Q\left({\mathbf{s}}_i,{\mathbf{s}}_j\right)=\gamma {\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}(\mathbf{a}|\mathbf{s},\mathcal{T})}\left[Q_{\mathcal{T}}^{\pi }\left({\mathbf{s}}_i,\cdot ;{\varphi }^{\prime }\right)\right]-Q_{\mathcal{T}}^{\pi }\left({\mathbf{s}}_j,{\mathbf{a}}_j;{\varphi }^{\prime }\right)\\ c_k=\min \left(1,\frac{{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_k|{\mathbf{s}}_k,\mathcal{T}\right)}{b\left({\mathbf{a}}_k|{\mathbf{s}}_k,\mathcal{B}\right)}\right)\end{array}，（13）$$ 其中 $\tau$ 表示从replay buffer 采样的trajectory(包含动作选择和奖励)，$b$表示生成数据的行为策略，$\mathcal{B}$表示行为策略试图完成的任务。我们再次强调 $b$并不旨在完成任务 $\mathcal{T}$ for which ${\hat{Q}}_{\mathcal{T}}$ 应该预测动作值。重要性权重$c_k$对在行为策略(概率为$\pi$)下选择的action进行加权。${\varphi }^{\prime }$和${\theta }^{\prime }$为目标策略和Q-networks的餐素，与当前参数$\varphi$、$\theta$定期交换。这是Deep-RL算法中提高学习稳定性的常用方法。

5. 实验

为了对我们的方法进行基准测试，我们用Kinova Jaco机械臂在仿真和实物上进行了实验。

5.1 实验设置

在所有实验中都选择了辅助任务来为agent提供（有关其对自身感觉空间探索程度的）信息。 从它们在任务之间transfer的意义上来说，它们是易于计算且通用。 它们是在所有可用的传感器模式上定义的。 例如，对于本体感受proprioception，我们选择最大化/最小化关节角度，对于接触传感器，我们定义了激活/禁用手指触觉或力-力矩矩传感器的任务。 在图像空间中，我们在object级别上定义了辅助任务（即“移动红色物体”或“将红色物体放到相机平面中的绿色物体旁边”）。 所有这些叙述都可以轻松计算并映射到稀疏奖励信号（如公式（1）中所示）。下文中列出了完整的奖励清单。

我们介绍了SAC-X的学习结果（其中X表示scheduler的类型），其中包含第4.1节中描述的两个scheduler类型：顺序统一的scheduler(SAC-U)和学到的scheduler(SAC-Q)。 在消融(ablation)研究中，我们还设置的non-scheduling版本，在该版本中，我们严格遵循了优化外部奖励的政策。 由于此过程与IU agent的过程类似，我们在下文中以“ IUA”表示该变体。 我们还与强有力的off-policy学习基线DDPG做了比较。

所有仿真实验均以50 ms时间步长使用原始关节速度（9 DOF）作为控制信号。一个episodes总共有360步，每$\xi =180$步scheduler做一次选择，即每个episode做两次选择。我们注意到，在我们的设置中，一个episode中有两个intention切换就足够了，因为intentions形成了层次结构——因此，一旦获得了足够多的学习“lift”的数据，在一个scheduling cycle 中一个“lift” intention就可以实现“touch”和“move”两个intention。observations包含机械臂的propriocetive信息(关节角，关节速度)、来自腕部的力-力矩传感器和手指触觉传感器的传感器信息和相机图像信息。我们提供了从原始像素和提取的特征（即场景中物体的位姿和速度）中学习的结果，有关策略结构的详细信息，请参考补充材料。使用5个不同的随机种子重复所有实验；学习曲线报告了运行过程中的中位数性能（阴影区域分别表示5％和95％）。

为了加快实验速度，所有仿真实验的结果都是在off-policy学习设置中获得的，该策略中的数据是由多个agent（36个actor）收集的，这些agent将收集的经验池发送给36个learners。 此设置在补充材料中有更详细的说明。 尽管这是data-efficiency的一个折衷方案——要权衡时间——但我们的真实实验表明，SAC-X可以实现非常高的数据效率，在该实验中，近用了一个机器人来采集数据。

5.2 Stacking Two Blocks

物块堆叠任务：将一个物块堆叠在另一个稍大的物块之上。 这是一项具有挑战性的机器人操作任务，因为它要求agent掌握这些核心能力：抓住放置在工作区中任意位置的第一个物块，将其提升到一定高度，将其精确地放置在第二个物块的顶部。 另外，agent必须找到两个块的稳定配置。 预期的行为在图4的底部图像序列中显示。我们给予成功的堆叠稀疏的奖励：较小的物块仅与场景中的其他物块接触，而不与机器人或地面接触； 否则，奖励为零。 除此主要任务奖励外，agent还可以访问补充材料中定义的标准辅助奖励集。

图1显示了SAC-X与几个baselines 之间在平均堆叠奖励方面的比较。 如图所示，所有种子的SAC-U（统一调度）和SAC-Q都能可靠地学习任务。 每个actor大约收集了5000个 episodes后，SAC-U实现了良好的表现，而SAC-Q的速度更快，并且最终性能有所提高-这要归功于其学到的scheduler。 为了证明我们的方法足够强大，可以从原始图像中学习策略和动作值函数，我们用两个相机的图像信息（经CNN处理然后与 proprioceptive sensor 信息连接融合）替换了物块的位置信息，执行相同的叠加实验。 该实验的结果表明，虽然从像素（SAC-Q(pixels)）学习比从特征学习要慢，但可以学习到相同的整体行为。

图1. 将第一个物块堆叠在第二个物块上的外部任务的累积奖励。 SAC-U和SAC-Q都能可靠地学习任务。 使用DDPG的参考实验完全失败（实线）。 IUA方法学习速度较慢且可靠性较低。 注意，所有结果都是通过36个actors和learners获得的。

在没有scheduling的情况下，即当agent遵循由外部奖励(IUA)引导的行为策略时，IUA agent会在实验的前半部分获得偶尔的成功， followed by late learning of the task。由于策略网络中的共享层将行为偏向于触摸/提起砖块，因此推测仍然是可能学会的（一旦观察到，Retrace会沿轨迹迅速传播奖励）。但是学习过程的可变性要高得多，学习速度要慢得多。最终，DDPG无法完成此任务。其原因是，纯粹的随机探索很难观察到堆叠奖励，因此DDPG无法收集学习所需的数据。这两个结果都支持一个核心猜想：调度和执行辅助 intentions 可以在稀疏的奖励设置中实现可靠而成功的学习。图2 给出了学习行为的一些见解，绘制了学习intentions的子集（有关所有结果，请参见补充资料）。agent首先学会接触（TOUCH）或远离物块（NOTOUCH），然后学会移动物块并最终堆叠起来。

图2. 在SAC-Q方法中我们使用的13个辅助intentions子集的学习时间。 红色代表reward。首先agent接触并移动物体来学习与物体进行交互，然后可以学习更复杂的intention，直到最终学会堆叠。

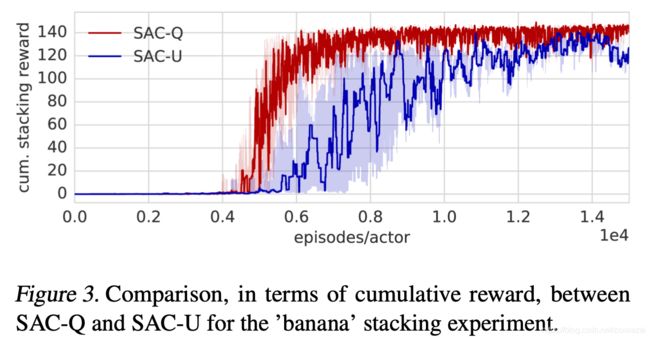
5.3 Stacking a ’Banana’ on Top of a Block

与简单的方块相比，使用不那么规则的物体在抓取和堆叠方面都带来了其他挑战：某些物体的形状仅允许特定的抓握姿态，或者很难以稳定的配置堆叠。 因此，我们执行了第二个实验，将香蕉形物体放置在方块的顶部。 对于依赖shaping rewards的方法，这将需要仔细调整shaping。 而对于SAC-X方法，我们则可使用同一组辅助任务。

图3描述了该实验的结果。 SAC-U和SAC-Q均可解决该任务。 但是，在这种情况下，专注于解决外部任务的learning scheduler的优势变得更加明显。 对此的一种解释是，堆叠香蕉确实需要对堆叠策略进行仔细的微调-学习的scheduler 自然会将重点放在该策略上。

5.4 Stacking Blocks Both Ways

然后我们拓展了堆叠任务，要求agent学习两任务：将红色方块堆叠到大的绿色方块上（图4，1在2上），反过来将绿色方块放到红色上（图4，2张1上），这是一项艰难的堆叠任务。这是一个agent学习多个外部任务的示例。 为了应付多个外部任务，我们学习了多个schedulers（每个任务一个），并在它们之间随机选择（假设外部任务具有相同的重要性）。

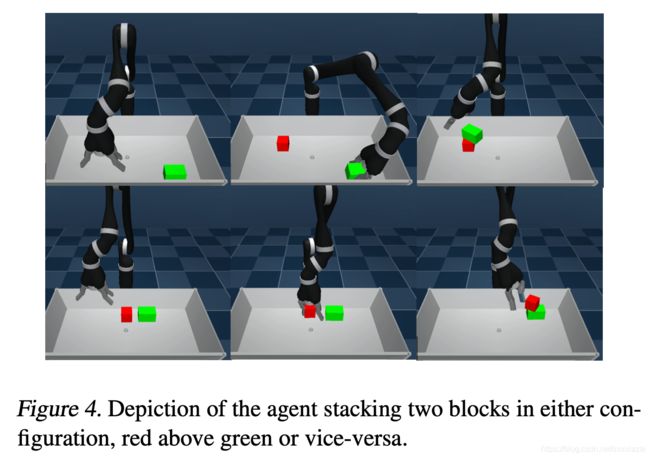
SAC-U和SAC-Q都能从pure rewards完成外部任务（图5）。从图中还可以明显看出，SAC-X agent 有效地利用了其replay buffer：最初的堆叠实验(5.2节)每个actor需要5000个episodes，而SAC-X 每个actor仅需要2500个附加episodes来学习附加任务。除了这种定量评估外，我们注意到learned agent的观测行为表现出了intuitive的策略来应对复杂的情况。例如，如果agent是在方块1已经堆叠在方块2上的情况下开始的，那么它已经学会了先将方块1放在桌子上，然后将方块2堆叠到方块1上面——这是在同一个policy中发生的。

5.5. The ’clean-up’ Task

清理任务（图6）是一个执行一系列特定动作才能解决的一个任务示例。除了上一实验中两个大小不同的方块外，我们还在场景中添加了一个新对象：一个可以打开盖子的盒子。
我们依赖于堆叠方块实验中相同的辅助任务，给每个与盒子相关的方块添加了一个额外的稀疏辅助intention：“将方块带到盒子的上方靠近盒子的位置”。与前面的实验不同，我们现在有4个稀疏的外部任务和相应的intention策略：
1）打开盒子（图中的 OPENBOX ）
2）将方块1放入盒子（ INBOX(1) ）
3）将放块2放入盒子（ INBOX(2) ）
4）将所有的方块放入盒子（INBOX_ALL）
总共有15个辅助任务和4个外部任务，这是本文最复杂的一个方案。图7展示了SAC-X和baselines对此任务的比较。值得注意的是，即使只有将方块放到正确的位置才能观察到将方块放入盒子的reward，SAC-Q仍然学会了所有的外部任务（图8），并且辅助任务可靠的执行并能够插入到intention策略之间。所有的baselines在此设置中均失败了，这表明SAC-X是sparse reward RL向前迈出的重要一步。

5.6 Learning from Scratch on the Real Robot

为了在真实的机器人上学习，我们考虑两个任务：拿起(lift)方块和bring任务。 我们首先用仿真实验（采用一个实时运行的actor学习）验证两个任务的可行性。使用SAC-X，可以用9 DOF关节速度控制从纯奖励中成功学习这两项任务。 但是，在真实机器人上的学习需要在真实机器人上进行几天不间断的实验。 因此，出于实际可行性，我们进行了以下调整：我们使用笛卡尔控制器进行基于速度的机械手位置控制，再加上一个用于控制两个手指的控制动作，从而产生4维连续控制矢量。 请注意，提供给控制器的本体感受proprioceptive信息仍由关节位置和速度组成。

在lift实验中，定义了三个辅助奖励（机器人闭合手指，张开手指和靠近方块的奖励）。 如图9（顶部）所示的学习曲线表明，使用单个机器人手臂，SAC-Q在大约1200个episodes后成功学习会了拿起方块，在真实机器人上需要大约10个小时的学习时间。 在真实的机器人上进行了约50次测试，agent可以100％成功地完成lift任务。

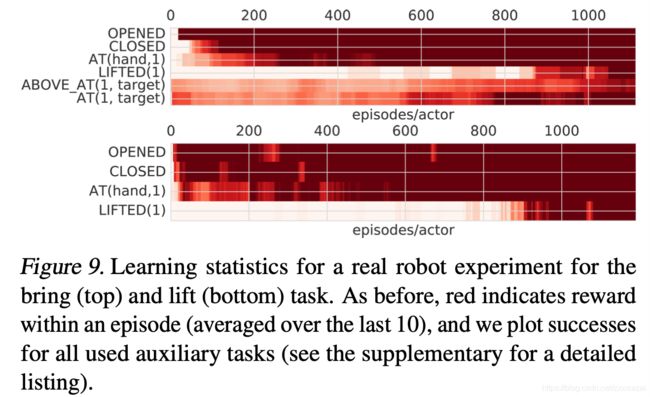
在更具挑战性的设置中，我们训练了SAC-Q将方块放置到指定位置；增加以奖励agent到达所述位置的附加任务。学习又成功了，agent显示了鲁棒的、非凡的控制行为：所产生的策略开发出了多种技术来完成任务，包括用一根手指推或拉方块以及将方块提起并携带到指定位置。此外，agent还学会了纠正未准确放置的物体的位置，还学会了完成任务后将手抓移开。这种reactive的、丰富的控制行为可以归因于我们方法的闭环形式。

6. 结论

本文介绍了SAC-X，该方法可同步学习一组辅助任务的intention策略，并主动调度并执行这些策略以探索其 observation 空间-寻找外部定义的目标任务的稀疏奖励。 利用简单的辅助任务，SAC-X可以从以“纯粹”、稀疏方式（仅指定最终目标，而不指定解决方案的路径）定义的奖励中学习复杂的目标任务。我们在仿真中用几个具有挑战性的机器人任务，在真实机器人上用一组简单稀疏的辅助任务演示了SAC-X的强大。learned intentions具有更高的反应性（reactive）、可靠性，并且表现出丰富而鲁棒的行为。我们认为这是朝着将RL应用于现实世界的目标迈出的重要一步。

我们使用一组通用的简单稀疏辅助任务和一个真实的机器人，演示了SAC-X在模拟中的几个具有挑战性的机器人任务上的强大功能。 所学的意图是高度反应性的，可靠的，并且表现出丰富而强大的行为。 我们认为这是朝着将RL应用于现实世界的目标迈出的重要一步。