第六届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第六届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第一题 积分之迷（15分）

小明开了个网上商店，卖风铃。共有3个品牌：A，B，C。

为了促销，每件商品都会返固定的积分。

小明开业第一天收到了三笔订单：

第一笔：3个A + 7个B + 1个C，共返积分：315

第二笔：4个A + 10个B + 1个C，共返积分：420

第三笔：A + B + C，共返积分…

你能算出第三笔订单需要返积分多少吗？

请提交该整数，不要填写任何多余的内容。

• 答案：105

思路：暴力枚举

1. 解方程不可取
2. 暴力枚举复杂度不高，可以使用，编写代码运行即可
3. 优化：最大积分420，A的范围不大于110，B的范围不大于50，C的范围不大于420

代码实现

#include
#include

using namespace std;

int main(){
     
	for(int i=0;i<110;i++){
     
		for(int j=0;j<50;j++){
     
			for(int k=0;k<420;k++){
     
				if(3*i+7*j+k==315 && 4*i+10*j+k==420)
					cout<<i+j+k<<endl;
			}
		}
	}
}

• 运行结果截图

• 结果说明：多个结果，都是105，说明满足这两个方程的A、B、C一定满足A+B+C=105

第二题 完美正方形（35分）

如果一些边长互不相同的正方形，可以恰好拼出一个更大的正方形，则称其为完美正方形。

历史上，人们花了很久才找到了若干完美正方形。比如：如下边长的22个正方形

2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60

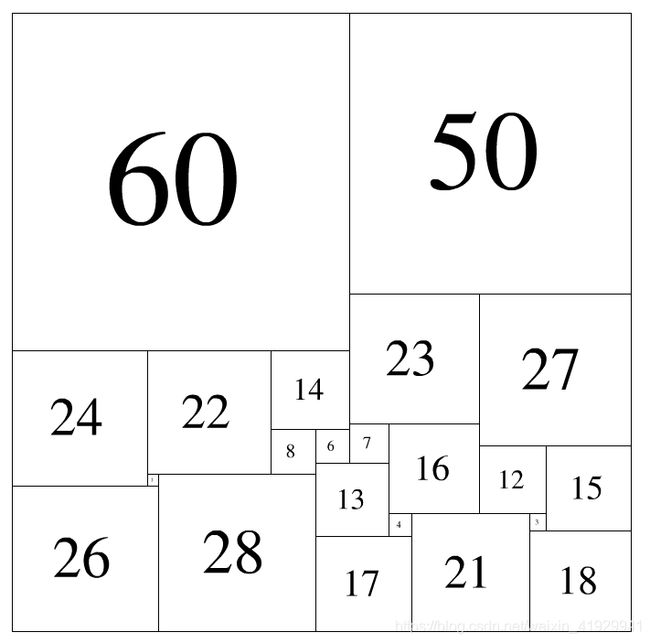
如【图1.png】那样组合，就是一种解法。此时，

紧贴上边沿的是：60 50

紧贴下边沿的是：26 28 17 21 18

22阶完美正方形一共有8种。下面的组合是另一种：

2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61

如果告诉你该方案紧贴着上边沿的是从左到右依次为：47 46 61，

你能计算出紧贴着下边沿的是哪几个正方形吗？

请提交紧贴着下边沿的正方形的边长，从左到右，用空格分开。

不要填写任何多余的内容或说明文字。

• 答案：50 33 30 41

思路：深度优先遍历（DFS）

1. 除了已经摆好的3个正方形，其余19个正方形尝试所有放法
2. 47+46+61=154，即该最终拼成的正方形边长是154
3. 申请154行154列的2维数组，对已经被摆放好的位置数组值置为1，否则置为0
4. 19层遍历，每层遍历边长为154的正方形，发现第一个没有摆放的格子时尝试摆放小正方形，如果有一个小正方形能放下，进入下一层遍历，直到第19层能放下最后一个小正方形时返回true表示摆放完成，否则返回false表示该摆放方案是失败的
5. 将最后几个边长之和为154的正方形边长依次输出（用空格分割）

代码实现

#include
#include
#define N 154
#define NUM 19
using namespace std;

int map[N][N];
int square[NUM]={
     2,5,9,11,16,17,19,21,22,24,26,30,31,33,35,36,41,50,52};
bool flag[NUM];
int record[22];

bool fill(int x,int y,int n){
     
	/*在点（x，y）处放置边长为n的小正方形，如果放置成功则返回true，否则返回false*/
	//检测在（x,y)位置能否放置边长为n的正方形 
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			if(x+i>=N||y+j>=N||map[x+i][y+j]!=0) return false;
	//在（x,y)位置放置边长为n的正方形
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			map[x+i][y+j]=n;
	return true; 
}

void cancel(int x,int y,int n){
     
	/*撤销在点（x，y）处放置边长为n的小正方形*/
	for(int i=0;i<n;i++)
		for(int j=0;j<n;j++)
			map[x+i][y+j]=0;
}

bool dp(int n){
     
	int x,y;
	bool sign=false;
	//按从左到右，从上到下的顺序找到最先出现的未被填放的位置 
	for(x=0;x<N;x++){
     
		for(y=0;y<N;y++){
     
			if(map[x][y]==0){
     
				sign=true;
				break;
			}
		}
		if(sign) break;
	}
	//全部被填满了，返回true 
	if(!sign) return true;
	for(int i=0;i<NUM;i++){
     
		if(!flag[i] && fill(x,y,square[i])){
     
			flag[i]=true;
			record[n]=square[i];
			if(dp(n+1)) return true;
			cancel(x,y,square[i]);
			flag[i]=false;
		}
	}
	return false;
}

int main(){
     
	//初始化大正方形 
	for(int i=0;i<N;i++)
		for(int j=0;j<N;j++)
			map[i][j]=0;
	//初始化小正方形使用情况 
	for(int i=0;i<NUM;i++)
		flag[i]=false;
	//放置最上边三个正方形 
	fill(0,0,47);
	fill(0,47,46);
	fill(0,93,61);
	record[0]=47;
	record[1]=46;
	record[2]=61;
	dp(3);
	cout<<"最终排列方式："<<endl;
	for(int i=0;i<22;i++){
     
		cout<<record[i]<<" ";
	}
	cout<<endl<<"最下面一排的正方形边长是：";
	int number = map[N-1][0];
	cout<<number<<" ";
	for(int i=1;i<N;i++){
     
		if(number!=map[N-1][i]) cout<<map[N-1][i]<<" ";
		number = map[N-1][i];
	}
}

• 运行结果截图

第三题 关联账户（25分）

为增大反腐力度，某地警方专门支队，对若干银行账户展开调查。

如果两个账户间发生过转账，则认为有关联。如果a,b间有关联, b,c间有关联，则认为a,c间也有关联。

对于调查范围内的n个账户（编号0到n-1），警方已知道m条因转账引起的直接关联。

现在希望知道任意给定的两个账户，求出它们间是否有关联。有关联的输出1，没有关联输出0

小明给出了如下的解决方案：

#include 
#define N 100

int connected(int* m, int p, int q)
{
     
	return m[p]==m[q]? 1 : 0;
}

void link(int* m, int p, int q)
{
     
	int i;
	if(connected(m,p,q)) return;
	int pID = m[p];
	int qID = m[q];
	for(i=0; i<N; i++) _____________________________________;  //填空位置
}

int main()
{
     
	int m[N];
	int i;
	for(i=0; i<N; i++) m[i] = i; //初始状态，每个节点自成一个连通域
	link(m,0,1); //添加两个账户间的转账关联
	link(m,1,2); 
	link(m,3,4); 
	link(m,5,6); 
	link(m,6,7); 
	link(m,8,9); 
	link(m,3,7); 
    
    printf("%d ", connected(m,4,7));
	printf("%d ", connected(m,4,5));
	printf("%d ", connected(m,7,9));
	printf("%d ", connected(m,9,2));
	return 0;
} 

请分析源代码，并提交划线部分缺少的代码。不要填写已有代码或任何多余内容。

• 答案：if(pID==m[i]) m[i]=qID

思路：分析连通图

1. int connected(int* m, int p, int q)用于判断关联
2. void link(int* m, int p, int q) 用于建立联系，即相当于将两个连通图联通成一个联通图
3. 填空位置就是将原本m[p]域内的所有节点迁移到m[q]域内

第四题 密文搜索（47分）

福尔摩斯从X星收到一份资料，全部是小写字母组成。
他的助手提供了另一份资料：许多长度为8的密码列表。
福尔摩斯发现，这些密码是被打乱后隐藏在先前那份资料中的。

请你编写一个程序，从第一份资料中搜索可能隐藏密码的位置。要考虑密码的所有排列可能性。

数据格式：

输入第一行：一个字符串s，全部由小写字母组成，长度小于1024*1024
紧接着一行是一个整数n,表示以下有n行密码，1<=n<=1000
紧接着是n行字符串，都是小写字母组成，长度都为8

要求输出：
一个整数, 表示每行密码的所有排列在s中匹配次数的总和。

例如：
用户输入：
aaaabbbbaabbcccc
2
aaaabbbb
abcabccc

则程序应该输出：
4

这是因为：第一个密码匹配了3次，第二个密码匹配了1次，一共4次。

资源约定：
峰值内存消耗 < 512M
CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

思路：子串含字母个数比较

1. 预处理长字符串：将长度为n的字符串变成一张count[n-7] [26]的二维表，这个二维表的第i行存储第i到i+7的子串含的各个字符个数
2. 每个密码都和count的所有行进行对比，如果和该行对比成功（则该子串必有一个排序可与该密码相同），计数器加1，直到匹配完所有行就完成了一个密码的匹配了
3. 一次匹配所有密码，将所有匹配数累加得到答案

代码实现

#include
#include
using namespace std;

//扫描数组s，每8个连续子串记录其包含的字符个数 
void scan(int **count,int len,char s[]){
     
	for(int i=0;i<len;i++){
     
		for(int j=0;j<8;j++){
     
			count[i][s[i+j]-'a']++;
		}
	} 
}

//比较密码是与长串多少个匹配位置 
int comp(int cmp[],int **count,int len){
     
	bool flag;
	int ans=0;
	for(int i=0;i<len;i++){
     
		flag=true;
		for(int j=0;j<26;j++){
     
			if(count[i][j]!=cmp[j]){
     
				flag=false;
				break;
			}
		}
		if(flag) ans++;
	}
	return ans;
}

int main(){
     
	char s[1024*1024];
	cin>>s;
	int n;
	//求字符串长度 
	for(n=0;s[n]!='\0';n++);
	int len=n-7;
	int **count = new int*[len];
	for(int i=0;i<len;i++) count[i]=new int[26];
	//初始化记录数组 
	for(int i=0;i<len;i++)
		for(int j=0;j<26;j++)
			count[i][j]=0;
	scan(count,len,s);
	cin>>n;
	char c[9];
	int ans=0;
	int cmp[26];
	for(int i=0;i<n;i++){
     
		cin>>c;
		for(int j=0;j<26;j++) cmp[j]=0; 
		for(int j=0;j<8;j++) cmp[c[j]-'a']++;
		ans+=comp(cmp,count,len);
		//cout<
	}
	cout<<ans;
	for(int i=0;i<len;i++) delete count[i];
	delete count;
	return 0;
}

• 运行结果

第五题 居民集会（79分）

蓝桥村的居民都生活在一条公路的边上，公路的长度为L，每户家庭的位置都用这户家庭到公路的起点的距离来计算，第i户家庭距起点的距离为di。

每年，蓝桥村都要举行一次集会。今年，由于村里的人口太多，村委会决定要在4个地方举行集会，其中3个位于公路中间，1个位最公路的终点。

已知每户家庭都会向着远离公路起点的方向去参加集会，参加集会的路程开销为家庭内的人数ti与距离的乘积。

给定每户家庭的位置di和人数ti，请为村委会寻找最好的集会举办地：p1, p2, p3, p4 (p1<=p2<=p3<=p4=L),使得村内所有人的路程开销和最小。

【输入格式】
输入的第一行包含两个整数n, L，分别表示蓝桥村的家庭数和公路长度。
接下来n行，每行两个整数di, ti，分别表示第i户家庭距离公路起点的距离和家庭中的人数。

【输出格式】
输出一行，包含一个整数，表示村内所有人路程的开销和。
【样例输入】
6 10
1 3
2 2
4 5
5 20
6 5
8 7
【样例输出】
18
【样例说明】
在距起点2, 5, 8, 10这4个地方集会，6个家庭需要的走的距离分别为1, 0, 1, 0, 2, 0，总的路程开销为13+02+15+020+25+07=18。

【数据规模与约定】
对于10%的评测数据，1<=n<=300。
对于30%的评测数据，1<=n<=2000，1<=L<=10000，0<=di<=L，di<=di+1，0<=ti<=20。
对于100%的评测数据，1<=n<=100000，1<=L<=1000000，0<=di<=L，di<=di+1，0<=ti<=1000000。

资源约定：
峰值内存消耗 < 512M
CPU消耗 < 5000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

思路：暴力枚举

1.枚举p1、p2、p3的位置
2.计算每种情况所有家庭开销和并保存最小值
3.输出最小值
优化1：枚举的时候枚举每户的位置可以减少枚举次数
优化2：每次循环就取这个循环分割出的区间的家庭到集会的距离进行计算可以减少计算次数

代码实现

#include
#include
using namespace std;

//计算路程开销 
long long spend(int l,int r,int *d,int *t){
     
	long long count=0;
	for(int i=l+1;i<=r;i++){
     
		count+=(d[r]-d[i])*t[i];
	}
	return count;
} 

int main(){
     
	int n,L,p1,p2,p3,d1,d2,d3;
	long long min=1000000000000,temp;
	cin>>n>>L;
	int d[n+1],t[n];
	for(int i=0;i<n;i++) cin>>d[i]>>t[i];
	d[n]=L;		//最后一个位置是终点方便计算 
	if(n<4){
     	//少于4个家庭一定是0（就每个家庭的位置作为集会点） 
		cout<<0;
		return 0;
	}
	//三重循环枚举集会地点 
	for(int i=0;i<n-2;i++){
     
		d1=spend(-1,i,d,t);
		for(int j=i+1;j<n-1;j++){
     
			d2=spend(i,j,d,t);
			for(int k=j+1;k<n;k++){
     
				if(d[k]==L) continue;
				d3=spend(j,k,d,t);
				temp=d1+d2+d3+spend(k,n,d,t);
				if(temp<min){
     
					min=temp;
					p1=d[i];
					p2=d[j];
					p3=d[k];
				}
			}
		}
	}
	cout<<min<<endl;
	cout<<p1<<" "<<p2<<" "<<p3;
	return 0;
}

第六题 模型染色（99分）

在电影《超能陆战队》中，小宏可以使用他的微型机器人组合成各种各样的形状。
现在他用他的微型机器人拼成了一个大玩具给小朋友们玩。为了更加美观，他决定给玩具染色。

小宏的玩具由n个球型的端点和m段连接这些端点之间的边组成。下图给出了一个由5个球型端点和4条边组成的玩具，看上去很像一个分子的球棍模型。

由于小宏的微型机器人很灵活，这些球型端点可以在空间中任意移动，同时连接相邻两个球型端点的边可以任意的伸缩，这样一个玩具可以变换出不同的形状。在变换的过程中，边不会增加，也不会减少。
小宏想给他的玩具染上不超过k种颜色，这样玩具看上去会不一样。如果通过变换可以使得玩具变成完全相同的颜色模式，则认为是本质相同的染色。现在小宏想知道，可能有多少种本质不同的染色。

【输入格式】
输入的第一行包含三个整数n, m, k，
分别表示小宏的玩具上的端点数、边数和小宏可能使用的颜色数。端点从1到n编号。
接下来m行每行两个整数a, b，表示第a个端点和第b个端点之间有一条边。输入保证不会出现两条相同的边。

【输出格式】
输出一行，表示本质不同的染色的方案数。由于方案数可能很多，请输入方案数除10007的余数。

【样例输入】
3 2 2
1 2
3 2
【样例输出】
6
【样例说明】
令(a, b, c)表示第一个端点染成a，第二个端点染成b，第三个端点染成c，则下面6种本质不同的染色：(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 2), (2, 2, 2)。
而(2, 1, 1)与(1, 1, 2)是本质相同的，(2, 2, 1)与(2, 1, 2)是本质相同的。

【数据规模与约定】
对于20%的评测数据，1<=n<=5， 1<=k<=2。
对于50%的评测数据，1<=n<=10, 1<=k<=8。
对于100%的评测数据，1<=n<=10, 1<=m<=45, 1<=k<=30。

资源约定：
峰值内存消耗 < 512M
CPU消耗 < 5000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。