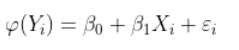R语言进行数据结构化转换：Box-Cox变换、“凸规则”变换方法
原文链接：http://tecdat.cn/?p=22251
线性回归时若数据不服从正态分布，会给线性回归的最小二乘估计系数的结果带来误差，所以需要对数据进行结构化转换。
在讨论回归模型中的变换时，我们通常会简单地使用Box-Cox变换，或局部回归和非参数估计。
这里的要点是，在标准线性回归模型中，我们有
但是有时候，线性关系是不合适的。一种想法可以是转换我们要建模的变量，然后考虑
这就是我们通常使用Box-Cox变换进行的操作。另一个想法可以是转换解释变量，
例如，我们有时会考虑连续的分段线性函数，也可以考虑多项式回归。
“凸规则”变换
“凸规则”(Mosteller. F and Tukey, J.W. (1978). Data Analysis and Regression)的想法是，转换时考虑不同的幂函数。
1.“凸规则”为纠正非线性的可能变换提供了一个起点。
2 .通常情况下，我们应该尝试对解释变量进行变换，而不是对因变量Y进行变换，因为Y的变换会影响Y与所有X的关系，而不仅仅是与非线性关系的关系
3.然而，如果因变量是高度倾斜的，那么将其转换为以下变量是有意义的
更具体地说，我们将考虑线性模型。
根据回归函数的形状（上图中的四个曲线，在四个象限中），将考虑不同的幂。
例如让我们生成不同的模型，看看关联散点图。
> plot(MT(p=.5,q=2),main="(p=1/2,q=2)")
> plot(MT(p=3,q=-5),main="(p=3,q=-5)")
> plot(MT(p=.5,q=-1),main="(p=1/2,q=-1)")
> plot(MT(p=3,q=5),main="(p=3,q=5)")
如果我们考虑图的左下角部分，要得到这样的模式，我们可以考虑
或更一般地
其中
和都大于1.并且
越大，回归曲线越凸。
让我们可视化数据集上的双重转换，例如cars数据集。
> tukey=function(p=1,q=1){
+ regpq=lm(I(y^q)~I(x^p) )
+ u=seq(min(min( x)-2,.1),max( x)+2,length=501)
+ polygon(c(u,rev(u)),c(vic[,2],rev(vic[,3]))^(1/q)
+ lines(u,vic[,2]^(1/q)
+ plot(x^p, y^q )
+ polygon(c(u,rev(u))^p,c(vic[,2],rev(vic[,3])) )
+ lines(u^p,vic[,2])
例如，如果我们运行
> tukey(2,1)
我们得到如下图，
左侧是原始数据集，右侧是经过转换的数据集，
其中有两种可能的转换。在这里，我们只考虑了汽车速度的平方（这里只变换了一个分量）。在该转换后的数据集上，我们运行标准线性回归。我们在这里添加一个置信度。然后，我们考虑预测的逆变换。这条线画在左边。问题在于它不应该被认为是我们的最佳预测，因为它显然存在偏差。请注意，在这里，有可能考虑另一种形状相同但完全不同的变换
> tukey(1,.5)
Box-Cox变换
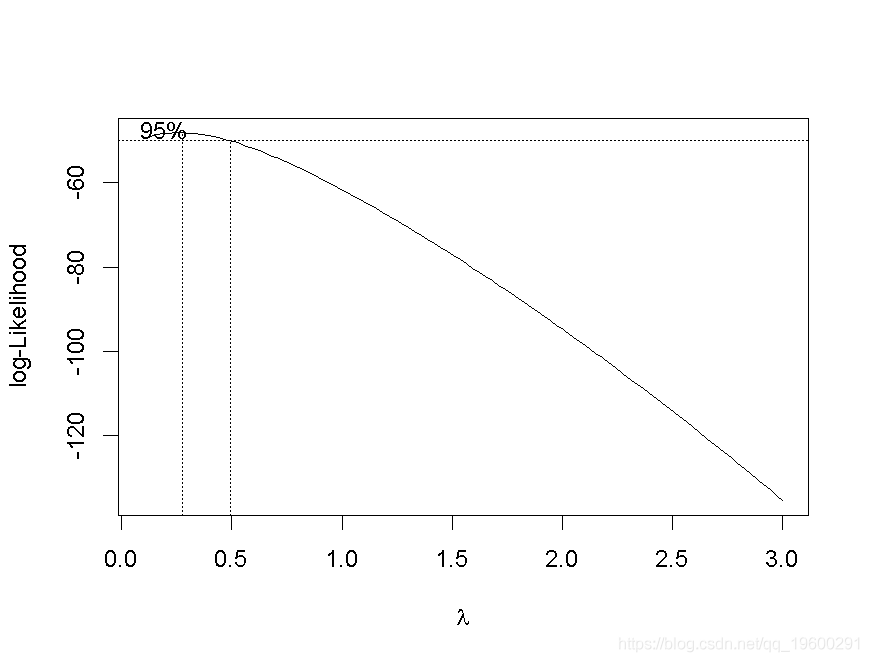
当然，也可以使用Box-Cox变换。此外，还可以寻求最佳变换。考虑
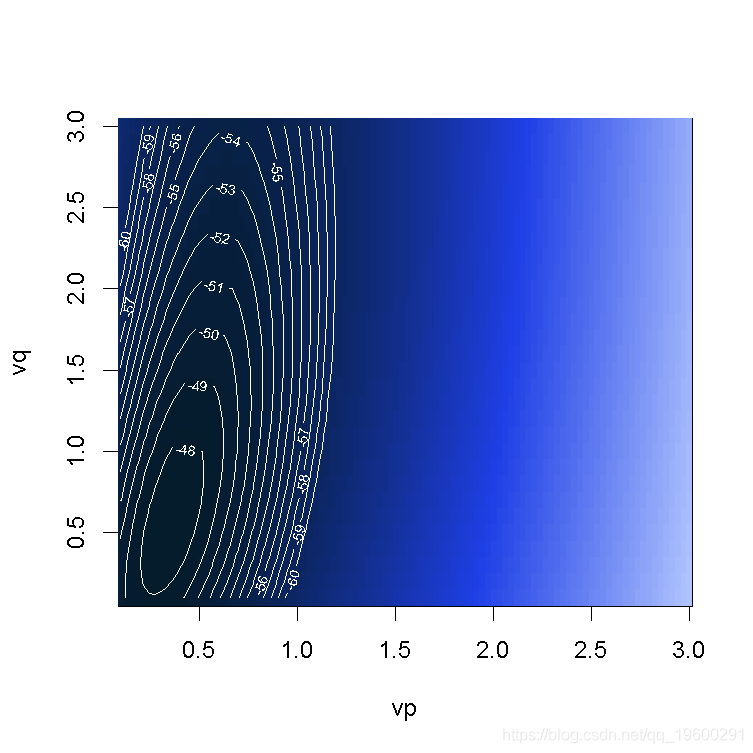
> for(p in seq(.2,3,by=.1)) bc=cbind(bc,boxcox(y~I(x^p),lambda=seq(.1,3,by=.1))$y)
> contour(vp,vq,bc)
颜色越深越好（这里考虑的是对数似然）。 最佳对数在这里是
> bc=function(a){p=a[1];q=a[2]; (-boxcox(y~I(x^p),data=base,lambda=q)$y[50]
> optim(bc,method="L-BFGS-B")
实际上，我们得到的模型还不错，
最受欢迎的见解
1.用R语言模拟混合制排队随机服务排队系统
2.R语言中使用排队论预测等待时间
3.R语言中实现马尔可夫链蒙特卡罗MCMC模型
4.R语言中的马尔科夫机制转换(Markov regime switching)模型
5.matlab贝叶斯隐马尔可夫hmm模型
6.用R语言模拟混合制排队随机服务排队系统
7.Python基于粒子群优化的投资组合优化
8.R语言马尔可夫转换模型研究交通伤亡人数事故预测
9.用机器学习识别不断变化的股市状况——隐马尔可夫模型的应用