手把手教你入门系列 -- 栈（大话数据结构）

栈是限定只在表尾进行删除和插入操作的线性表。

怎么理解“栈”这种数据结构呢？这里举个较为贴切的栗子，手枪就是一个典型的“栈”。

电视节目中的各路英雄在用手枪的时候，通常是先填装子弹，再将弹夹最上层的子弹射出。先进入弹夹的子弹最后射出，后进入弹夹的子弹最先射出，这其实就是栈的思想。

先进后出，后进先出，这就是一种典型的“栈”思想。

这是栈最大的特点，也是栈最大的缺点，因为栈这样的一种特性导致了其只能在同一端插入元素和删除元素。

但我们在前面学了链表，栈能实现的操作链表也都可以实现。我们可以说栈是线性表的一种特例，其中线性表的顺序存储也对应着顺序栈（后面会有链式栈，我还会更的）。与此同时，由于栈涉及的操作比较少，实现起来也较为容易。

看到这里，你可能会发出疑问：有链表了我为什么还要用栈呢？链表能做的事情可比栈多得多了。

一开始我也疑惑，但栈存在就一定有他的道理。对比与链表来说，我认为有两点主要原因：

1. 链表涉及的操作纷杂繁琐，在使用上稍不留神就会出错。
2. 栈在功能上肯定是不如链表全面，但是我们所学的每一种数据结构都不是直接单拎出来讲的，每一种数据结构肯定对应着一种使用场景。在特定的场景之下，栈的实现要比链表简单，这是栈相比链表在时间上的优势。

好吧，说了这么多。栈相比链表来说的优势其实主要就两点：简单容易实现且不容易出错。

那么如何实现“栈”呢？

在实现栈之前，先向大家引入几个概念：

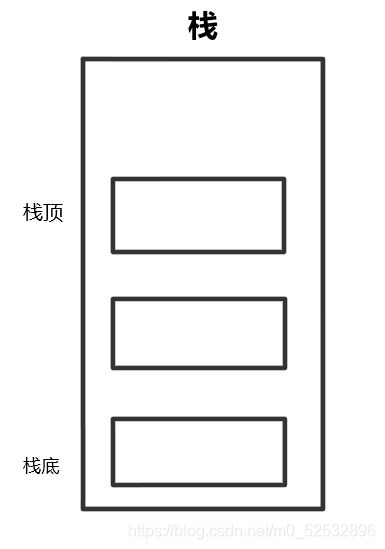
我们把允许插入和删除的一段称为栈顶（表尾），

将另一端称为栈底。

将不含任何数据元素的栈称为空栈。

线性表的顺序存储是依靠数组完成的。这里的顺序栈也与顺序表有着异曲同工之妙。

结合“先进后出，后进先出”的思想，我们将数组的首元素作为栈底元素，将数组的末元素作为栈顶元素，操作时只需要针对栈顶元素即可。

将栈想象为一个容器：

既然栈的操作围绕栈顶元素开展，现在的问题就在于如何表示栈顶元素在数组中的位置？

我们用一个Top变量来表示栈顶元素在数组中的位置，有元素插入到栈顶元素之上，Top就加一，栈顶元素删除后，Top就减一。

结合Top变量来表示栈的几种状态：

（1）栈中有两个元素，Top = 1.

（2）栈中没有元素，Top = -1.

（3）栈中有4个元素（满），Top = 3.

(图画的太丑了，别喷我···)

这里的Top变量实际上代表着栈顶元素的位置，可以理解为一个指针，指向栈顶元素。

但是Top必须小于数组的最大值，而且最小为 0（只有一个元素a[0]）。

如果栈中一个元素也没有，我们通常将Top元素置为 -1。

Top栈顶指针其实和数组下标是一一对应的关系。

看了这么长时间的理论知识，下面我们就可以开始实现栈了：

栈的结构定义

一个数组存数据，一个top变量来表示栈顶元素在栈中的位置。

代码实现：

struct SqStack{
     
	SElemType data[MAX];
	//SElemType 是数据类型，int、float、char都可，根据实际情况决定
	int top;
};

栈的初始化

将top变量置为 -1，表示栈中没有栈顶元素，也就是没有元素。

void InitStack(SqStack *S){
     
	S->top = -1;
}

清除栈

同上。

void ClearStack(SqStack *S){
     
	S->top = -1;
}

检查栈是否为空

如果top变量为 -1，表明栈为空。反之，不为空。

bool EmptyStack(SqStack S){
     
	if(S.top == -1)
		return true;
	else
		return false;
}

返回栈的长度

栈顶元素top代表数组的最后一个元素。

但top是从 0 开始计数的。所以需要返回 top + 1。

int LengthStack(SqStack S){
     
	return S.top + 1;
}

返回栈顶元素值

1. 判断栈是否为空
2. 返回与栈顶指针对应数组的值

Status GetTop(SqStack S,SElemType *e){
     
	if(S.top == -1)
		return ERROR;
	else 
		*e = S.data[S.top];
		return OK;
}

在栈顶插入元素

1. 判断栈是否已满
2. 如果栈未满，栈顶指针加一
3. 对与栈顶指针对应的数组元素赋值

Status Push(SqStack *S,SElemType e){
     
	if(S->top == MAX - 1)
		return ERROR;
	S->top++;
	S->data[S->top] = e;
	return OK;
}

删除栈顶元素

1. 判断栈是否为空
2. 保留栈顶指针对应元素的值
3. 栈顶指针加一

Status Pop(SqStack *S,SElemType *e){
     
	if(S->top == -1)
		return ERROR;
	*e = S->data[S->top];
	S->top--;
	return OK;
}

加入测试后的全部代码：

#include

#define OK 1
#define ERROR 0
#define MAX 20

typedef int Status; 
//Status表示函数返回值的类型，OK代表函数成功运行，ERROR代表运行出错
typedef int SElemType; 
//SElemType类型根据实际情况而定，这里假设为 int 

struct SqStack{
     
	SElemType data[MAX];
	int top;
};

void InitStack(SqStack *S){
     
	S->top = -1;
}

void ClearStack(SqStack *S){
     
	S->top = -1;
}

bool EmptyStack(SqStack S){
     
	if(S.top == -1)
		return true;
	else
		return false;
}

int LengthStack(SqStack S){
     
	return S.top + 1;
}

Status GetTop(SqStack S,SElemType *e){
     
	if(S.top == -1)
		return ERROR;
	else 
		*e = S.data[S.top];
		return OK;
}

Status Push(SqStack *S,SElemType e){
     
	if(S->top == MAX - 1)
		return ERROR;
	S->top++;
	S->data[S->top] = e;
	return OK;
}

Status Pop(SqStack *S,SElemType *e){
     
	if(S->top == -1)
		return ERROR;
	*e = S->data[S->top];
	S->top--;
	return OK;
}

void StackTraverse(SqStack S){
     
	int i = 0;
	while(i <= S.top){
     
		printf("%d ",S.data[i]);
		i++;
	}
	printf("\n");
}


int main(){
     
    int e;
    SqStack S;
    InitStack(&S);
    for(int i = 1; i <= 10 ;i++){
     
    	Push(&S,i);
	}
	printf("栈顶元素依次为： ");
	StackTraverse(S);
	Pop(&S,&e);
	printf("弹出的栈顶元素为: %d\n",e);
	if(EmptyStack(S))
		printf("栈为空\n");
	else
		printf("栈不为空\n");
	GetTop(S,&e);
	printf("栈顶元素为 %d，栈的长度为 %d\n",e,LengthStack(S));
	ClearStack(&S);
	if(EmptyStack(S))
		printf("栈为空\n");
	else
		printf("栈不为空\n");
	
    return 0;
}

运行结果：

后续我还会将继续更新，喜欢的话给点个赞吧！！！