数据结构第四周作业(栈、队列、递归)
1.
元素a, b, c, d顺序入栈,请写出出栈时的所有可能的顺序和按栈操作不可能出现的序列。
应该有14种情况( C 4 8 − C 5 8 = 14 C_4^{8} - C_{5}^{8} = 14 C48−C58=14)
a第一个出栈:abcd; acbd; acdb; abdc; adcb;
a第二个出栈:bacd; badc;
a第三个出栈:cbad; bcad;
a第四个出栈:bcda; cbda; cdba; bdca; dcba;
不可能出现的序列:
adbc; cabd; cadb; dacb; dabc;
cdab; dcab; bdac; dbac; dbca;
通过归纳法可以得出的是n个数依次出栈的出栈顺序满足

这个实际上是卡特兰数(Catalan number)卡塔兰数的通项公式为 h ( n ) = C ( 2 n , n ) − C ( 2 n , n + 1 ) ( n = 0 , 1 , 2 , . . . ) 。 h(n)=C(2n,n)-C(2n,n+1)(n=0,1,2,...)。 h(n)=C(2n,n)−C(2n,n+1)(n=0,1,2,...)。
2.
编写算法,用两个大小相同的栈来模拟一个队列的操作(包括入队操作和出队操作两个算法) 。
#include 3.
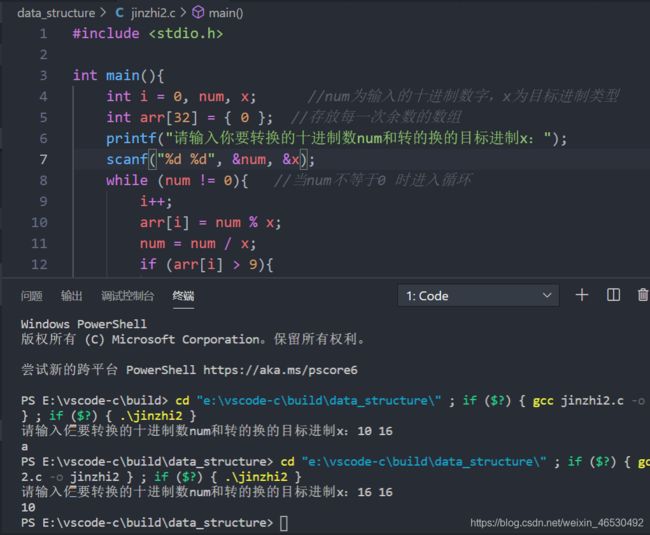
编写一个非递归算法,将十进制数转换成十六进制数,并输出转换后的数。
#include 16进制的数主要问题在于大于10的话要用对应的字母来表示,所以多加一条语句,把数字当做对应的字符来存储并打印。
4.
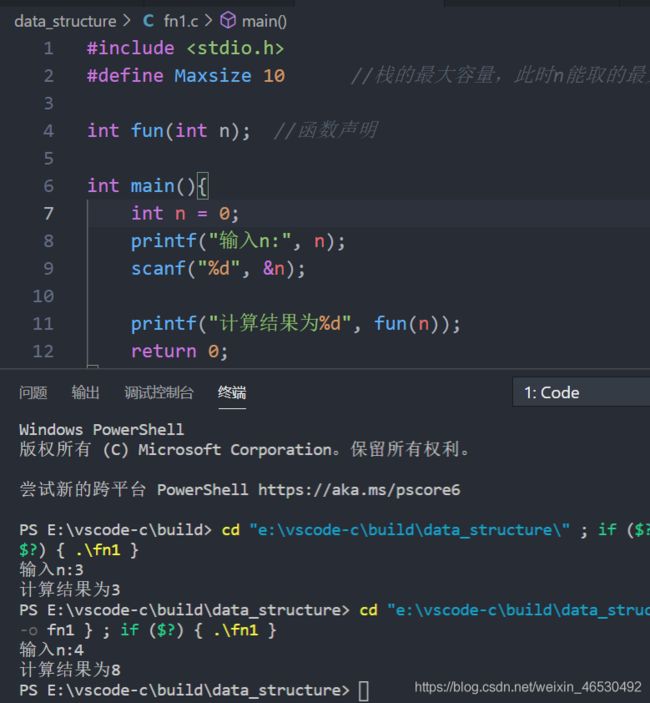
编写一个非递归算法,利用栈计算如下函数的值:
f ( n ) = n + 1 f(n) = n+1 f(n)=n+1 当 n=0时;
f ( n ) = n ∗ f ( [ n / 2 ] ) f(n) = n*f([n/2]) f(n)=n∗f([n/2]) 当 n>0时。
#include 递归算法
#include