人工智能-数学基础-傅里叶变换与卷积

一.周期函数

周期函数可以进行傅里叶展开:
$$f(x)=a_0+\sum (a_n\sin (2\pi nx)+b_n\cos (2\pi nx))$$

"""
1.周期函数
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

x = np.linspace(0, 2 * np.pi, 10000)
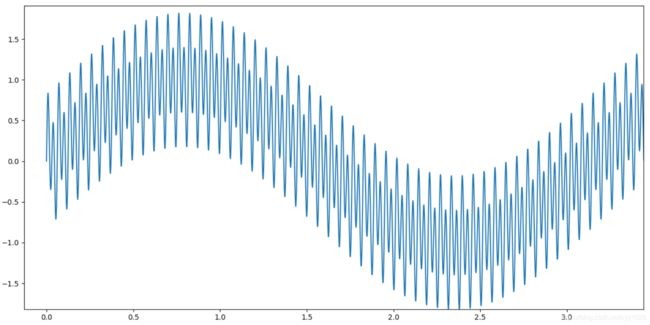
y = np.sin(x * 2) + np.sin(100 * x) * 0.3
plt.plot(x, y)
plt.show()

图中函数包含有高频信息和低频信息, 整个大的周期曲线称为低频, 小的周期曲线称为高频

二.傅里叶变换

2.1 连续数据傅里叶变换

傅⾥叶变换假设被变换的函数（或称为信号） x(t)是连续的，并且是非周期的，此时定义⼀个变换：
$$X(\omega )=F(x(t))={\int }_{-\infty }^{+\infty }x(t)e^{-i\omega t}dt$$
$$此时称X(\omega )为频谱，此公式将函数x(t)由时间域（时间t为⾃变量）变换到了频率域（以\omega 为⾃变量）$$

2.1.1 下面看下对函数 f(x) = sin(2x) + 0.3sin(100x)+ 0.6sin(200x)进行傅里叶变换:
原始图像:

"""
原始函数图像
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

x = np.linspace(0, 2 * np.pi, 10000)
y = np.sin(x * 2) + np.sin(100 * x) * 0.3 + np.sin(200 * x) * 0.6

plt.plot(x, y)
plt.show()

此函数包含一个低频,一个次高频,一个高频信号

进行傅里叶变换:

"""
傅里叶变换
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

x = np.linspace(0, 2 * np.pi, 10000)
y = np.sin(x * 2) + np.sin(100 * x) * 0.3 + np.sin(200 * x) * 0.6

# 进行傅里叶变换(此时f为频谱)
f = np.fft.fft(y)
# 傅里叶变换后此时f为复数域域,将之变成实数域
plt.plot(np.abs(f))
plt.show()

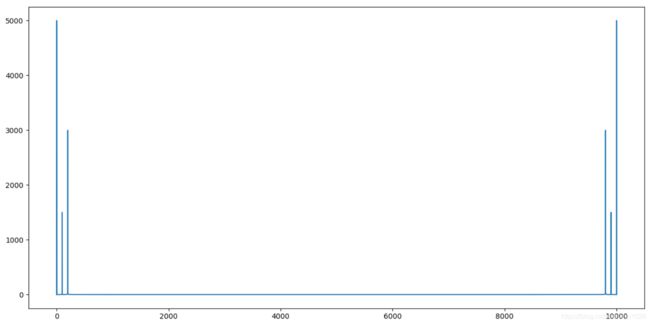
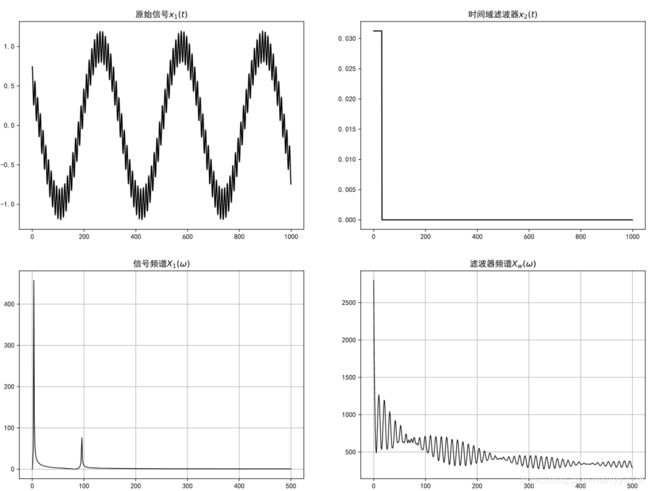
放大一下:

我们会发现,在2,100,200的值上,分别得出了低频,次高频,高频的最大值

2.2.连续数据傅里叶反变换与滤波

也可以通过反变换将频率域的函数反变换为时间域：
$$x(t)=F^{-1}(X(\omega ))=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(\omega )e^{i\omega t}d\omega$$
二中的函数存在低频、次高频和高频信号, 如果我们想去掉高频信号, 或者次高频或高频信号的话,可以利用傅里叶反变换

2.2.1 过滤低频信号

"""
傅里叶反变换
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

x = np.linspace(0, 2 * np.pi, 10000)
y = np.sin(x * 2) + np.sin(100 * x) * 0.3 + np.sin(200 * x) * 0.6

# 进行傅里叶变换(此时f为频谱)
f = np.fft.fft(y)
# 将低频信息附近的值设为0(3与-3是根据二中频谱图像得出)
f[:3] = 0
f[-3:] = 0

# 进行傅里叶的反变换
y = np.fft.ifft(f)
# 取实数域部分
y = np.real(y)

plt.plot(x, y)
plt.show()

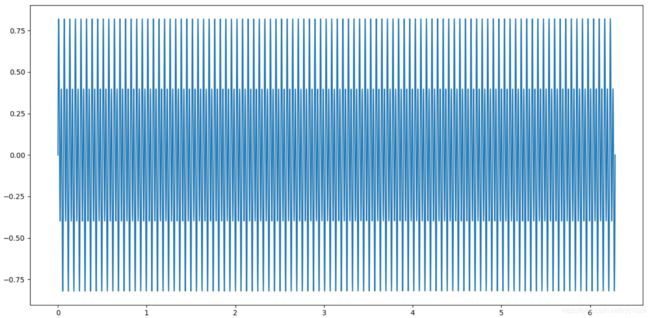
可以看到, 此时低频信号已经被过滤掉了. 这里叫做高通滤波, 相当于傅里叶展开,只保留高阶系数

2.2.2 过滤高频信号

"""
傅里叶反变换
"""
import numpy as np
import matplotlib.pyplot as plt

plt.switch_backend("TkAgg")

x = np.linspace(0, 2 * np.pi, 10000)
y = np.sin(x * 2) + np.sin(100 * x) * 0.3 + np.sin(200 * x) * 0.6

# 进行傅里叶变换(此时f为频谱)
f = np.fft.fft(y)
# 将低频信息附近的值设为0(3与-3是根据二中频谱图像得出)
f[4:250] = 0
f[-250:-4] = 0

# 进行傅里叶的反变换
y = np.fft.ifft(f)
# 取实数域部分
y = np.real(y)

plt.plot(x, y)
plt.show()

此时高频与次高频的信号被过滤了, 只剩下低频信号,叫做低通滤波. 相当于傅里叶展开,只保留低阶系数

2.3.离散数据傅里叶反变换与滤波器

在⼯程实践中绝⼤部分使⽤的均是离散傅⾥叶变换，即现在计算机处理中所谓的傅⾥叶变换信号和频谱都是周期性的，均是离散的。

1.连续傅⾥叶变换信号和频谱都是非周期性的；
2.周期信号的频谱是离散的；
3.离散信号的频谱是周期性的；
4.离散傅⾥叶变换（Discrete Fourier Transform，DFT）的信号和频谱都是周期性的；

离散傅⾥叶变换计算公式:
$$X(k)=\sum _{n=0}^{N-1}x(n)e^{-i\frac{2\pi n}{N}k}$$
反变换公式:
$$x(k)=\frac{1}{N}\sum _{n=0}^{N-1}X(n)e^{i\frac{2\pi n}{N}k}$$

二.傅里叶变换与卷积

傅⾥叶变换的另外⼀个作⽤就是滤波
$$假设两个信号x_1(t),x_2(t)以及其傅⾥叶频谱X_1(\omega ),X_2(\omega )$$
$$两个频谱进行相乘：X_3=X_1(\omega )X_2(\omega )$$
$$X_3为滤波后的信号,频谱相乘等于时间阈上的卷积(也是折积)$$
$$等价于：x_3(\tau )=x_1(t)\ast x_2(t)=={\int }_{-\infty }^{+\infty }{x}_1(\tau )x_2(t-\tau )d\tau$$
$$时间域上的卷积可以代替频谱相乘方式的滤波$$$$时间域卷积计算即是频率域乘法计算$$

进行卷积后得出:

"""
卷积
"""
import matplotlib.pyplot as plt
import numpy as np

plt.switch_backend("TkAgg")

# 设置plt可以写中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


# x1称为信号, x2称为滤波器(也称卷积核心), 卷积也称为时间域滤波
def conv(x1, x2):
    # 根据卷积公式, 将x2翻转
    x2 = x2[::-1]
    l1 = len(x1)
    l2 = len(x2)
    x3 = np.zeros([l1])
    for i in range(l1 - l2 + 1):
        x3[i] = np.sum(x1[i:i + l2] * x2)
    return x3


x1 = np.linspace(-5, 5, 1000)
y1 = np.sin(2 * x1) + 0.2 * np.sin(60 * x1)

# 绘制函数
plt.subplot(121)
plt.plot(x1, y1)
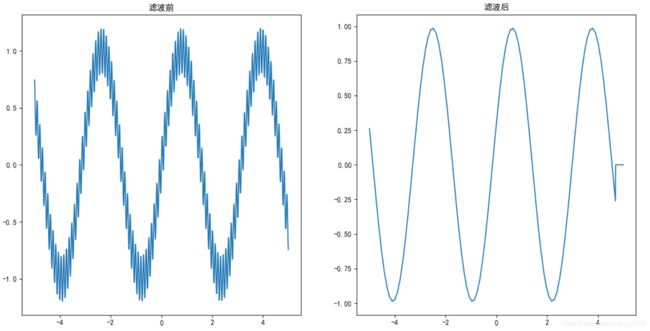
plt.title("滤波前")

# 设置滤波器
g = np.ones([32]) / 32
# 进行卷积计算
y1 = conv(y1, g)

plt.subplot(122)
plt.title("滤波后")
plt.plot(x1, y1)
plt.show()

以上为一维数据处理

三.图像数据处理

图像数据可以看成是二维数据.我们先看一下图像数据是什么样的:

利用opencv库进行图像处理.安装库:

 pip install opencv-python

用我们喜爱的姚明举下例子 ^ . ^：

import cv2

# 读取图片
img = cv2.imread("ym.png")
# 打印图像信息
print(img.shape, img.dtype)
# 展示图片
cv2.imshow("img", img)
# 等待输入字符才会终止程序
cv2.waitKey(0)

打印的图片信息和类型:

(574, 766, 3) uint8

其中小括号里的574、766、3分别代表高、宽和颜色的三原色(顺序为蓝，绿，红)，uint8表示8位的无符号整形, 表示该矩阵中每一个数字都是8位的。

3.1 过滤颜色

import cv2

# 读取图片
img = cv2.imread("ym.png")
# 打印图像信息
print(img.shape, img.dtype)

# 将蓝和红设置为0，只留绿色
img[:, :, 0] *= 0
img[:, :, 2] *= 0

# 展示图片
cv2.imshow("img", img)
# 等待输入字符才会终止程序
cv2.waitKey(0)

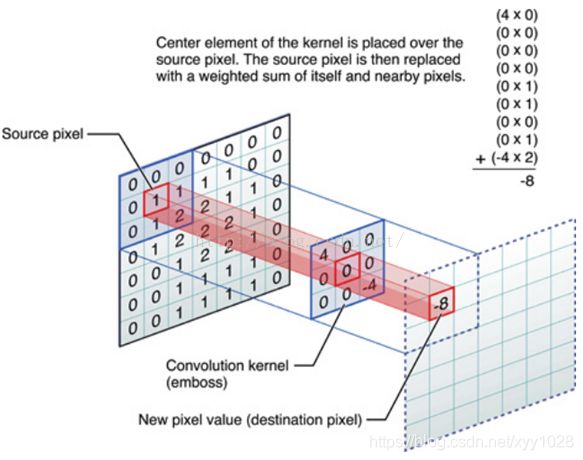
3.2 图像的卷积

3.2.1 平均模糊

import cv2 
import numpy as np 

# 滤波器，平均模糊
kernel = np.ones([16, 16]) / (16*16)

img = cv2.imread("ym.png")
# 进行滤波（卷积运算）， -1 代表对每一个颜色单独的进行处理
img = cv2.filter2D(img, -1, kernel)
cv2.imshow("img", img)
cv2.waitKey(0)

3.2.2 边界滤波
一般图像中可以通过物体的颜色，来区分不同的物体，那么我们在设置滤波器的时候，可以将相同颜色的像素点进行过滤，只保留物体边缘处颜色不一样的地方。

提取纵向边界，可以看到纵向部分更突出了:

import cv2 
import numpy as np 

# 提取纵向边界
kernel = np.ones([4, 4])
kernel[:, :2] = -1
"""
[[-1. -1.  1.  1.]
 [-1. -1.  1.  1.]
 [-1. -1.  1.  1.]
 [-1. -1.  1.  1.]]
"""

img = cv2.imread("ym.png")
img = cv2.filter2D(img, -1, kernel)
cv2.imshow("img", img)
cv2.waitKey(0)

提取横向边界，可以看到横向边界更突出了:

import cv2 
import numpy as np 

# 提取横向边界
kernel = np.ones([4, 4])
kernel[:2, :] = -1
"""
[[-1. -1. -1. -1.]
 [-1. -1. -1. -1.]
 [ 1.  1.  1.  1.]
 [ 1.  1.  1.  1.]]
"""

img = cv2.imread("ym.png")
img = cv2.filter2D(img, -1, kernel)
cv2.imshow("img", img)
cv2.waitKey(0)

3.2.3 更复杂的滤波，例如浮雕滤波

import cv2 
import numpy as np 

# 浮雕滤波
kernel = np.array([[-2, -1, 0], 
                   [-1, 1, 1], 
                   [0, 1, 2]])
img = cv2.imread("ym.png")
img = cv2.filter2D(img, -1, kernel)
cv2.imshow("img", img)
cv2.waitKey(0)

3.2 视频处理

我们同样可以对视频进行卷积过滤

import cv2 
import numpy as np 

# 滤波器，平均模糊
kernel = np.ones([16, 16]) / (16*16)

# 读取摄像的句柄,调去第一个摄像头
cap = cv2.VideoCapture(0) 
# 构建读取循环
while True:
    ret, img = cap.read()
    img = cv2.filter2D(img, -1, kernel)
    cv2.imshow("img", img)
    # 每隔100ms没响应则继续读取
    ret = cv2.waitKey(100)
    if ret == 97:
        break
cv2.destroyAllWindows()