3.过滤——简单移动平均线概念(SMA)、SMA的假设、加权移动平均线概念(WMA)_1
目录
移动平均线的概念(SMA)
SMA的假设
噪音能消除吗?
加权移动平均线的概念(WMA)
移动平均线的概念(SMA)
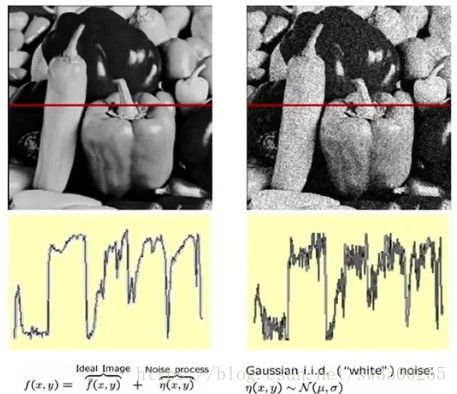
上次我们谈到,在图像函数中添加了一个噪声函数,所以这里我们得到的噪声,定义为sigma缩放的随机事物,
我们的输出只是图像加上噪声。
>> noise = randn(size(img)) .* sigma;
>> output = img + noise;记住,你必须担心图像范围内sigma的大小,所以如果你的图像是0到255,sigma 为5可能是合理的。
如果你的图像变为0到1, sigma的大小为5就不合理了,所以你要担心它们是如何组合在一起的。
——现在,假设你的图像中有噪音,你想要消除噪音,你会怎么做?
现在我确定,你们中的一些人有类似的建议。
在这里,这是典型的一个:让我根据周围像素的平均值,替换每个像素值。
接下来。让我们先考虑1D中的情况,然后我们再进入2D的情况,
我们将讨论为什么用这个方法是正确,还会讨论什么时候不能这么用这个方法。
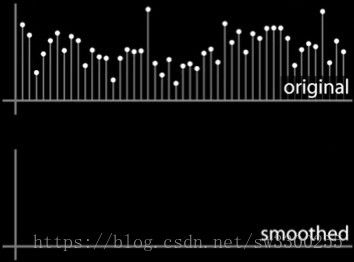
这是我们的第一次尝试,我们要用像素邻域值的平均值来替换每个像素,这被称为移动平均线(SMA)。
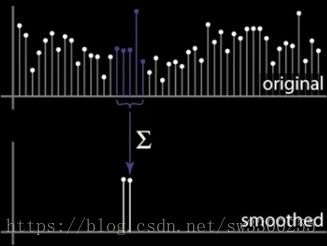
这里我有一些位置,我只取平均值,然后把它放在那里:
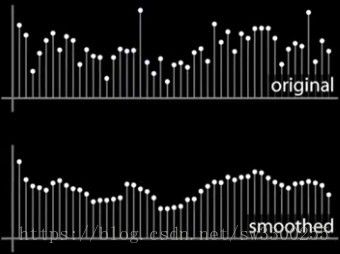
然后移动我的小窗口,取平均值,得到新的值,然后继续移动小窗口,取平均值,得到新的值,一直循环下去,
最终,我会得到这个新的平滑版本的原版,平滑的意思是我们在本地平均。
以下有具体教你怎么计算移动平均线的相关视频:(最好看视频操作一遍)
https://www.youtube.com/watch?v=Qu-EpmEkS9Q
SMA的假设
好吧,那不是火箭科学,这似乎是合理的。
但要问的一个重要问题,为什么这个解决方案对你来说是直观的?
为什么你说,为了摆脱一些噪音,我会采取一点平均值?你对图片的假设是什么,顺便说一下,对噪音的假设是什么。
好吧,我想出来了,你在做了一些关键性的假设:
第一个假设:像素的实际值可能类似于附近的值;
如果不是这样,为什么我会使用附近的像素来试图弄清楚我的真实价值是多少?所以这是第一个假设。
第二个假设,对于某些已经了解的人来说,只是数学方面的问题。
第二个假设:每一个被添加到每个像素的噪声与被添加到所有其他像素的噪声无关。
这意味着如果我只取噪声的平均值,那它将趋近于零。
也就是说,有时它会上升,有时会下降,如果我在它们周围取平均值,最后那将是零。
因此,如果附近有大约相同值的像素是相关的,而且噪声是独立的,这种情况使用平均值是最好的。
噪音能消除吗?
小测试:
如果噪声只是添加到图像的函数,我们可以通过再次减去噪声来消除噪声。
A、正确,我们可以做到这一点;
B、正确,但我们不知道噪声函数,所以我们实际上不能进行消去;
C、当您将噪音放入某物时,它会破坏图像中的信息,并且无法恢复它。
是的,如果您告诉我噪音是什么,我可以消除噪音,但没有人告诉你噪音是什么。
因为如果他们这么做了,他们会把它从一开始就移除。所以你不知道噪音是什么。你只知道噪音的统计数字。
然后,这是一个有趣的。我们来看看C描述:
是的,因为加性噪声破坏信息。如果你只是简单的加法,加法是有效的,那么这个陈述是不正确的。
所以,C会是错的。但是,假设您的限制在0到255之间,甚至在0到1之间。
如果你的噪音把你推到极限之外并且你剪辑,你将丢失了这些信息。
所以有时当你添加噪声时,你会得到这些非线性。
但总的来说,我们无法消除噪音,因为我们不知道噪音是什么。
如果我们知道,我们可以减去它。
加权移动平均线的概念(WMA)
让我们重温一下我们的加权平均法。
所以,不要只考虑平均局部像素,让我们把它想象成一组权重,我们要做的是我们要用一组权重来加权所有这些像素,
并且我们将使用这些权重将它们组合起来以得出新值。
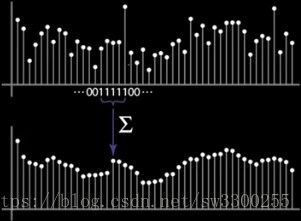
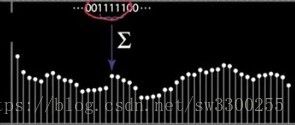
现在,当我们只是做移动的盒子时,我们的权重只是,我们说它是五个长,它们将五个五分之一,如图:
可以看到下方的1D图的平均值等于上方的1D图五个1相加后除以5的结果:
![]()
上图的权重是均匀分布的。但这有意义吗?
还记得我们假设附近的像素与我的价值有关吗?
还有另一个相关的假设:
你附近越多值,你就越相关。这意味着离我更近的像素应该对平均值贡献更多。
那么让我们改变我们的移动平均线!
之前,如果你还记得,我们有这些均匀的权重吗? [1,1,1,1,1] / 5。
如果我们想使用一些不均匀的权重怎么办?
这里有一个集合:
![]()
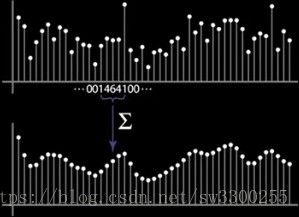
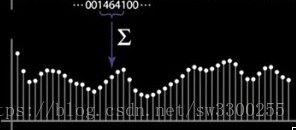
我要将这些权重从均匀变为不均匀,我希望你看看下面图片会发生什么。
这是均匀的权重,如图:
而这是非均匀的权重,中心加权,如图:
你可以对比两张图,你会发现非均匀的表现更平滑。
非均匀权重有这样的假设:中心值附近像素越多,中心值应该具有的权重越大。
以下有具体教你怎么计算 加权移动平均线 的视频:(最好看视频操作一遍)
https://www.youtube.com/watch?v=DipOB2H6ick
小测验:
如果你要做加权移动平均计算,你的权重应该是什么?
A,奇数,因为中间像素更容易。
B,即便如此,它可以在我周围对称。
C,显然是偶数或奇数。
对于我们大多数人来说,我们倾向于使用奇数大小的权重集。
——学会编写自己的代码,才能练出真功夫。