pytorch使用教程及应用-GANS编程(3)-改良神经网络及小结

4.改良神经网络

1.损失函数

​ 有时候，我们会把一些神经网络的输出值设计为连续范围的值。例如，一个预测温度的网络会输出0~100°C的任何值。

​ 也有时候，为你们会把网络设计成输出true/False(1/0)，也就是**binary classfication.**例如，我们要判断一副图像是不是猫，输出值应该尽量接近0.0或1.0,而不是介于两者之间。

​ 如果我们针对不同情况设计损失函数，会发现均方误差只适用于第一种情况。第一种任务叫做回归(regression)，这个相信大家都知道。

对于第二种情况，也就是分类问题(classfication)，我们往往使用二元交叉熵损失(binary cross entropy loss)，它同时惩罚置信度(confidence)高的错误输出和置信值低的正确输出。pytorch将其定义为nn.BCELoss()。

​ 我们的网络对MNIST图像进行分类，属于第二种类型。在理想情况下，输出节点中应该只有一个接近1.0，其他全部接近0.0.

self.loss_function=nn.BCELoss()

大家可以修改后，再跑一次自己的网络，相信性能得分会有所提升。

1. 我们可以看到，损失值的确在下降，不过下降的速度比MSELoss()慢。损失值的噪声也更大，以至于在训练的后期偶尔也有较高的损失值出现。

2. 但是最后的得分是上升了的，说明网络的总体性能确实是上升了。
3. 目前为止的完整代码：

import torch
import torch.nn as nn
import pandas
import time
import matplotlib.pyplot as plt
from torch.utils.data import Dataset
class Classifier(nn.Module):
    def __init__(self): #类似于java的构造函数，当我们从一个类中创建对象时其就会自动被调用
        #初始化pytorch父类
        super().__init__()  #继承调用父类的构造函数，然后pytorch.nn模块会为我们设置分类器 一般这个步骤都是必要的，需要通过继承底层的父类的基本属性然后再在后面进行自定义（特定的) 的扩展
    #现在开始设计神经网络，设计神经网络结构有很多种方法
    #我们可以使用nn.Sequential(),它允许我们提供了一个网络模块的列表。模块必须按照我们希望的信息传递顺序添加到容器中。

    #定义神经网络层
        self.model=nn.Sequential(
            nn.Linear(784,200), #一个从784个节点到200个节点的全连接映射。这个模块包含节点之间链接的权重，在训练时会被更新。
            nn.Sigmoid(),#将S型逻辑函数函数应用于前一个模块的输出，也就是本例中200个节点的输出
            nn.Linear(200,10),#一个将200个节点映射到10个节点的全连接映射。它包含中间隐藏层与输出层10个节点之间所有链接的权重。
            nn.Sigmoid()#再将S型逻辑激活函数应用于10个节点的输出。其结果就是网络的最终输出。也就是我们需要的分类结果。
        )
        self.loss_function = nn.BCELoss()

        # 创建优化器，使用简单的梯度下降
        self.optimiser = torch.optim.SGD(self.parameters(), lr=0.01)

        # 记录训练进展的计数器和列表
        self.counter = 0
        self.progress = []
        pass  # Python pass 是空语句，是为了保持程序结构的完整性。
        # pass 不做任何事情，一般用做占位语句。
        pass
    def forward(self,inputs):
#直接运行模型
        return self.model(inputs)
    def train(self,inputs,targets):
# 计算网络的输出值
        outputs=self.forward(inputs)
# 计算 cost
        loss=self.loss_function(outputs,targets)
#pytorch简化了我们自己造轮子时需要为每个节点计算误差梯度，再更新链接权值。
# 梯度归零，反向传播，并更新权重
        self.optimiser.zero_grad() #将计算图中的梯度全部归0，也就是我们的初始化
        loss.backward() #从loss函数中反向传播计算梯度
        self.optimiser.step() #使用这些梯度来更新网络的可学习参数
#在每次训练网络之前，我们都需要将梯度归零。否则，每次loss.backward()计算出来的梯度会累积。
#在train()函数中，我们可以每隔10个训练样本增加一次计数器的值，并将损失值添加进列表的末尾。
#每隔10个训练样本增加一次计数器的值，并将损失值添加进列表的末尾
        self.counter += 1
        if(self.counter%10 ==0):
	        self.progress.append(loss.item()) #item函数方便我们展开一个单值张量，获取里面的数字
	        pass
#方便了解训练目前的进展快慢
        if(self.counter%10000==0):
	        print("counter =",self.counter)
	        pass

    # 将损失值可视化绘制成图，我们可以在神经网络类中添加一个新函数plot_progress()
    def plot_progress(self):
         df = pandas.DataFrame(self.progress, columns=['loss'])  # 将损失值列表progress转换成一个pandas DataFrame对象
         df.plot(ylim=(0, 1.0), figsize=(16, 8), alpha=0.1, marker='.',  # 使用plot()函数的选项，设计图的设计和风格
         grid=True, yticks=(0, 0.25, 0.5))
         plt.show()
         pass
class MnistDataset(Dataset):
    def __init__(self,csv_file):
        self.data_df=pandas.read_csv(csv_file,header=None)
        pass
    def __len__(self):
        return len(self.data_df)
    def __getitem__(self, index):
  #目标图像（标签）
        label=self.data_df.iloc[index,0] #从数据集中的第index项中提取该数字的标签-也就是该数字具体是多少
        targets=torch.zeros((10))   #初始化都为0，最后的结果应该为除了与标签相对应的项是1之外，其他值皆为0.比如，标签0所对应的张量是[1,0,0,0,0,0,0,0,0,0] 这种表示方法叫做 one-hot encoding
        targets[label]=1.0

        #图像数据，取值范围是0~255，标准化为0~1
        image_values=torch.FloatTensor(self.data_df.iloc[index,1:].values)/255.0  #将图像像素值标准化
        #返回标签、图像数据张量以及目标张量
        return label,image_values,targets
    #添加一个可视化函数
    def plot_image(self,index):
        arr=self.data_df.iloc[index,1:].values.reshape(28,28)
        plt.title("label="+str(self.data_df.iloc[index,0]))
        plt.imshow(arr,interpolation='none',cmap='Blues')
        plt.show()
        pass
    pass
if __name__ == '__main__':
    mnist_dataset=MnistDataset('mnist_train.csv')
    mnist_test_dataset=MnistDataset('mnist_test.csv') #mnist_test_dataset有1万条数据
    t0=time.time()
    count=0
    #创建神经网络
    C=Classifier()
    #训练网络的代码同样很简单：
    #在Mnist数据集训练神经网络
    epochs=3
    for i in range(epochs):
        print('training epoch',i+1,"of",epochs)
        for label,image_data_tensor,target_tensor in mnist_dataset:
            C.train(image_data_tensor,target_tensor)
            pass
        print(str(count+1)+'个周期的训练耗费了'+str(time.time()-t0)+'s')
        count+=1
        pass
    C.plot_progress()
   # plt.show()
    # record=19
    # image_data=mnist_test_dataset[record][1]  #默认使用getitem方法 该方法已被覆写
    # output=C.forward(image_data)
    # pandas.DataFrame(output.detach().numpy()).plot(kind='bar',legend=False,ylim=(0,1))
    # plt.show()
    # 测试用训练数据训练后的网络

    score = 0
    items = 0

    for label, image_data_tensor, target_tensor in mnist_test_dataset:
        answer = C.forward(image_data_tensor).detach().numpy()
        # argmax返回向量中最大值的索引
        if (answer.argmax() == label):
            score += 1
            pass
        items += 1
        pass
    print(score, items, score / items)
    
    
 output:
    9031 10000 0.9031

2.激活函数

​ S型逻辑函数在神经网络发展的早期被广泛使用，因为它的形状看起来比较符合自然界中的实际情况。科学家们普遍认为，动物的神经元之间在传递信号时，也存在一个类似的阈值。此外，也因为在数学上它的梯度较容易计算。更加详细的声明欢迎大家查看我的其他博客。

​ 然而，它具有一些缺点。最主要的一个缺点是，在输入值变大时，梯度会变得非常小甚至消失。这意味着，在训练神经网络时。如果发生这种饱和(saturation)，我们无法通过梯度来更新链接权重。

(weights)

​ 还有其他很多可选的激活函数。例如relu和 leaky relu。具体的函数图像大家可以查看我的神经网络方面的学习笔记。总之，它们两个主要是线性激活函数，所以不会存在梯度消失或者说饱和这种问题。

我们将损失函数重置为MSELoss()，并将激活函数改为LeakyReLu(0.02),其中0.02是函数左半边的梯度。

# 定义神经网络层
self.model-nn.Sequential(
	nn.Linear(784,200),
	nn.LeakyReLU(0.02),
	nn.Linear(200,10),
	nn.LeakyReLU(0.02)
)

经过修改后，输出结果如下：

最新的模型准确率达到了97%左右，且振荡下降许多，所以说明改善激活函数有不错的效果。

但值得注意的是，这里我们重新使用了MSELoss()，因为用leakyrelu 函数可能意味着我们更倾向于以回归的思想来解决该问题。

3.改良优化方法

随机梯度下降的一个典型缺点是，它会陷入损失函数的局部最小值(local minima).还有一个缺点是，它对所有可学习的参数都使用单一的学习率。

所以，一个常见的不错方法是Adam优化算法，其利用了动量(momentum)的概念，详情可以查看我的博客来对其进一步理解。

https://blog.csdn.net/weixin_45870904/article/details/114047424?spm=1001.2014.3001.5501

https://blog.csdn.net/weixin_45870904/article/details/114075281?spm=1001.2014.3001.5501

Adam优化算法优点：

1. 利用动量的思想，减少陷入局部最小值的可能性。

2. 对每个可学习参数使用单独的学习率，这些学习率随着每个参数在训练期间的变化而改变。

   事实上，我觉得这个地方有问题，应该是对每个可学习参数使用单独的梯度，梯度会变化。

   而学习率作为一个超参数，我并不觉得能够在训练过程中随便修改。

事实上，在pytorch的源码中对于adam优化算法的描述中也只是将lr默认设置成为了一个很小的值。

我们来看看修改优化方法的结果如何吧：

9597 10000 0.9597

这次效果略差，我想应该与我选择的激活函数有关系。一般来说，中间层使用leaky relu ，输出使用sigmoid() 会更加科学有效。

4.标准化

仍然是一个新技术！

https://zhuanlan.zhihu.com/p/54530247

大家可以看看这篇文章了解下batch norm和layer norm

这里就先不多做赘述

什么是normalization

我们这里先讲一下简单的对于输入的normalization，其实就是消除输入的量纲，将其变为一个类似于标准正态分布的东西，经过大量实验数据表明，这样做对于神经网络的训练是有很大好处的，而且可以方便我们去控制输出范围。

优化：

     self.model=nn.Sequential(
            nn.Linear(784,200), #一个从784个节点到200个节点的全连接映射。这个模块包含节点之间链接的权重，在训练时会被更新。
            nn.LeakyReLU(0.02),#将S型逻辑函数函数应用于前一个模块的输出，也就是本例中200个节点的输出
            nn.LayerNorm(200),#我们只设计了一个隐藏层，所以这个东西用于将第一步激活函数计算出的结果进行归一化
            nn.Linear(200,10),#一个将200个节点映射到10个节点的全连接映射。它包含中间隐藏层与输出层10个节点之间所有链接的权重。
            nn.LeakyReLU(0.02)#再将S型逻辑激活函数应用于10个节点的输出。其结果就是网络的最终输出。也就是我们需要的分类结果。
        )

5.优化方法整合：

self.model=nn.Sequential(
    nn.Linear(784,200), #一个从784个节点到200个节点的全连接映射。这个模块包含节点之间链接的权重，在训练时会被更新。
    nn.LeakyReLU(0.02),#将S型逻辑函数函数应用于前一个模块的输出，也就是本例中200个节点的输出
    nn.LayerNorm(200),#我们只设计了一个隐藏层，所以这个东西用于将第一步激活函数计算出的结果进行归一化
    nn.Linear(200,10),#一个将200个节点映射到10个节点的全连接映射。它包含中间隐藏层与输出层10个节点之间所有链接的权重。
    nn.Sigmoid()#再将S型逻辑激活函数应用于10个节点的输出。其结果就是网络的最终输出。也就是我们需要的分类结果。
)
self.loss_function = nn.BCELoss()

震荡很大，这应该与我们每次只遍历一个样本有优化方法有关。不过最后的结果还不错。

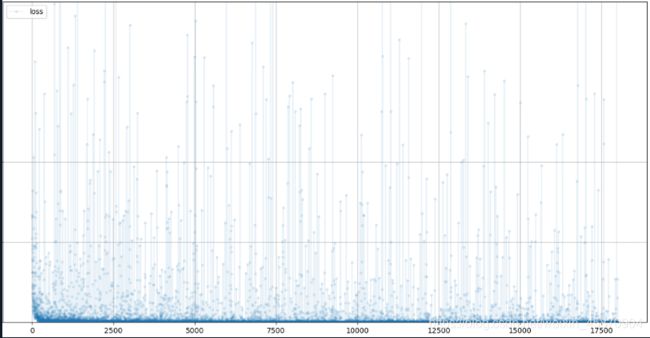
可以看到，0.97可能是这种只有一个隐藏层的全连接神经网络的极限了。要想更高，可能需要重新设计神经网络的结构了。

5.知识点小结(原著版)

1.在使用新的数据或者构建新的流程前，应尽量先通过预览了解数据。这样做可以确保数据被正常载入和交换。
2.pytorch可以替我们完成机器学习中的许多工作。为了充分利用pytorch，我们需要重复使用它的一些功能。比如，神经网络类需要从pytorch的nn.Module父类继承。
3.通过可视化观察损失值，了解训练过程是很推荐的。
4.均方误差损失用于输出是连续值的回归任务；二元交叉熵损失更适合输出是1或0(true/false)的回归任务。
5.传统的S型激活函数在处理较大值时，具有梯度消失的缺点。这在网络训练时会造成反馈信号减弱。ReLu激活函数部分解决了这一问题，保持正值部分良好的梯度值。LeakyReLU进一步改良，在负值部分增加一个很小却不会消失的梯度值。
6.Adam优化器使用动量来避免进入局部最小值，并保持每个可学习参数独立的学习率。在许多任务上，使用它的效果优于SGD优化器。
7.标准化可以稳定神经网络的训练。一个网络的初始权重通常需要标准化。在信号通过一个神经网络时，使用LayerNorm标准化信号值可以提升网络性能。