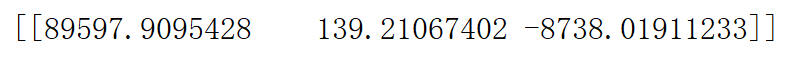机器学习（三）多变量线性回归正规方程解法和梯度下降解法

处理完单变量线性回归的梯度下降解法，跟着黄老师的实验思路，开始处理多变量的线性回归，也有两种解决方式，一种是正规方程，另一种是梯度下降，这篇博客主要是利用这两种思路解决问题。

一、导入库文件

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

二、准备数据集并查看基本信息

面积,房间数,价格
2104,3,399900
1600,3,329900
2400,3,369000
1416,2,232000
3000,4,539900
1985,4,299900
1534,3,314900
1427,3,198999
1380,3,212000
1494,3,242500
1940,4,239999
2000,3,347000
1890,3,329999
4478,5,699900
1268,3,259900
2300,4,449900
1320,2,299900
1236,3,199900
2609,4,499998
3031,4,599000
1767,3,252900
1888,2,255000
1604,3,242900
1962,4,259900
3890,3,573900
1100,3,249900
1458,3,464500
2526,3,469000
2200,3,475000
2637,3,299900
1839,2,349900
1000,1,169900
2040,4,314900
3137,3,579900
1811,4,285900
1437,3,249900
1239,3,229900
2132,4,345000
4215,4,549000
2162,4,287000
1664,2,368500
2238,3,329900
2567,4,314000
1200,3,299000
852,2,179900
1852,4,299900
1203,3,239500

#读入数据集
data = pd.read_csv("mul_data.csv")
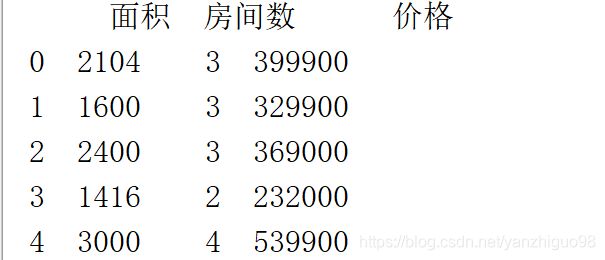
print(data.head())
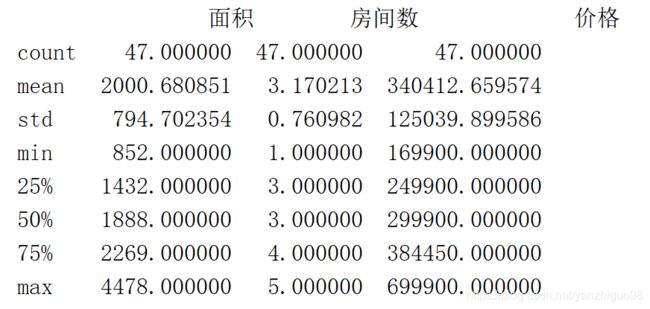
print(data.describe())

  

 

三、构造矩阵

#构造特征矩阵
data.insert(0,'ones',1)
n = data.shape[1]
x = data.iloc[:,:n-1]
y = data.iloc[:,n-1:]
x = np.matrix(x)
y = np.matrix(y)
# w = np.full((1,x.shape[1]),0)

四、图形化数据集

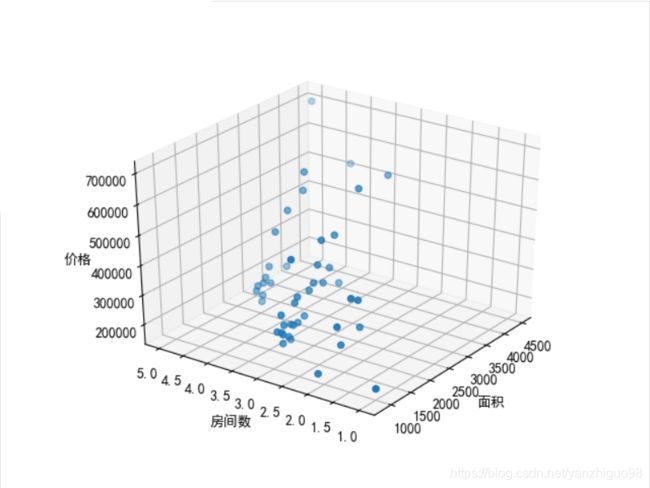
#查看原始数据情况
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(data['面积'],data['房间数'],data['价格'],label = '实际价格')

ax.set_xlabel("面积")
ax.set_ylabel("房间数")
ax.set_zlabel("价格")
plt.show()

五、正规方程求出权重矩阵（没有用特征值归一化求出的权重W）

def normal_function(x,y):
    '''
    利用正规方程解决线性回归问题
    :param x: 特征矩阵
    :param y: 真实值
    :return: 返回权重矩阵
    '''
    return np.linalg.inv(x.T*x)*x.T*y

w = normal_function(x,y).reshape(1,x.shape[1])

 下面是梯度下降

六、梯度下降求出权重矩阵

 

def cost_function(x,y,w):
    '''
    计算代价函数
    :param x: 特征矩阵
    :param y: 真实值矩阵
    :param w: 权重矩阵
    :return: 返回代价函数的值
    '''
    m = x.shape[0]
    return sum(np.power(x*w.T-y,2))/(2*m)
def gradient_descent_function(x,y,w,alpha,iters):
    '''
    梯度下降的函数
    :param x: 特征矩阵
    :param y: 真实值矩阵
    :param w: 权重矩阵
    :param alpha:
    :param iters:
    :return:
    '''
    temp = np.zeros((w.shape[0],w.shape[1]))
    #权重的参数

    w_len = w.shape[1]
    #样本的个数
    x_len = x.shape[0]
    #保存每一次迭代之后代价函数值
    cost = np.zeros(iters)
    for i in range(iters):
        error = x*w.T-y
        for j in range(w_len):
            temp[:,j] = w[:,j] - np.sum(np.multiply(error,x[:,j]))*(alpha/x_len)
        cost[i] = cost_function(x,y,w)
        w = temp
    return w,cost


#对应的步长和迭代次数
alpha = 0.01
iters = 1000
#进行梯度下降
w,cost = gradient_descent_function(x,y,w,alpha,iters)
print(w)

七、注意问题

①：原先我想向单变量一样画出原始散点图和预测曲线，结果发现不行，我的预测曲线是一个平面， 还要继续思考

②：在处理权重矩阵时，一定不要用（5，）数据类型，利用reshape转换成行向量或者是列向量

③：如果不进行特征归一化处理，会造成数据溢出，这是我没有考虑到的地方，上来久开始梯度下降，结果直接报错！又得重新写代码。。。

④：问题：特征值归一化之后影不影响我利用正规方程去求解权重矩阵？

测试：

归一化之后，正规方程求得的结果和梯度下降求得结果大致是一样的

⑤：归一化的函数：

(data-data.mean())data.std()

而我写的就是太片面了

data['房间数'] = (data['房间数']-data['房间数'].mean())/(data['房间数'].std()).astype(float)
data['面积'] = (data['面积']-data['面积'].mean())/(data['面积'].std()).astype(float)
data['价格'] = (data['价格']-data['价格'].mean())/(data['价格'].std()).astype(float)

我还是没有过渡到用矩阵来写代码 ！！！思维没有转变过来。。

⑥：在写梯度下降代码时

 

方式1：temp = np.full((w.shape[0],w.shape[1]),0)
方式2：temp= np.zeros((w.shape[0],w.shape[1]))

结果方式一产生的权重是全0，方式二产生的是正确结果

我又做了测试：

 

发现两种方式产生数组的结果是一样的，但唯一不同的就是数组存放元素的类型，由于方式一存放元素是int型，所以在计算数值时，会发生数值截断，我采取的解决方式如下：

temp = np.full((w.shape[0],w.shape[1]),0).astype(float)

这样就解决了这一BUG 

八、附录代码

（和上面的不一样，切勿直接复制运行，有的代码段被我删除，整体不影响）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
np.set_printoptions(suppress=True)
#读入数据集
data = pd.read_csv("mul_data.csv")
print(data.head())
print(data.describe())



#查看原始数据情况
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(data['面积'],data['房间数'],data['价格'],label = '实际价格')
ax.set_xlabel("面积")
ax.set_ylabel("房间数")
ax.set_zlabel("价格")

# #构造特征矩阵

data['房间数'] = (data['房间数']-data['房间数'].mean())/(data['房间数'].std()).astype(float)
data['面积'] = (data['面积']-data['面积'].mean())/(data['面积'].std()).astype(float)
data['价格'] = (data['价格']-data['价格'].mean())/(data['价格'].std()).astype(float)



data.insert(0,'ones',1)
n = data.shape[1]
x = data.iloc[:,:n-1]
y = data.iloc[:,n-1:]
x = np.matrix(x)
y = np.matrix(y)

#特征值归一化处理
print(data.head())



def normal_function(x,y):
    '''
    利用正规方程解决线性回归问题
    :param x: 特征矩阵
    :param y: 真实值
    :return: 返回权重矩阵
    '''
    return np.linalg.inv(x.T*x)*x.T*y


t = normal_function(x,y).reshape(1,x.shape[1])
print(t)



print('*'*100)
w = np.full((1,x.shape[1]),0)
def cost_function(x,y,w):
    '''
    :param x: 特征矩阵
    :param y: 真实值
    :param w: 特征矩阵对应的权重矩阵
    :return: 返回代价函数的值
    '''
    #总的数据量为m
    m = x.shape[0]
    return np.sum((np.power(x*w.T-y,2)))/(2*m)

def gradient_descent_function(x,y,w,alpha,iters):
    '''
    :param x: 特征
    :param y:真实值
    :param w:权重矩阵
    :param alpha: 步长
    :param iters: 迭代次数
    :return: 返回一个迭代次数对应的代价函数的列表
    '''

    #和w权重矩阵赋值一样
    temp = np.matrix(np.zeros(w.shape))

    #所有的权重参数的数量  w.ravel()变成一维数组 1*n 所以结果是n
    parameters = int(w.shape[1])


    #存入每次迭代之后代价函数的值
    cost = np.zeros(iters)

    #开始迭代
    for i in range(iters):
        #误差值  每一个样本集对应的误差矩阵 n*1
        error = (x * w.T) - y
        for j in range(parameters):
            #每个权重都要修改  x[:, j]代表取所有x的第j个特征
            term = np.multiply(error, x[:, j])
            #更新每一个w[0,j]
            temp[0, j] = w[0, j] - ((alpha / len(x)) * np.sum(term))

        w = temp
        cost[i] = cost_function(x, y, w)
    return w,cost

#对应的步长和迭代次数
alpha = 0.01
iters = 1000
#进行梯度下降
w,cost = gradient_descent_function(x,y,w,alpha,iters)
print(w)